Progressive neural networks Rusu et al, 2016

If you’ve seen one Atari game you’ve seen them all, or at least once you’ve seen enough of them anyway. When we (humans) learn, we don’t start from scratch with every new task or experience, instead we’re able to build on what we already know. And not just for one new task, but the accumulated knowledge across a whole series of experiences is applied to each new task. Nor do we suddenly forget everything we knew before – just because you learn to drive (for example), that doesn’t mean you suddenly become worse at playing chess. But neural networks don’t work like we do. There seem to be three basic scenarios:

• Training starts with a blank slate
• Training starts from a model that has been pre-trained in a similar domain, and the model is then specialised for the target domain (this can be a good tactic when there is lots of data in the pre-training source domain, and not so much in the target domain). In this scenario, the resulting model becomes specialised for the new target domain, but in the process may forget much of what it knew about the source domain (“catastrophic forgetting”).  This scenario is called ‘fine tuning’ by the authors.
• Use pre-trained feature representations (e.g. word vectors) as richer features in some model.

The last case gets closest to knowledge transfer across domains, but can have limited applicability.

This paper introduces progressive networks, a novel model architecture with explicit support for transfer across sequences of tasks. While fine tuning incorporates prior knowledge only at initialization, progressive networks retain a pool of pretrained models throughout training, and learn lateral connections from these to extract useful features for the new task.

The progressive networks idea is actually very easy to understand (somewhat of a relief for someone like myself who is just following along as an interested outsider observing developments in the field!). Some of the key benefits include:

• The ability to incorporate prior knowledge at each layer of the feature hierarchy
• The ability to reuse old computations and learn new ones
• Immunity to catastrophic forgetting

Thus they are a stepping stone towards continual / life-long learning systems.

Here’s how progressive networks work. Start out by training a neural network with some number L of layers to perform the initial task. Call this neural network the initial column of our progressive network:

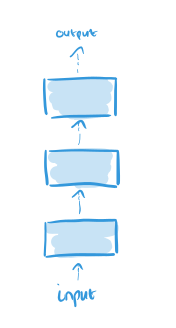
When it comes time to learn the second task, we add an additional column and freeze the weights in the first column (thus catastrophic forgetting, or indeed any kind of forgetting is impossible by design). The outputs of layer l in the original network becomes additional inputs to layer l+1 in the new column.

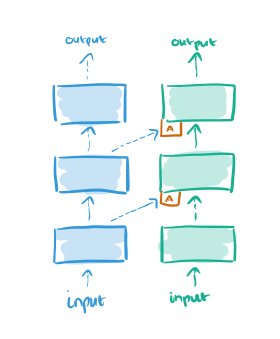
The new column is initialized with random weights.

We make no assumptions about the relationship between tasks, which may in practice be orthogonal or even adversarial. While the fine tuning stage could potentially unlearn these features, this may prove difficult. Progressive networks side-step this issue by allocating a new column for each task, whose weights are initialized randomly.

Suppose we now want to learn a third task. Just add a third column, and connect the outputs of layer l in all previous columns to the inputs of layer l+1 in the new column:

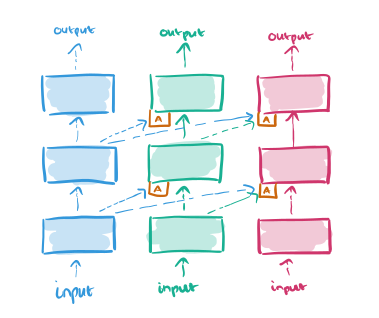
This input connection is made through an adapter which helps to improve initial conditioning and also deals with the dimensionality explosion that would happen as more and more columns are added:

…we replace the linear lateral connection with a single hidden layer MLP (multi-layer perceptron). Before feeding the lateral activations into the MLP, we multiply them by a learned scalar, initialized by a random small value. Its role is to adjust for the different scales of the different inputs. The hidden layer on the non-linear adapter is a projection onto an n_l dimensional subspace (n_l is the number of units at layer _l).

As more tasks are added, this ensures that the number of parameters coming from the lateral connections remains in the same order.

Progressive networks in practice

The evaluation uses the A3C framework that we looked at yesterday. It’s superior convergence speed and ability to train on CPUs made it a natural fit for the large number of sequential experiments required for the evaluation.  To see how well progressive networks performed, the authors compared both two and three-column progressive networks against four different baselines:

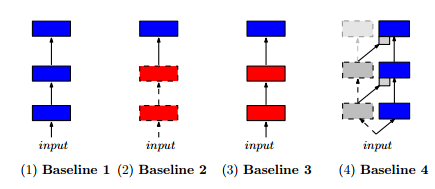
• (i) A single column trained on the target task (traditional network learning from scratch)
• (ii) A single column, using a model pre-trained on a source task, and then allowing just the final layer to be fine tuned to fit the target task
• (iii) A single column, using a model pre-trained on a source task, and then allowing the whole model to be fine tuned to fit the target task
• (iv) A two-column progressive network, but where the first column is simply initialized with random weights and then frozen.

The experiments include:

• Learning to play the Atari pong game as the initial task, and then trying to learn to play a variety of synthetic variants (extra noise added to the inputs, change the background colour, scale and translate the input, flip horizontally or vertically).
• Learning three source games (three columns, one each for Pong, RiverRaid, and Seaquest) and then seeing how easy it is to learn a new game – for a variety of randomly selected target games.
• Playing the Labyrinth 3D maze game – each column is a level (track) in the game, and we see how the network learns new mazes using information from prior mazes.

For the Pong challenge, baseline 3 (fine tuning a network pre-trained on Pong prior to the synthetic change) performed the best of the baselines, with high positive transfer. The progressive network outperformed even this baseline though, with better mean and median scores.

As the mean is more sensitive to outliers, this suggests that progressive networks are better able to exploit transfer when transfer is possible (i.e. when source and target domains are compatible).

For the game transfer challenge the target games experimented with include Alien, Asterix, Boxing, Centipede, Gopher, Hero, James Bond, Krull, Robotank, Road Runner, Star Gunner, and Wizard of Wor.

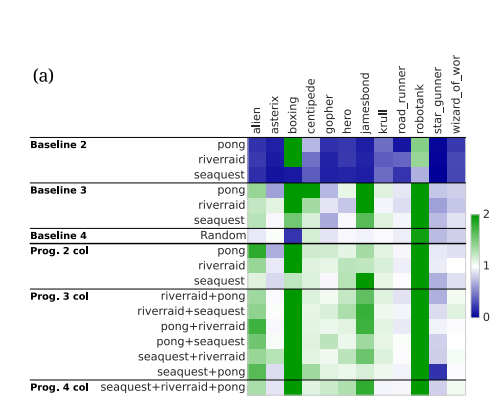
Across all games, we observe that progressive nets result in positive transfer in 8 out of 12 target tasks, with only two cases of negative transfer. This compares favourably to baseline 3, which yields positive transfer in only 5 out of 12 games.

The more columns (the more prior games the progressive network has seen), the more progressive networks outperform baseline 3.

Seaquest -> Gopher (two quite different games) is an example of negative transfer:

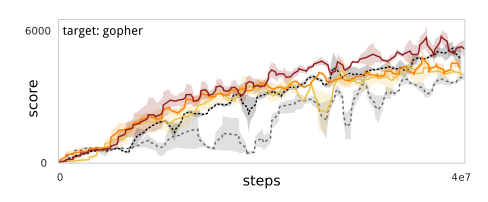
Sequest -> RiverRaid -> Pong -> Boxing is an example where the progressive networks yield significant transfer increase.

With the Labyrinth tests, the progressive networks once again yield more positive transfer than any of the baselines.

Limitations and future directions

Progressive networks are a stepping stone towards a full continual learning agent: they contain the necessary ingredients to learn multiple tasks, in sequence, while enabling transfer and being immune to catastrophic forgetting. A downside of the approach is the growth in number of parameters with the number of tasks. The analysis of Appendix 2 reveals that only a fraction of the new capacity is actually utilized, and that this trend increases with more columns. This suggests that growth can be addressed, e.g. by adding fewer layers or less capacity, by pruning [9], or by online compression [17] during learning. Furthermore, while progressive networks retain the ability to solve all K tasks at test time, choosing which column to use for inference requires knowledge of the task label. These issues are left as future work.

The other observation I would make is that the freezing prior columns certainly prevents catastrophic forgetting, but also prevents any ‘skills’ a network learns on subsequent tasks being used to improve performance on previous tasks. It would be interesting to see backwards transfer as well, and what could be done there without catastrophic forgetting.