Flexible Paxos: Quorum intersection revisited Howard et al., 2016
Paxos has been around for 18 (26) years now, and extensively studied. (For some background, see the 2 week mini-series on consensus that I put together last year). In this paper, Howard et al. make a simple(?) observation that has significant consequences for improving the fault-tolerance and throughput of Paxos-based systems. After so much time and so much study, you can’t help but admire that.
Paxos proceeds in two phases: in the first phase a proposer is chosen (through a quorum), known as the leader; in the second phase the leader proposes a value to be agreed upon by the participants (acceptors) and brings a quorum to agreement. Paxos (like many other consensus systems) uses majority agreement for its quorums (i.e., at least N/2 + 1 out of N acceptors), which guarantees an intersection between the participants in phase one and phase two. Since we normally want to make agreement over a series of values (referred to in the literature as slots), we need to run a distinct instance of Paxos each time. Multi-Paxos recognises that the first phase (leader election) is independent of the proposal phase, so why not do that once and then retain that leader through a whole series of phase two agreements?
Here’s the key new insight: Paxos is more conservative than necessary in requiring a majority quorum in each phase. All we actually need to guarantee is that the phase one and phase two quorums intersect. We don’t need to guarantee that phase one quorums across successive rounds intersect, nor that phase two quorums intersect. If Q1 represents the participants in the first phase quorum, and Q2 the participants in the second phase quorum, then |Q1| + |Q2| > N (for N overall participants) will provid the needed guarantee. And that gets really interesting when you consider that (hopefully) leader elections happen much less frequently than phase 2 slot-decisions. So you can trade off e.g. requiring a larger quorum when you do need to elect a new leader for having a smaller quorum requirement during regular operations. The authors call this variant Flexible Paxos (FPaxos). If you’re like me, you’ll want to see some kind of proof or justification for the quorum intersection claim – I spent the first 8 pages of the paper hungry for it! It’s in section 5 starting on page 9. There’s also a model checked formal specification in TLA+ in the appendix.
In this paper, we demonstrate that Paxos, which lies at the foundation of many production systems, is conservative. Specifically, we observe that each of the phases of Paxos may use non-intersecting quorums. Majority quorums are not necessary as intersection is required only across phases.
It has previously been noted that Paxos could be generalized to replace majority quorums with any quorum system guaranteeing any two quorums will have a non-empty intersection. FPaxos takes this generalisation one step further by relaxing the conditions under which such guarantees are needed in the first place.
Howard et al. (to the best of their knowledge) are the first to prove and implement the generalization. While preparing their publication Sougoumarane independently made the same observation on which the work is based, and released a blog post summarising it last month.
Why does all this matter?
The fundamental theorem of quorum intersection states that [the resilience of a quorum system] is inversely proportional to the load on (hence the throughput of) the participants. Therefore, with Paxos and its intersecting quorums, one can only hope to increase throughput by reducing the resilience, or vice versa…. by weakening the quorum intersection requirement, we can break away from the inherent trade off between resilience and performance.
Howard et al. go on to illustrate the practical implications of the relaxed quorum requirement for FPaxos using majority quorums, simple quorums, and grid quorums. These however can be considered “naive” quorum systems, and FPaxos actually opens up a whole new world:
There already exists an extensive literature on quorum systems from the fields of databases and data replication, which can now be more efficiently applied to the field of consensus. Interesting example systems include weighted voting, hierarchies, and crumbling walls.
[And that’s another addition to my known unknowns list ;) ].
Majority quorums
If we stick with majority quorums, FPaxos allows us to make a simple improvement in the case when the number of acceptors n is even. Instead of needing n/2 +1 participants in Q2, we can reduce this to n/2.
Such a change would be trivial to implement and by reducing the number of acceptors required to participate in replication, we can reduce latency and improve throughput. Furthermore, we have also improved the fault tolerance of the system. As with Paxos, if at most n/2 -1 failures occur then we are guaranteed to be able to make progress. However unlike with Paxos, if exactly n/2 acceptors fails and the leader is still up then we are able to continue to make progress and suffer no loss of availability.
Simple quorums
Simple quorums are for me the most natural way of understanding the benefits of FPaxos. “We will use the term simple quorums to refer to a quorum system where any acceptor is able to participate in a quorum and each acceptor’s participation is counted equally. Simple quorums are a straightforward generalization of majority quorums.”
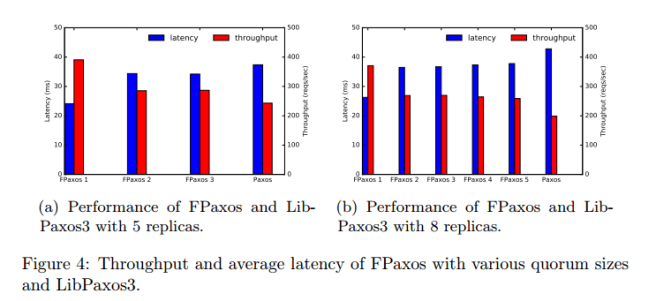
Since we require only that |Q1| + |Q2| > N, and we know that phase 2 happens a lot more often than phase one, we can reduce the quorum size requirement in phase 2 and make a corresponding increase in phase 1. Take a classic Paxos deployment with 5 replicas. Whereas traditionally each phase requires at least three nodes (acceptors) to be up, we can tweak this to require four acceptors in a leader election quorum, but only two acceptors for Q2.
FPaxos will always be able to handle up to |Q2| – 1 failures. However, if between |Q2| to N – |Q2| failures occur, we can continue replication until a new leader is required.
If we chose 5 replicas with |Q1| = 4 and |Q2| = 2, we therefore will always be able to handle any single failure, and we’ll be able to continue replication with the loss of up to three replicas, so long as we don’t need a new leader.
Here are some results from the evaluation showing how the latency and throughput of FPaxos compares to regular Paxos with varying Q2 quorum sizes:
Grid quorums
Grid quorum schemes arrange the N nodes into a matrix of N1 columns by N2 rows, where N1 × N2 = N and quorums are composed of rows and columns. As with many other quorum systems, grid quorums restrict which combinations of acceptors can form valid quorums. This restriction allows us to reduce the size of quorums whilst still ensuring that they intersect.
Whereas with simple quorums any reduction in |Q2| must be paid for by a corresponding increase in |Q1|, with grid quorums we can make different trade-offs between quorum size, quorum selection flexibility, and fault tolerance.
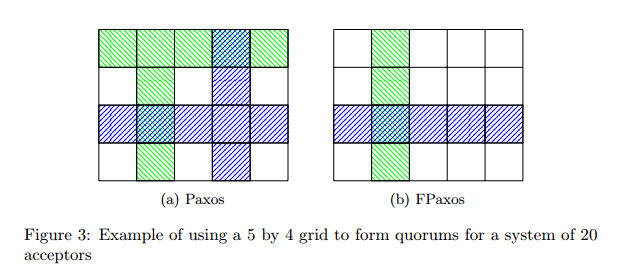
Since Paxos requires all quorums to intersect, one suitable scheme would be to require one row and one column to form a quorum : (a) in the figure above.
In FPaxos we can safely reduce our quorums to one row of size N1 for Q1, and one column of size N2 for Q2. This construction is interesting as quorums from the same phase will never intersect, and may be useful in practice for evenly distributing the load of FPaxos across a group of acceptors.
A further enhancement
FPaxos only requires that a given Q1 will intersect with all Q2’s with lower proposal numbers. Given a mechanism to learn which Q2s have participated in lower numbered proposals, we have further flexibility in choosing a Q1 quorum.
The implications of this enhancement can be far reaching. For example, in a system of N = 100 f nodes, a leader may start by announcing a fixed Q2 of size f+1 and all higher proposal numbers (and readers) will need to intersect with only this Q2. This allows us to tolerate _N-f_failures…
(And many other interesting variations are possible).
The bottom line
Generalizing existing systems to use FPaxos should be quite straightforward. Exposing replication (phase 2) quorum size to developers would allow them to choose their own trade-off between failure tolerance and steady state latency… [Secondly], by no longer requiring replication quorums to intersect, we have removed an important limit on scalability. Through smart quorum construction and pragmatic system design, we believe a new breed of scalable, resilient, and performant consensus algorithms is now possible.
6 thoughts on “Flexible Paxos: Quorum intersection revisited”
Comments are closed.