Time evolving graph processing at scale Iyer et al., GRADES 2016

Here’s a new (June 2016) paper from the distinguished AMPlab group at Berkeley that really gave me cause to reflect. The work addresses the problem of performing graph computations on graphs that are constantly changing (because updates flow in, such as a new follower in a social graph). Many graphs of interest have this property of constantly evolving. In part, that’s what makes them interesting. You could always take a snapshot of e.g. the graph as it was at the end of the previous day and compute on that, but some applications need more up to date results (e.g. detecting traffic hotspots in cellular networks), and many applications would benefit from real-time results. GraphTau is a solution to this problem, implemented on top of GraphX which is in turn implemented on top of Spark’s RDDs. It’s a convergence of stream processing and graph processing.

I’m seeing a lot of streaming recently, and a lot of convergence. That topic probably warrants a separate post. In the meantime…

Graph-structured data is on the rise, in size, complexity and the dynamism they exhibit. From social networks to telecommunication networks, applications that generate graph-structured data are ubiquitous… the dynamic nature of these datasets gives them a unique characteristic – the graph-structure underlying the data evolves over time. Unbounded, real-time data is fast becoming the norm, and thus it is important to process these time-evolving graph-structured datasets efficiently.

(Aside: applications generating graph-structured data certainly are ubiquitous – pretty much any relational database has graph structure the minute you introduce foreign keys. It’s applications generating graph-structured data and that require extensive traversals or graph-specific computations that we’re really interested in here).

For time-evolving graph-structured datasets, the authors identify three core requirements:

1. The ability to execute iterative graph algorithms in real-time
2. The ability to combine graph-structured data with unstructured and tabular data
3. The ability to run analytics over windows of input data

While some specialized systems for evolving-graph processing exist, these do not support the second and third requirements.  GraphTau is “the first time-evolving graph processing system, to our knowledge, built on a general purpose dataflow framework.” GraphTau is built on top of GraphX, which maintains graphs internally as a pair of RDDs: a vertex collection and an edge collection.

(Note that Apache Flink has Gelly, which builds graph processing on top of a streaming dataflow core, but does not support iterative processing over evolving graphs to the best of my knowledge.)

The main idea in GraphTau is to treat time-evolving graphs as a series of consistent graph snapshots, and dynamic graph computations as a series of deterministic batch computations on discrete time intervals. A graph snapshot is simply a regular graph, stored as two RDDs, the vertex RDD and the edge RDD. We define GraphStream as a sequence of immutable, partitioned datasets (graphs represented as two RDDs) that can be acted on by deterministic operators. User programs manipulate GraphStreams to produce new GraphStreams, as well as intermediate state in the form of RDDs or graphs.

A DeltaRDD is an RDD whose elements are updates that need to be applied to a graph. A stream of such updates is called a DeltaDStream.  GraphStreams can be built from a DeltaDStream or directly from a vertex DStream and an edge DStream.

There are two supported computational models, called pause-shift-resume and online rectification.

Pause-shift-resume

Some classes of graph algorithms can cope with the graph being modified while the algorithm is still converging. For example, if a graph changes during an evaluation of PageRank you’ll still get an answer, which studies have shown will be within a reasonable error to the actual answer you’d get if you started the algorithm again from scratch with the now current graph.

Under these conditions, the pause-shift-resume (PSR) model is appropriate.

In this model, GraphTau starts running a graph algorithm as soon as the first snapshot of a graph is available. Upon the availability of a new snapshot, it pauses the computation on the current graph, shifts the algorithm specific data to the new snapshot, and resumes the computation on the new graph.

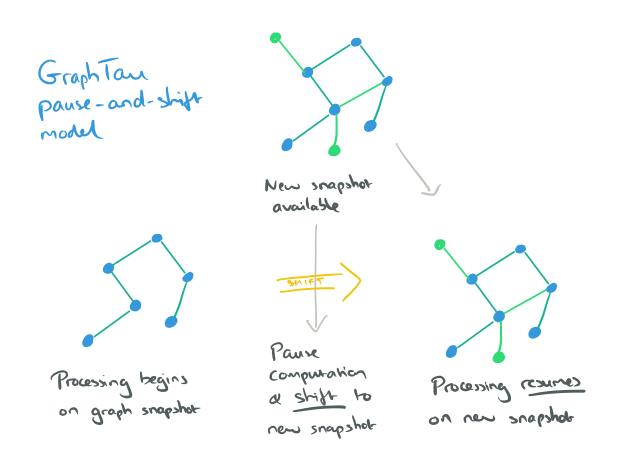
Online rectification

Algorithms such as connected-components will produce incorrect results under the PSR model (consider an edge or vertex that is removed during processing).

For such algorithms, GraphTau proposes the online rectification model. In this model, GraphTau rectifies the errors caused by the underlying graph modificationts in an online fashion using minimal state.

In the connected component example, it is necessary for every vertex to keep track of its component id over time. The approach works for any algorithm based on label propagation, at the expense of needing to keep algorithm-specific state.

The question of time

GraphStream splits time into non-overlapping intervals, and stores all the inputs received during these intervals in batches (worker nodes are synchronized using NTP).  Such intervals are based on receive time, there is also an option to process based on external timestamps (event time) which requires either the introduction of limited slack time to wait for late events, or application specific code to correct for late records.

Each interval’s updates reflects all of the input received until then. This is despite the fact that the DeltaRDD and its updated graph snapshot are distributed across nodes. As long as we process the whole batch consistently (e.g. ordered by timestamps), we will get a consistent snapshot. This makes distributed state much easier to reason about and is the same as “exactly once” processing of the graph updates even with faults or stragglers.

GraphStream inherits its recovery mechanisms from GraphX and its RDDs: parallel recovery of lost state and speculative execution.

Programming with GraphTau

The GraphStream interface supports transform, merge, streamingBSP, and forEachGraph operations as well an updateLocalState operator to allow for event processing and state tracking.

• mergeByWindow merges all graphs from a sliding window of past time intervals into one graph
• forEachGraph applies a function to each graph generated from the GraphStream
• transformWith combines two graph streams with various join and cogroup operators.
• the streamingBSP operator supports differential computation

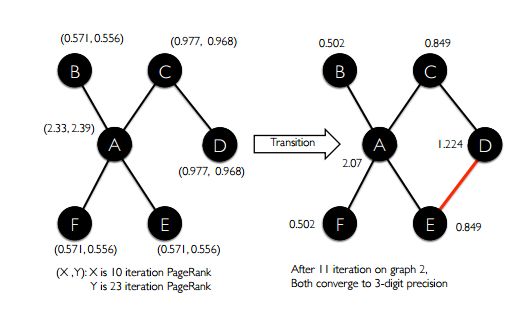
This [streamingBSP] operator enables efficient implementation of a large class of incremental algorithms on time-evolving graphs. We signal the availability of the new graph snapshot using a variable in the driver program. In each iteration of Pregel, we check whether a new graph is available. If so, we do not proceed to the next iteration on the current graph. Instead, we resume computation on the new graph reusing the result, where only vertices in the new active set continue message passing. The new active set is a function of the old active set and the changes between the new graph and the old graph. For a large class of algorithms (e.g. incremental PageRank), the new active set includes vertices from the old set, any new vertices, and vertices with edge additions and deletions.

Here’s what the Page Rank example looks like:

Even on a simple six-node graph where one edge is added after 10 iterations, this saves 13/34 iterations overall.

Here’s another example GraphTau program, showing the ability to unify data and graph stream processing.

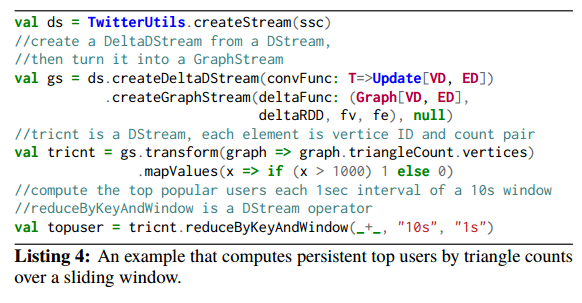
This example computes top users in terms of triangle counts from a Twitter attention graph. A DStream ds is created from the external Twitter feed, and then a GraphStream is built from it. Triangle count is applied to each graph snapshot, and then we compute the number of times a user is a top user over a sliding window of ten seconds, outputting results every second.

Preliminary evaluation shows that GraphTau’s performances matches or exceeds that of specialized systems on a streaming connected components task based on a cellular dataset.

The last word…

In this paper, we presented GraphTau, a time-evolving graph processing system built on a data flow framework that addresses this demand. GraphTau represents time-evolving graphs as a series of consistent graph snapshots. On these snapshots, GraphTau enables two computational model, the Pause-Shift-Resume model and the Online Rectification model which allows the application of differential computation on a wide variety of graph algorithms. These techniques enable GraphTau to achieve significant performance improvements.