Spheres of influence for more effective viral marketing Mehmood et al. SIGMOD ’16
In viral marketing the idea is to spread awareness of a brand or campaign by exploiting pre-existing social networks. The received wisdom is that by targeting a few influential individuals, they will be able to spread your marketing message to a large portion of the network. The Influence Maximization problem involves finding the set of k nodes (the ‘seed set’) such that activating these nodes maximizes the eventual reach. But Duncan Watts challenged this hypotheses ("Challenging the influentials hypothesis, Watts 2007), stating that influence processes are highly unreliable, and therefore it is better to target a large seed of ordinary individuals, each with a smaller but more reliable sphere of influence.
Inspired by this vision, in this paper we study how to compute the sphere of influence of each node s in the network, together with a measure of stability of such sphere of influence, representing how predictable the cascades generated from s are. We then devise an approach to influence maximization based on the spheres of influence and maximum coverage, which is shown to outperform in quality the theoretically optimal method for influence maximization when the number of seeds grows.
The standard algorithm for influence maximisation is a greedy one, and the solution outlined in this paper is the first (to the best of the author’s knowledge) to show a consistent improvement over it.
The Typical Cascade problem
Imagine a probabilistic directed graph, where each edge has an associated probability that it will participate in a contagion cascade. We’d like to know what set of nodes C are likely to be reached from some source node s. In addition to viral marketing applications, you can imagine this information being using in studying epidemics, failure propogation in financial and computer networks, and other related areas.
Given the probabilistic nature, what set C should be returned from such a query?
One could think to select the most probable cascade, but this would not be a good choice as explained next. If we have |V| = n nodes there are 2n possible cascades and n is usually large. This means that we have a probability distribution over a very large discrete domain, with all the probabilities that are very small. As a consequence the most probable cascade still has a tiny probability, not much larger than many other cascades. Finally, the most probable cascade might be very different from many other equally probable cascades.
So instead, the authors are interested in the typical cascade : the set of nodes which is closest in expectation to all the possible cascades of s. If we want to talk about how “close” one set of nodes is to another set, we’ll need some way of defining the distance between them. For this purpose, the Jaccard Distance is used. The Jaccard Distance of two sets A and B is the number of elements that appear only in A or only in B, divided by the total number of elements in A and B:
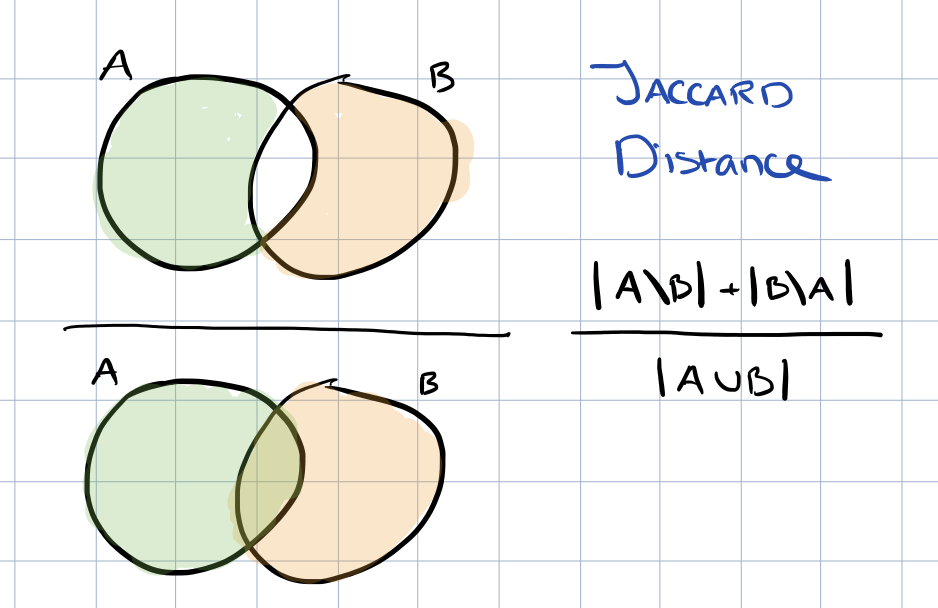
The goal is to find the set of nodes that minimizes the summed expected cost to all of the random cascades from s. This set represents the typical cascade of the node s, or its sphere of influence. The smaller the distance the greater the stability (i.e. random cascades from s deviate less from the typical cascade).
So far so good. Unfortunately… “computing the expected cost of a set of nodes (a typical cascade) is #P-hard.” (The authors provide a proof, but here I’m prepared to take their word for it). The closely related problem: given the set of all cascades from s, find their Jaccard Median, also turns out to be NP-hard, although there is a known polynomial time approximation scheme.
A natural approach to deal with some #P-hard problems is by means of Monte-Carlo sampling…
So here’s what we can do:
- Sample l random cascades from a source node s, and
- Compute the Jaccard median of this smaller set of cascades, as the typical cascade
But how many random cascades do we need in our sample in order to have confidence in the results? The surprising result, is that independent of n (the number of nodes in the graph), a sample size of log(1/α)/α2 is sufficient to obtain an (1+O(α))-approximate median. (“A 1-median in a finite metric space is a point with the minimum average distance to all other points,” – Some results on approximate 1-median selection in metric spaces). The proof of this is in section 3 of the paper.
Practical algorithms for the Typical Cascade problem
We have two sub-problems to solve: firstly, efficiently creating a set of l = O(log(1/α)/α2 samples; and secondly computing their approximate Jaccard median once we have them. For the second problem, the authors defer to the work of Chierichetti et al. (“Finding the Jaccard median”) using the algorithm described in section 3.2 of their paper (a polynomial time approximation).
That leaves us with the problem of efficiently computing the set of cascades. This is addressed by sampling l ‘possible worlds’ Gi…Gl from the graph G, each of which implicitly defines a sample cascade from a vertex v ∈ G.
A key observation that we exploit to speed up this process is that all the vertices in the same strongly connected component (SCC) have the same reachability set: since any two vertices u, v in the same SCC are reachable from each other, any vertex reachable by u is also reachable by v, and viceversa. Therefore we can represent each sampled possible world Gi by its SCC structure. Representing Gi in terms of its SCCs yields savings in both space usage and computational runtime, because of the compactness of representation and because a single depth first search is sufficient to identify the reachability set of all vertices in the same component.
Based on this idea an index containing information about the links between SCCs, denoted Ci (obtained by contracting each component of the graph to a single vertex), and a mapping from vertex to connected component, is constructed. Then, …
Given a node v and i ∈ [l], the cascade of v in Gi can be obtained as follows: look at the identifier of the SCC of v in Gi; recursively follow the links from the associated condensed vertex in Ci to find all the reachable components; and output the union of the elements in the reachable components. The time to perform this computation is linear in the number of nodes of the output and the number of edges of the condensation Ci, which is typically much smaller than the number of edges of Gi.
Application to influence maximisation
Given typical cascades (computed as above) for all vertices in a graph, we can use a standard greedy algorithm that runs for k iterations. Let the set of ‘covered nodes’ be the union of all the nodes in the typical cascades of the chosen seed nodes so far. At each iteration, the algorithm simply choses the node which increases the size of the the ‘covered nodes’ set the most.
… our main practical result: the fact that our method for influence maximization based on spheres of influence outperforms the standard influence maximization method for what concerns quality, i.e., the the expected spread achieved.
(See figure 6 in the paper for a series of charts demonstrating this).
Why does the greedy algorithm based on typical cascades beat the standard greedy algorithm, which is based on chosing the node with the maximum expected spread at each stage? The answer is that the standard algorithm saturates earlier (that is, finds it harder to detect meaningful differences amongst the remaining choices). “… our method has more power to discriminate among interesting nodes, as it reaches the saturation point much later.”
This was a pretty meaty paper for a Friday, and I had to work hard to follow parts of it. I hope I have at least managed to convey the essence of the idea.
In reading around the topic a little bit, I also came across ‘Measuring influence in Twitter: the million follower fallacy’ (Cha et al. 2010), and ‘Who creates trends in online social media: the crowd or opinion leaders?’ (Zhang et al. 2014). Short version: you maximise your own influence by keeping your tweets to a well-defined topic area; and early participation of the crowd (not just a small number of influencers) is important for eventual large-scale coverage.