Delta State Replicated Data Types – Almeida et al. 2016

You know when you want to use CRDTs for their convergence properties, but the amount of state you’re required to pass around gets out of hand? In this paper, Almeida et al. show how to retain the advantages of state-based CRDTs, but with much smaller state deltas being exchanged as opposed to the full state. On top of this mechanism, they build a portfolio of Delta State CRDTs.

State-based CRDTs are generally preferred to their operation-based cousins since they don’t assume a messaging layer with reliable exactly-once causal broadcast: “these guarantees are hard to maintain since large logs must be retained to prevent duplication even if TCP is used…”.

However, a major drawback in current state-based CRDTs is the communication overhead of shipping the entire state, which can get very large in size. For instance, the size of a counter CRDT (a vector of integer counters, one per replica) increases with the number of replicas; whereas in a grow-only Set, the state size depends on the set size, that grows as more operations are invoked.

Instead of shipping the full state, ideally we would like to ship some kind of a delta that can be applied at replicas – all the while preserving all of the benefits of CRDTs of course.

The challenge in δ-CRDT is that individual deltas are now “state fragments” and usually must be causally merged to maintain the desired semantics. This raises the following questions: is merging deltas semantically equivalent to merging entire states in CRDTs? If not, what are the sufficient conditions to make this true in general? And under what constraints is causal consistency maintained? This paper answers these questions and presents corresponding proofs and examples.

Let’s start with an example. The GCounter is a state-based increment-only counter. Its state is a map from replica identifiers to positive integers, and the initial bottom (⊥) state is just the empty map. When a given replica increments the counter, it simply updates the element in the map that corresponds with its Id. To calculate the value of the counter, we simply sum the counts for each replica in the map. To join two states, we combine the two maps, retaining the higher value in the case that both maps have an entry for the same key. When updates are disseminated, the full state is sent.

The δ-CRDT equivalent of the GCounter uses exactly the same state (the map from replica ids to counter values), join operation, and query operation to obtain the counter value. Whereas the inc operation in the original GCounter retains a whole new map to be disseminated though, the inc operation in the δ-CRDT implementation just returns the updated entry (strictly, a map containing just the replication id → new counter value entry). This delta can be disseminated as before, and following the join protocol its easy to see that all replicas will end up with the same state as in the original (full) state-based implementation.

Here it can be noticed that… a delta is just a state, that can be joined possibly several times without requiring exactly-once deliver, and without being a representation of the “increment” operation (as in operation-based CRDTs), which is itself idempotent.

We can also join several deltas together locally into a delta-group (i.e., coalesce several local increment operations into a single state update). Disseminating delta-groups at a lower rate than the operation rate reduces data communication overhead as you can collapse multiple operations into a single update.

A traditional state-based CRDT is defined as a triple (S,M,Q) where S is a join-semi-lattice; M is a set of mutators that perform updates with each m ∈ M taking a state X ∈ S and returning a new state X’ = m(X); and Q is the set of query functions, which return some result without modifying the state.

A δ-CRDT (S,M^δ,Q) is a delta-state decomposition of a state-based CRDT (S,M,Q), if for every mutator m ∈ M, we have a corresponding mutator m^δ ∈ M^δ such that, for every state X ∈ S: m(X) = X join m^δ(X).

State convergence in δ-CRDTs is achieved if all delta-mutations generated in the system eventually reach every replica…

This opens up the possibility of having anti-entropy algorithms that are only devoted to enforce convergence, without necessarily providing causal consistency (enforced in standard CRDTs); thus making a trade-off between performance and consistency guarantees.

But what if you do want the causal consistency guarantees? We would need to constrain the delta propagation and merging in such a manner as to give the same results as if a standard CRDT was used. It turns out that…

Any δ-CRDT in which states are propagated and joined using a delta-interval-based anti-entropy algorthim satisfying the causal delta-merging condition ensures causal consistency.

To unpack this, we need to understand what a delta-interval is; what a delta-inverval based anti-entropy algorithm is; and what the causal delta-merging condition is.

A delta-interval is very straightforward. Consider some replica i progressing through states X_i^k,X_i^k+1, … by joining delta d_i^k,d_i^k+1 and so on, where each delta may be either a local mutation or one received from another replica. A delta-interval Δ_i^a,b is simply what we get if we take all of the deltas from δ_i^a to δ_i^b-1 and join them together.

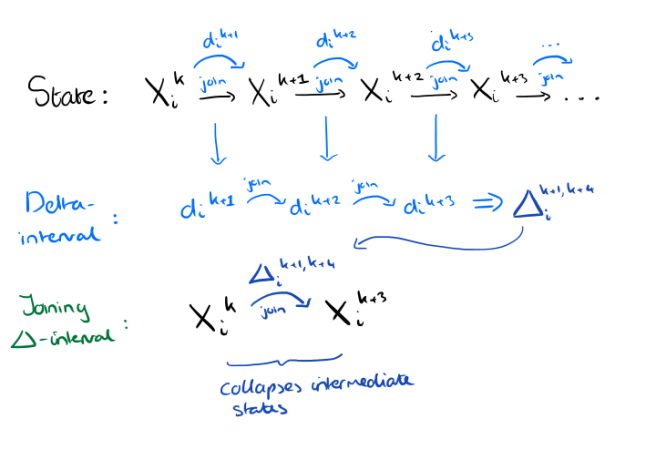
A delta-interval based anti-entropy algorithm is simply one in which all deltas sent to other replicas are delta-intervals.

Finally, the causal delta-merging condition says that a delta interval Δ_j^a,b from replica j can only be joined into the state X_i of replica i if X_i is partially ordered after X_j^a in the join-semi-lattice.

This means that a delta-interval is only joined into states that at least reflect (i.e. subsume) the state into which the first delta in the interval was previously joined.

Section 6 of the paper describes an an anti-entropy algorithm which enforces this condition. I’ll refer you to the paper for details of that, and instead finish up with a look at the portfolio of δ-CRDTs the paper concludes with.

A δ-CRDT portfolio

Although we cover a significant number of CRDTs , the goal is not to provide an exhaustive survey, but instead to illustrate more extensively the design of specifications with deltas.

Two common operations that are used to join states in these CRDTs are Pair composition and Lexicographic Pair composition. Pair composition is a straightforward coordinate-wise join of the components. In lexicographic pair composition, the first element takes priority in establishing the outcome of the join (whichever element has the greatest first element wins), and in the event of a tie the second element is used to compare.

Building on this, the authors show three categories of δ-CRDTs with increasing complexity: anonymous δ-CRDTs, which do not require replica identifiers; named δ-CRDTs, which do use replica identifiers to partition the state; and causal δ-CRDTs which use causal history (a causal context).

A trivial example of an anonymous δ-CRDT is a GSet (grow-only set), where the delta is simply a singleton set containing the element to be added. This can be extended into a 2PSet (two-phase set) supporting add and remove by pairing two grow-only sets in the normal manner. The paper also contains an example of an Add-Wins Last-Writer-Wins Set that keeps timestamps for elements in the Set together with a boolean flag indicating whether the element is included or not.

A dual construction to the Add-Wins LWW Set is a Remove-Wins LWW Set, where remove operations take priority on the event of a timestamp tie. This construction has been widely deployed in production as part of the SoundCloud system.

An example of a named δ-CRDT is a positive-negative counter (PNCounter) that can track both increments and decrements. This is formed by combining two grow-only δ-CRDTs, one for increments, and one for decrements.

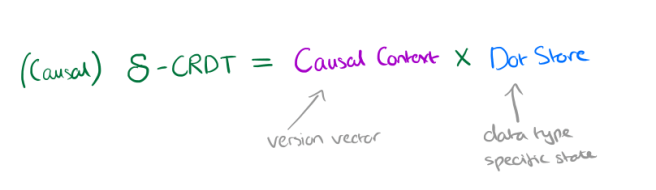
Causal CRDTs use version vectors to keep track of versions across replicas:

A common property to causal CRDTs is that events can be assigned unique identifiers. A simple mechanism is to create these identifiers by appending to a globally unique replica identifier a replica-unique integer. For instance, in replica i ∈ Id we can create the sequence (i,1),(i,2),… Each of these pairs can be used to tag a specific event, or client action, and if we collect these pairs in a grow-only set, we can remember which events are known to each replica. The pair is called a dot and the grow-only set of pairs can be called a causal history, or alternatively a causal context, as we do here.

A Causal Context is therefore just a set of dots. Let max_i(c) give the maximum sequence number in the context c for replica i (or 0), and next_i(c) produce the next available sequence number for replica i given the set of elements in c.

Under causal consistency, the causal context can always be encoded as a compact version vector Id → ℕ that keeps the maximum sequence number for each replica.

In conjunction with the causal context version vector, a causal CRDT keeps the actual datatype specific state in a Dot Store….

A dot store can be queried about the set of event identifiers (dots) corresponding to the relevant operations in the container, by the function dots, which takes a dot store and returns a set of dots.

Depending on the CRDT in question, the dot store may be a simple set, a map from dots to some lattice, or the most generic DotMap(K,V) which maps some set K to to values which are themselves dot stores;

To understand the meaning of a state (and the way join must behave), a dot present in a causal context but not in the corresponding dot store, means that the dot was present in the dot store some time in the past, but has been removed meanwhile. Therefore, the causal context can track operations with remove semantics, while avoiding the need for individual tombstones. When joining two replicas, a dot present in only one dot store, but included in the causal context of the other, will be discarded. This is clear for the simpler case of a DotSet, where the join preserves all dots in common, together with those not present in the other causal context.

The full rules are given below:

Here’s a worked example for a DotSet that helped me get all this straight in my head…

Perhaps the simplest causal CRDT is an Enable-Wins Flag, “a simple yet useful data-type first introduced in Riak 2.0.” As the name suggests, this is a flag that favours enable over disable in the event of concurrent modification.

Enabling the flag simply replaces all dots in the store by a new dot; this is achieved by obtaining the dot through next_i(c), and making the delta mutator return a store containing just the new dot, together with a causal context containing both the new dot and all current dots in the store; this will cause all current dots to be removed from the store upon a join (as previously defined), while the new dot is added.

The paper also contains examples of multi-value registers, add-wins sets, and remove-wins sets.

The grand concluding example in the paper is “Map Embedding Causal δ-CRDTs:”

Riak 2.0 introduced a map design that provides a clear observed-remove semantics: a remove can be seen as an “undo” of all operations leading to the embedded value, putting it in the bottom state, but remembering those operations, to undo them in other replicas which observe it by a join. Key to the design is to enable removal of keys to affect (and remember) the dots in the associated nested CRDT, to allow joining with replicas that have concurrently evolved from the before-removal point, or to ensure that re-creating entries previously removed does not introduce anomalies.

The key thing here is that you can’t just have a regular map where each entry has its own causal context. Suppose an entry in the map is removed, and later recreated. When recreated it will start again at the bottom (⊥) state meaning that at another replica which had not yet processed the original remove, we may consider the (out of date) old entry to be more recent.

For an arbitrary set of keys K and a causal δ-CRDT Causal<V> that we want to embed (including, recursively, the map we are defining), the desired map can be achieved through Causal<DotMap<<K,V>>, where a single causal context is shared by all keys and corresponding nested CRDTs. This map can embed any causal CRDTs as values.

The map doesn't have a special operation to add new entries, it starts as an empty map which corresponds to every key implicitly mapped to &bottom;. In this way any operation from the embedded type can be applied through a higher-order apply which takes a delta mutator o_i^δ to be applied, the key k, and the map (m,c).

This mutator fetches the value at key k from m, pairs it with the shared causal context c, obtaining a value from the embedded type, and invokes the operation over the pair; from the resulting pair, it extracts the value to create a new mapping for that key, which it pairs with the resulting causal context. Removing a key will recursively remove the dots in the corresponding embedded value, while the clear operation will remove all dots from the store.