FairRide: Near-Optimal, Fair Cache Sharing – Pu et al. 2016
Yesterday we looked at a near-optimal packet scheduling algorithm (LSTF), today it’s the turn of a near-optimal fair cache sharing algorithm. We’re concerned with the scenario where a single cache resource is shared by multiple applications / users. Ideally we’d like three properties to hold:
- Isolation – each user should receive no less cache space than they would if the cache were statically and equally divided between all users. We’re allowed to share the unused cache space of a given user amongst other users, so long as it becomes available to them again if they need it.
- Pareto Efficiency – the operator wants to achieve high utilisation, in an efficient system it is not possible to increase one user’s cache allocation without lowering the allocation of some other user.
- Strategy Proof – we want to protect against users who try to game the system (e.g. by making redundant requests to improve cache retention of their items). I.e., there should be no strategy that a user can follow which serves them better than fair use.
The cache example studied in the paper is caching of files (e.g. in Tachyon, sitting in front of HDFS), and the paper follows the classic ‘2 of 3’ formulation:
The SIP theorem: With file sharing, no cache allocation policy can satisfy all three following properties: strategy-proofness (S), isolation guarantee (I), and Pareto-efficiency (P).
One of the most popular solutions to achieve efficient resource utilization while still providing isolation is max-min fairness. As we’ll see, max-min fairness can be gamed. The authors introduce a new derivative they call FairRide, which by compromising ever so slightly on Pareto-efficiency, is able to provide both isolation and strategy-proofness. Compared to independent (fully isolated caches), FairRide gives a 2.6x cache efficiency improvement, is much more robust in the face of gaming / noisy neighbours in a shared cache environment, and is able to get within 3-13% of the absolute best-case performance while providing these guarantees.
It’s fairly easy to understand why the operator of a cache would want efficiency. Let’s take a moment to consider why isolation and strategy-proofness matter too. Consider a setup hosting multiple sites (A & B) with a shared cache (e.g. Redis or memcached) speeding up access to a back-end database. The authors cite many examples of questions posted on technical forums asking how to achieve isolation in exactly such a scenario. If A and B start off with roughly equal load (and equal cache share) and then A’s load increases significantly while B’s remains constant then the mean latency of B’s requests may increase significantly (2.9x) while A’s latency actually drops as the cache system loads more of A’s results and evicts B’s! Setting up totally separate caching instances per user or application misses the opportunity to share cached files across users (in a production HDFS log for example, 31.4% of files are shared by at least two applications).
One thing that B could do, while being penalised by A in the example above, is to artificially increase its access rate to keep its items in the cache. If A follows suit and plays the same game, everyone loses.
Furthermore, like with prisoner’s dilemma, sites are incentivized to misbehave even if this leads to worse performance for everyone. While in theory users might be incentivized to misbehave, a natural question is whether they are actually doing so in practice. The answer is “yes”, with many real-world examples being reported in the literature…
Max-min fairness is one of the most popular solutions to the problem of achieving efficient resource utilization while still providing isolation. It aims to maximize the minimum allocation across all users by the choosing to evict an item belonging to the user with the largest cache allocation whenever space needs to be made in the cache. If users access disjoint sets of files (or other types of resources being cached) then all is well. But if multiple users can share the same files then max-min fairness is not strategy proof:
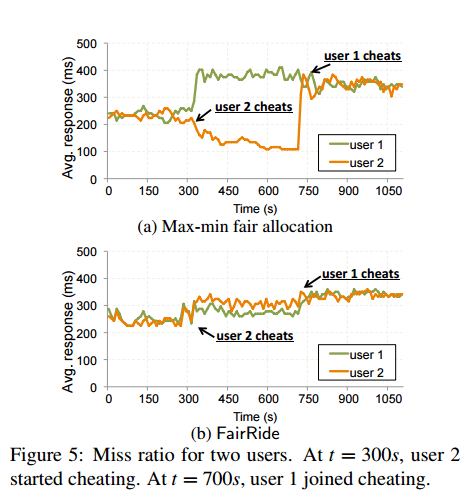
While max-min fairness is strategy-proof when users access different files, this is no longer the case when files are shared. There are two types of cheating that could break strategy-proofness: (i) intuitively, when files are shared a user can ‘free ride’ files that have been already cached by other users, (ii) a thrifty user can choose to cache files that are shared by more users, as such files are more economic due to cost-sharing.
(if a file is accessed by k users, each user will be ‘charged’ with 1/k of the size of that file).
For the two-user case, a user can lose up to 50% of cache/hit rate when all the user’s files are shared and ‘free-ridden’ by the other strategic user…
It is also worth mentioning that for many applications, moderate or even minor cache loss can result in drastic performance drop…. A slight difference in the cache hit ratio, e.g. from 99.7% to 99.4% can mean 2 x I/O average latency drop! This indeed necessitates strategy-proofness in cache policies.
FairRide
FairRide extends max-min fairness with probabilistic blocking.
FairRide provides isolation guarantee and strategy-proofness at the expense of Pareto-efficiency. We use expected delaying to implement the conceptual model of probabilistic blocking.
The only difference between max-min fairness and FairRide is that there is a chance a user might get blocked when accessing data from the cache. The chance of blocking is set at 1/(nj+1), where nj is the number of other users caching the file. “We will prove in section 5 that this is the only and minimal blocking probability setting that will make FairRide strategy-proof.”
In a real system employing blocking, a strategic user can make even more accesses in the hope that one of the accesses is not blocked. So instead, when a user tries to access an in-memory file that is cached by other users, the system delays the data response with a certain wait duration… the wait time should be set as the expected delay a user would experience if that user were probabilistically blocked by the system.
In other words, we have a claim that takes a while to get your head around – your low-latency cache works better if you sprinkle a few sleeps in the code before returning results!!!
FairRide was implemented on top of Tachyon, acting as a cache in front of Hadoop and Spark applications. “We implement delaying by simply sleeping the thread before giving a data buffer to the Tachyon client.”
Tachyon is a distributed system comprised of multiple worker nodes. We enforce allocation policies independently at each node. This means that data is always cached locally at the node when being read, and that when the node is full, we evict from the user who uses up the most memory on that node.
The evaluation showed that this achieved within 3-4% of the theoretical efficiency of global fairness, due to the self-balanced nature of the big data workloads studied on Tachyon. FairRide can prevent user starvation while remaining within 4% of global efficiency, and is 2.6x better than isolated caches in terms of job time reduction, and gives 27% higher utilization compared to max-min fairness.
Figure 5 (reproduced below) shows how FairRide remains strategy-proof in the face of a cheating user:
FairRide was further evaluated by running TPC-H and YCSB benchmarks, and a replay of a production cluster HDFS log from a large internet company. Each workload was run in four different configurations: statically partitioned caches; max-min fairness with no cheating users; FairRide; and max-min fairness with half of all users trying to game the system.
Figure 6 shows how FairRide compares to isolated caches:
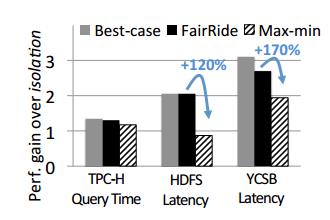
Using max-min fairness with no cheating users improves performance by 1.3-3.1x, but 15-220% of that gain is lost again if users cheat. FairRide gets to within 3-13% of the best case performance gains, but prevents the undesirable performance drop when users do cheat.
For further evaluation details, see the full paper.
Based on the appealing properties and relatively small overhead, we believe that FairRide can be a practical policy for real-world cloud environments.
Coda: On Design Space Trade-offs
Understanding fundamental trade-offs in a design space is always very useful. There are ‘opposing pair’ trade-offs which explore a 2-dimensional space – I mentally picture these as sliders you can set between two extremes. For example, the trade-off between extreme low-latency on the one hand, and extremely high-throughput on the other. Or between security and ease-of-use.
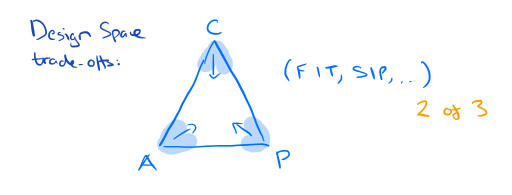
This paper follows the popular X,Y,Z – pick 2 meme. Essentially we’re exploring a three-dimensional space, or you can think of it as a triangle. Take any 2 of the 3, and you don’t have to trade-off between them, but put all three together and you do (interestingly, you can often get very close to the points of the triangle, you just can’t get all the way – this is the difference between the impressive sounding theory and pragmatic system designs). SIP (this paper), FIT, CAP, CAC, and the classic Quality-Function-Schedule all come to mind.
But I don’t know of an example of a higher-order trade-off. I see no theoretical reason why they shouldn’t exist – I just can’t cite one. Consider four dimensions, the formulation A,B,C,D -pick 3. (And it would have to be the case that if you take any 3 of them you don’t have to trade-off between them).
I like to collect trade-offs – if you have examples of 2, 3 (or even 4+) dimensional trade-offs in different areas (and with paper references for extra bonus points, but that’s not necessary) please do post in the comments below.