Universal Packet Scheduling – Mittal et al. 2015

(presented at NSDI ’16)

Is there a universal scheduling algorithm, such that simply by changing its configuration parameters, we can produce any desired schedule? In Universal Packet Scheduling, Mittal et al. show us that in theory there can be no Universal Packet Scheduling (UPS) algorithm which achieves this goal. However, in practice there is an algorithm that comes very close and that can replay the results of a wide range of scheduling algorithms in realistic network settings. That algorithm is Least Slack Time First (LSTF).

…we say a packet scheduling algorithm is universal if it can achieve different desired performance objectives (such as fairness, reducing tail latency, minimizing flow completion times). In particular, we require that the UPS should match the performance of the best known scheduling algorithm for a given performance objective.

If there is no UPS, then we should expect to keep designing new scheduling algorithms as performance objectives evolve. But if there is a UPS, or something close enough to one, then it may well be easier/cheaper to configure an existing implementation of it to achieve the new desired outcome. The absence of a UPS makes a strong argument for switches being equipped with programmable packet schedulers, whereas the existence of a practical UPS “greatly diminishes the need for programmable scheduling hardware.”

When you’re used to thinking of code, data, and configuration as all being somewhat fungible it seems a little odd to see this set out in quite such a black-and-white way. Especially since it turns out that the configuration required for LSTF to achieve different objectives takes the form of different expressions to be evaluated for calculating slack. Nevertheless, I don’t think this detracts from the usefulness of the results, and I can certainly see it would be easier just to change the body of a slack function than create and test a whole new scheduling algorithm regardless.

The Rules

Consider a network with some internal topology. Packets arrive at the network at some known time i(p) (the ingress time of packet p) and leave the network at time o(p) (the egress time of packet p). They follow path(p) through the network. Looking at the schedule produced by some scheduling algorithm (the set of tuples (path(p),i(p),o(p)) for all packets p), it should be possible to configure a UPS so that it would reproduce that schedule given the same i(p) and path(p). Or more precisely, we say that algorithm A’ replays A on a given input if and only if ∀p ∈ P, o'(p) ≤ o(p).

Furthermore, we impose some practical constraints:

1. A UPS must use the same deterministic scheduling logic at every router
2. A UPS can only use information in packet headers and static information about the network topology, link bandwidths, and propagation delays to make its scheduling decisions. It is allowed to modify the header of a packet before forwarding it.
3. When initialising headers at a packet’s ingres node, the only additional information available is path(p) and o(p) from the original schedule.

Condition 3 may sound a little strange (we know the output time at ingress) – but remember that here we are interested in whether the UPS can replay the schedule created by some other algorithm.

However, a different interpretation of o(p) suggests a practical application of replayability (and thus our results): if we assign o(p) as the “desired” output time for every packet p, then the existence of a UPS tells us that if these goals are viable then the UPS will be able to meet them.

The bad news: there is no UPS. The proof is given in an appendix to the paper, and hinges on showing that you can create a schedule in which packet p1 must egress before p2, and another schedule in which packet p2 must egress before p1, and for which the information available at the point the critical scheduling decision must be made is identical in both cases (and therefore the algorithm could not distinguish these cases).

The good news, as we’ll see next, is that LSTF can come pretty close to a UPS in practice…

LSTF Replay

This section of the paper is concerned with discovering the range of different behaviours that LSTF can approximate. So we’re interested in experiments whereby we know the ingress and egress times ( i(p) and o(p) ) and we want to see how close to that ideal LSTF can get.

In LSTF, each packet p carries its slack value in the packet header, which is initialized to slack(p) = (o(p) – i(p) – t_min(p, src(p), dest(p)) ) at the ingress, where src(p) is the ingress of p; dest(p) is the egress of p; t_min(p, α, β) is the time p takes to go from router α to router β in an empty network. The slack value, therefore, indicates the maximum queuing time that the packet could tolerate without violating the replay condition. Each router, then, schedules the packet which has the least remaining slack at the time when its last bit is transmitted. Before forwarding the packet, the router overwrites the slack value in the packet’s header with its remaining slack (i.e. the previous slack time minus how much time it waited in the queue before being transmitted).

It turns out that LSTF can replay all viable schedule with no more than two congestion points per packet, and that there are viable schedules with no more than three congestion points per packet it cannot replay. However, it can get very close to those schedules, that is , LSTF can approximately replay schedules in realistic networks.

The following table summarizes the results of five different experiments (one per row), showing how close this approximation can get in practice.

We consider two metrics. First, we measure the fraction of packets that are overdue (i.e. which do not meet the original schedule’s target). Second, to capture the extent to which packets fail to meet their targets, we measure the fraction of packets that are overdue by more than a threshold value T, where T is one transmission time on the bottleneck link (approx 12µs for 1Gbps).

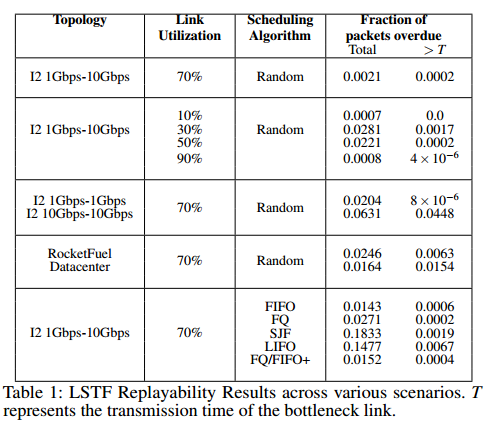
In all but 3 cases, over 97% of packets meet their target output times, and the fraction of packets that did not arrive within T of their target output times is much smaller.

Row 1 in the table is the base case, row 2 shows the impact of link utilization, row 3 explores the impact of varying link bandwidths, row 4 explores the impact of varying network topologies, and row 5 shows how close LSTF can get to a variety of different scheduling algorithms.

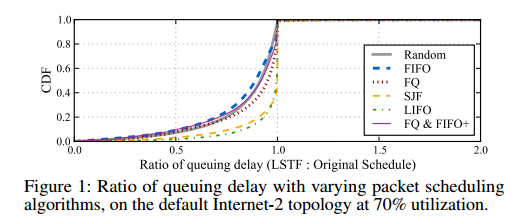
Figure 1 (below) shows the CDF of the ratios of the queueing delay that a packet sees with LSTF to the queuing delay that in sees in the original schedule, for varying packet scheduling algorithms. We were suprised to see that most of the packets actually have a smaller queuing delay in the LSTF replay than in the original schedule. This is because LSTF eliminates “wasted waiting”, in that it never makes packet A wait behind packet B if packet B is going to have significantly more waiting later in its path.

LSTF In Practice

So we know LSTF can achieve lots of different outcomes. But if we have a certain outcome in mind (without being so detailed as to specify the desired output time of every packet!), how do we pragmatically tune LSTF to achieve that outcome? The final part of the paper looks at three common objectives: minimising mean flow completion time, minimising tail packet delays, and achieving fairness.

Mean Flow Completion Time

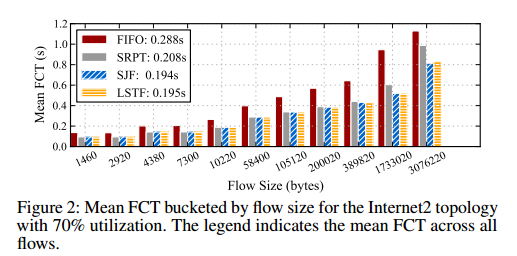
Use slack(p) = flowsize(p)* D, where flowsize(p) is the size of the flow to which the packet p belongs, and D is a value much larger than the delay seen by any packet in the network. This turns out to compare very favourably with Shortest Remaining Processing Time (SRPT) – an algorithm shown to be close to optimal for this problem. Shortest Job First is another algorithm that produces results similar to SRPT for realistic heavy-tailed distributions.

Tail Packet Delay Minimisation

Use slack(p) = C, where C is a constant value eg. 1 sec. This makes LSTF equivalent to the FIFO+ algorithm for minimising tail packet delays in multi-hop networks. LSTF does slighly better than FIFO+ it turns out, as shown below:

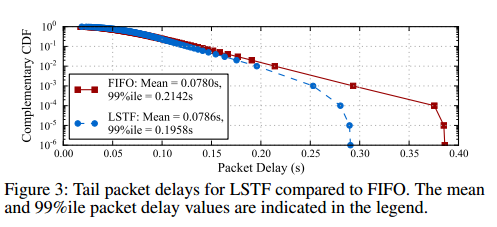
With LSTF, packets that have traversed through more number (sic) of hops, and have therefore spent more slack in the network, get preference over shorter-RTT packets that have traversed through fewer hops. While this might produce a slight increase in the mean packet delay, it reduces the tail.

Fairness

LSTF can achieve asymptotic fairness – eventual convergence to the fair-share rate.

Use

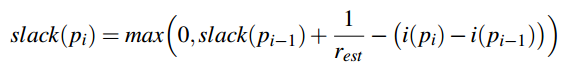
where i(p) is the arrival time of the packet p at the ingress, and r_est is an estimate of the fair-share rate r. This leads to asymptotic fairness for any value of r_est that is less than r, as long as all flows use the same value. r_est can be estimated using knowledge about the network topology and traffic matrices (exercise for the reader!).

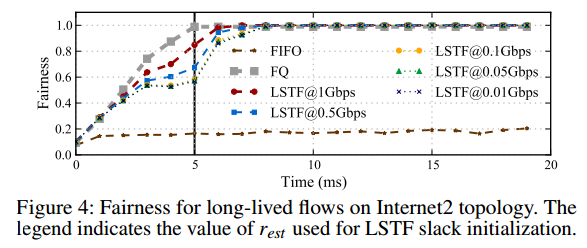
Figure 4 shown the fairness computed using Jain’s Fairness Index, from the throughput each flow receives per millisecond. Since we use the throughput received by each of the 90 flows to compute the fairness index, it reaches 1 with FQ only at 5ms, after all the flows have started. We see that LSTF is able to converge to perfect fairness even when r_est is 100x smaller than r. It converges slightly sooner when r_est is closer to r, though the subsequent differences in the time to convergence decrease with decreasing values of r_est.