Cliffhanger: Scaling Performance Cliffs in Web Memory Caches – Cidon et al. 2016
Cliffhanger continues yesterday’s theme of efficient cache allocation policies when sharing cache resources. The paper focuses on a shared memcached service, where memory is divided between a number of slabs (each slab storing items with sizes in a specific range – e.g. < 128B, 128-256B, and so on). How should we divide the memory in the most efficient way possible, so as to achieve a higher hit rate with the same amount of memory?
These problems are not specific to slab-based memory allocation like Memcached. They also occur in systems like RAMCloud that assign memory contiguously in a log (i.e. in a global LRU queue). Regardless of the memory allocation approach, memory is assigned to requests greedily: when new requests reach the cache server they are allocated memory on a first-come-first-serve basis, without consideration for the request size or the requirements of the requesting application.
There are two very compelling reasons why the results in this paper are of immediate practical significance:
- Cliffhanger increases overall hit rate by 1.2%, and reduces the total number of cache misses by 36.7%. We know that even modest improvements to cache hit rate can impact performance in web applications. “For instance, the hit rate of one of Facebook’s memcached pools is 98.2%. Assuming the average read latency from the cache and MySQL is 200µs and 10ms respectively, increasing the hit rate by just 1% would reduce the [average?] read latency by over 35% (from 376µs at 98.2% to 278µs at 99.2%). The end-to-end speed-up is even greater for user queries, which often wait on hundreds of reads.”
- Cliffhanger can achieve the same hit rate with 45% less memory capacity. When memory is one of the most expensive resources in the datacenter, that’s definitely significant!
Moreover, a micro-benchmark based on measurements at Facebok show a negligible overhead (zero overhead on a cache-hit) in terms of latency and throughput. The data structures used by Cliffhanger add a memory overhead of about 500KB per application.
Cliffhanger is all about global efficiency of the cache – unlike FairRide there is no consideration in the algorithm for ‘fairness’ or isolation between slabs/applications.
Hit Rate Curves & Performance Cliffs
Fundamental to understanding the results in this paper is the concept of a hit rate curve, which shows the probability of finding an item in the cache as the cache size (number of items in the cache) increases.
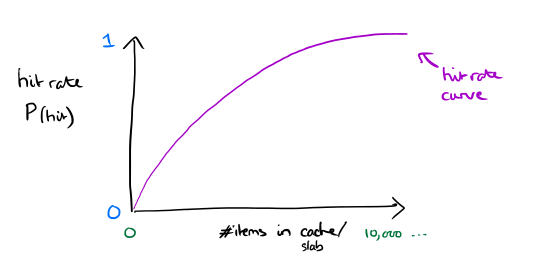
If we know the hit-rate curve for each slab class together with the frequency of requests for each class, a convex solver can tell us the optimal allocations. There are a few challenges with this. Firstly, how do you know what the hit-rate curve looks like in the area beyond the allocated memory size? Stack distances can be used to approximate this.
The stack distance of a requested item is its rank in the cache, counted from the top of the eviction queue. For example, if the requested item is at the top of the eviction queue, its stack distance is equal to 1. If an item has never been requested before, its stack distance would be infinite.
Secondly, estimating the stack distances for each application and running a convex solver is expensive and complex, estimation techniques do not work well with large numbers of items, and of course application workloads change over time.
To address these issues we can use an incremental hill climbing algorithm:
If the gradient of each hit rate curve is known, we can incrementally add memory to the queue with the highest gradient (the one with the steepest hit rate curve), and remove memory from the queue with the lowest gradient. This process can be continued until shifting resources from one curve to the other will not result in overall hit rate improvement.
There still remains one important issue: hill climbing works well as long as the hit rate curves behave concavely and do not experience performance cliffs.
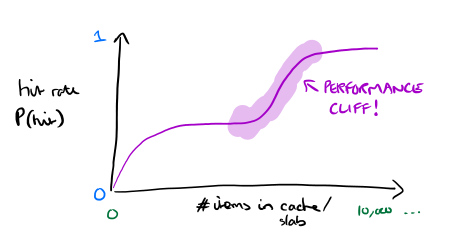
This is true for some, but not for many web applications. Performance cliffs occur frequently in web applications: 6 out of the 20 top applications in our traces have performance cliffs… Performance cliffs are thresholds where the hit rate suddenly changes as data fits in the cache. Cliffs occur, for example, with sequential accesses under LRU. Consider a web application that sequentially scans a 10MB database. With less than 10MB of cache, LRU will always evict items before they hit. However, with 10MB of cache, the array suddenly fills and every access will be a hit. Therefore increasing the cache size from 9MB to 10MB will increase the hit rate from 0% to 100%.
Performance cliffs hurt the hill climbing algorithm because it will underestimate the gradient before a cliff, since it does not have knowledge of the entire hit rate curve.
Cliffhanger is a hill-climbing resource allocation algorithm that runs on each memory cache server and can scale performance cliffs.
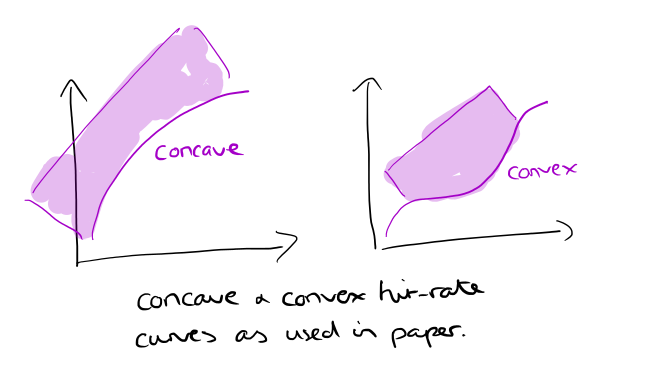
As you read through the paper (and some of the description that follows), you’ll encounter talk of concave and convex hit rate curves / curve regions. These follow the conventions for concave and convex functions, sometimes described as ‘concave & convex downwards’. I personally find this convention counter-intuitive and always have to remind myself which way is which, so here’s a sketch that may help:
How Cliffhanger Climbs Hills
Cliffhanger approximates hit-rate curves using shadow queues in addition to the main eviction queues (LRU, LFU, ..). Each portion of the cache (it could be a slab, or a queue of an entire application) starts out with an allocated cache queue size (e.g. uniform allocation, or there could be some weighting applied). Queue sizes are initialized such that their capacity sums up to the total available memory.
When an item is evicted from a cache queue, the key of the item is added to the corresponding shadow queue. On a cache miss, we look to see if the key is in the shadow queue; if it is we increase the size of the shadow queue by some constant credit amount, and pick another shadow queue at random and decrease its shadow queue size by the same amount. When a shadow queue has reached a certain number of credits, the corresponding cache queue is allocated additional memory at the expense of another cache queue.
[This part of the algorithm is described in both prose and pseudocode, but the prose is ambiguous and the pseudocode doesn’t quite match the prose – the above is my best interpretation of what the authors intended, you can judge for yourself and see if you agree with my interpretation by looking at section 4.1 and Algorithm 1.]
The most important part though, is an understanding of how Cliffhanger scales performance cliffs…
How Cliffhanger Scales Cliffs
Hill-climbing with a shadow queue locally approximates the first derivative of the hit-rate curve. To determine whether a queue is in a convex section of the graph (a cliff), we need to approximate the second derivative as well. And to approximate the second derivative we need two more shadow queues. The cliff climbing shadow queues can be smaller than the hill climbing shadow queue. Furthermore, Cliffhanger actually maintains two copies of all of these queues for each slab/application so that we end up with something that looks like this:
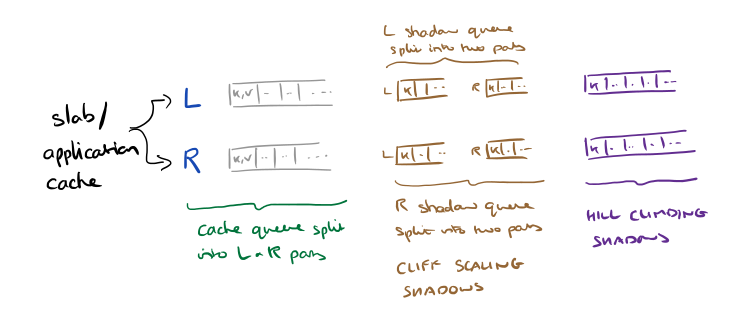
The fundamental idea is to use the ‘left’ queues to manage the portion of the hit rate curve at the bottom of the cliff (to the left of the convex section), and the ‘right’ queues to manage the portion of the hit-rate curve at the top of the cliff (to the right of the convex section). By controlling the fraction of requests directed to the left queue and the fraction of requests directed to the right queue we can achieve the same hit rate as if the performance cliff was not there (simulating the concave hull of the hit rate curve). Of course when we start out, we don’t know where the top and bottom of the cliff is, or even if there is a cliff at all. We incrementally adjust the position of the left and right queues as we go along to figure this out.
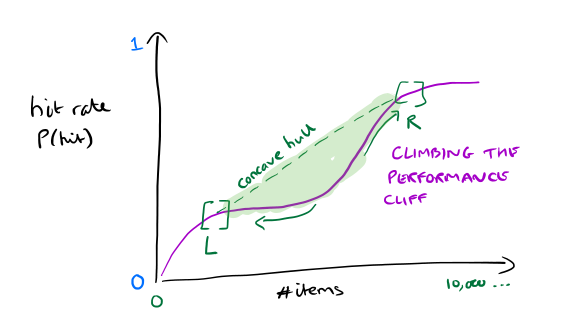
We start out with the cache evenly split between the left and right queues, and the “control valve” set to divide requests evenly between them. “Two evenly split queues behave exactly the same as one longer queue, since the frequency of the requests is halved for each queue, and the average stack distances of each request are also halved.” There are two pointers (the left pointer and the right pointer), and the goal of the algorithm is to move these to the place in the hit rate curve where it starts and stops being convex (the top and bottom of the performance cliff). The two pointers are initialized to the current size of the physical queue.
Suppose the left and right pointers are both currently in a convex region of the hit rate curve. In this case we want to move the left pointer to the left and the right pointer to the right, until they stop being in a convex region…
When a request arrives, we direct it to the left queue with probability Pratio and the right queue with probability (1 – Pratio). If the requested item is not in the cache queue we look in the performance cliff shadow queues. There are four possible places we may find the requested key in a performance cliff shadow queue: the left half of the left queue, the right half of the left queue, the left half of the right queue, and the right half of the right queue.
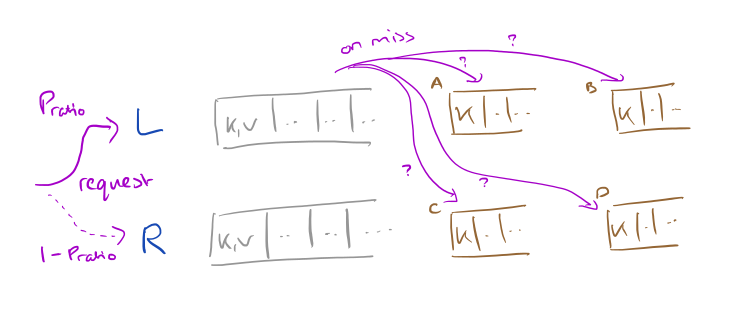
If the key is found in any of these shadow queues, we update the left or right pointer position according to the following table:
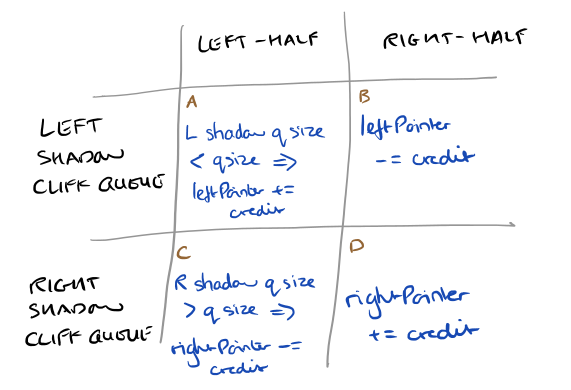
Once the pointers have been updated, the next step is to update the control valve setting (Pratio) to alter the balance of request traffic between the left and right queues.
distanceLeft = queue.size - leftPointer
distanceRight = rightPointer - queue.size
if both distances are greater than zero, then...
requestRatio = distanceRight / (distanceRight + distanceLeft)
else
requestRatio = 0.5
And finally we update the physical (cache) queue sizes:
rightQueue.size = rightPointer * (1 - requestRatio)
leftQueue.size = leftPointer * ratio
The regular hill climbing shadow queue processing also happens as described previously.
Implementation and Evaluation
Cliffhanger is implemented on Memcached in C, using separate hash and queue data structures for the shadow queues.
The implementation only runs the cliff scaling algorithm when the queue is relatively large (over 1000 items), since it needs a large queue with a steep cliff to be accurate. It always runs the hill climbing algorithm, including on short queues. When it runs both of the algorithms in parallel, the 1MB shadow queue used for hill climbing is partitioned into two shadow quee in proportion to the partition sizes. To avoid thrashing, the cliff scaling algorithm resizes the two queues only when there is a miss.
Using Cliffhanger with the trace from 20 applications using a shared Memcachier cache, Cliffhanger on average increases the hit rate by 1.2%, reduces the number of misses by 36.7%, and requires only 55% of the memory to achieve the same hit rate as the default LRU scheme.
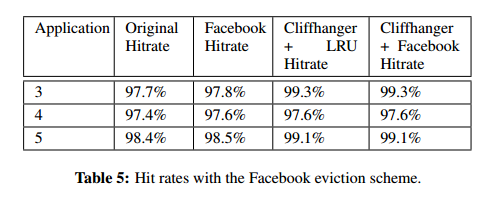
The authors also compared Cliffhanger to the eviction scheme used by Facebook, and to Cliffhanger where the cache queue using the Facebook eviction scheme. In the Facebook scheme, the first time a request hits it is inserted at the middle of the queue, and when it hits a second time it is inserted at the top of the queue. The results are shown below in table 5 for applications 3,4, and 5:
By analyzing a week-long trace from a multi-tenant Memcached cluster, we demonstrated that the standard hit rate of a data center memory cache can be improved significantly by using workload aware cache allocation… The algorithms introduced in this paper can be applied to other cache and storage systems that need to dynamically handle different request sizes and varying workloads without having to estimate global hit rate curves.