Inferring Causal Impact Using Bayesian Structural Time-Series Models – Brodersen et al. (Google) 2015
Today’s paper comes from ‘The Annals of Applied Statistics’ – not one of my usual sources (!), and a good indication that I’m likely to be well out of my depth again for parts of it. Nevertheless, it addresses a really interesting and relevant question for companies of all shapes and sizes: how do I know whether a given marketing activity ‘worked’ or not? Or more precisely, how do I accurately measure the impact that a marketing activity had, so that I can figure out whether or not it had a good ROI and hence guide future actions. This also includes things like assessing the impact of the rollout of a new feature, so you can treat the word marketing fairly broadly in this context.
…we focus on measuring the impact of a discrete marketing event, such as the release of a new product, the introduction of a new feature, or the beginning or end of an advertising campaign, with the aim of measuring the event’s impact on a response metric of interest (e.g., sales).
Following the marketing event, it’s assumed that you can measure the response (sales, clicks, or whatever other metric of interest the marketing event was designed to influence). But what we’d really like to know is the causal impact : the difference between the results that you actually observed, and what would have happened if the marketing event did not take place. The impact of a marketing event is felt over time, so the measured response is a time series variable (e.g. clicks-per-day). Hence we are interested in the difference between the observed time series in the real-world, and the time-series that would have been observed if the intervention had not taken place. As you read through the paper, you’ll find this ‘what would have happened’ time series referred to as the counterfactual.
If we could simply directly measure what would have happened then calculating the difference would be easy. But of course we can’t directly measure it, precisely because it didn’t happen due to our intervention. Therefore we need to build a predictive model of what would have happened (a synthetic control). This has three components:
- The time-series behaviour of the response itself, prior to the intervention.
- The time-series behaviour of other contemporaneous time series that were predictive of the target time-series before the intervention (and are assumed to remain so afterwards, on the basis that they also have not received any intervention). ” Such control series can be based, for example, on the same product in a different region that did not receive the intervention or on a metric that reflects activity in the industry as a whole. In practice, there are often many such series available, and the challenge is to pick the relevant subset to use as contemporaneous controls. This selection is done on the pre-treatment portion of potential controls; but their value for predicting the counterfactual lies in their post-treatment behavior.”
- In a Bayesian framework, the available prior knowledge about the model parameters “as elicited, for example, by previous studies.”
Here’s a picture that might help make all this clearer:
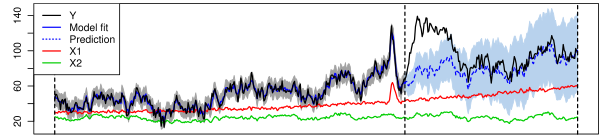
The black line, Y is the metric we’ve been tracking and hoped to influence via the marketing event, so this represents the actual observed behaviour both before and after the intervention. X1 and X2 are two other markets not subject to the intervention that we can use as control series. The solid blue line (in the period before the intervention) shows how well the model has been tracking actuals, the dashed blue line (the period after the intervention) shows what the model predicts would have happened.
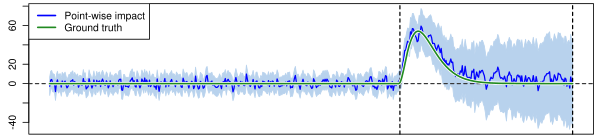
Now we can subtract the prediction of what would have happened (dashed blue line) from what actually happened (Y) to see the true causal impact of the marketing event:
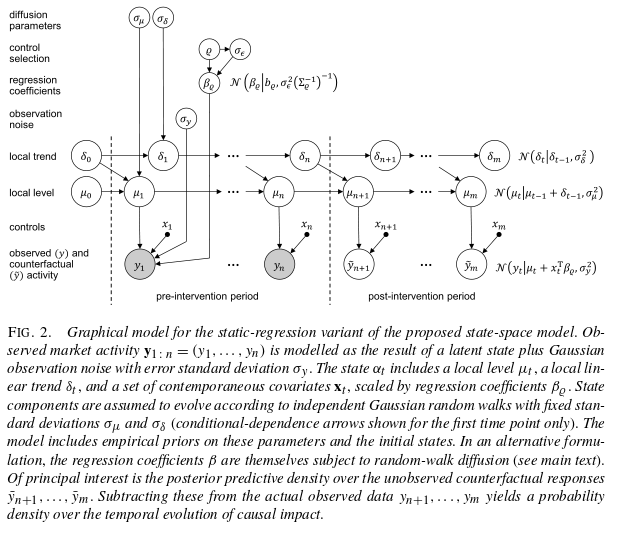
The Bayesian structural time-series models that the authors build for this are based on two equations, one is the observation equation linking observed data to a state vector, and the other is a state equation that describes how the state vector evolves over time. For the state itself they use a local linear trend, which is good for short term predictions, combined with a seasonality model where appropriate. Control time series are included via linear regression, with a choice of either static or dynamic coefficients.
Structural time-series models allow us to examine the time series at hand and flexibly choose appropriate components for trend, seasonality, and either static or dynamic regression for the controls. The presence or absence of seasonality, for example, will usually be obvious by inspection. A more subtle question is whether to choose static or dynamic regression coefficients.
Static coefficients are preferred when the relationship between the controls and the ‘treated unit’ has been stable in the past.
When faced with many potential controls, we prefer letting the model choose an appropriate set. This can be achieved by placing a spike-and-slab prior over coefficients.
Put all the pieces together and you get something that looks a bit like this. For the detailed description, see the full paper!
Of interest of course, is how well this all works…
To illustrate the practical utility of our approach, we analysed an advertising campaign run by one of Google’s advertisers in the United States. In particular, we inferred the campaign’s causal effect on the number of times a user was directed to the advertiser’s website from the Google search results page.
The ad campaign ran for six consecutive weeks and were geo-targeted to a randomised set of 95 out of 190 designated market areas (DMAs).
The outcome variable analysed here was search-related visits to the advertiser’s website, consisting of organic clicks (i.e., clicks on a search result) and paid clicks (i.e., clicks on an ad next to the search results, for which the advertiser was charged). Since paid clicks were zero before the campaign, one might wonder why we could not simply count the number of paid clicks after the campaign had started. The reason is that paid clicks tend to cannibalise some organic clicks. Since we were interested in the net effect, we worked with the total number of clicks.
Prior to the intervention the model provided an excellent fit to the observed data, and you can then post intervention you can see the observed results diverging from the counterfactual (what-if-we-hadn’t-intervened) trend line.
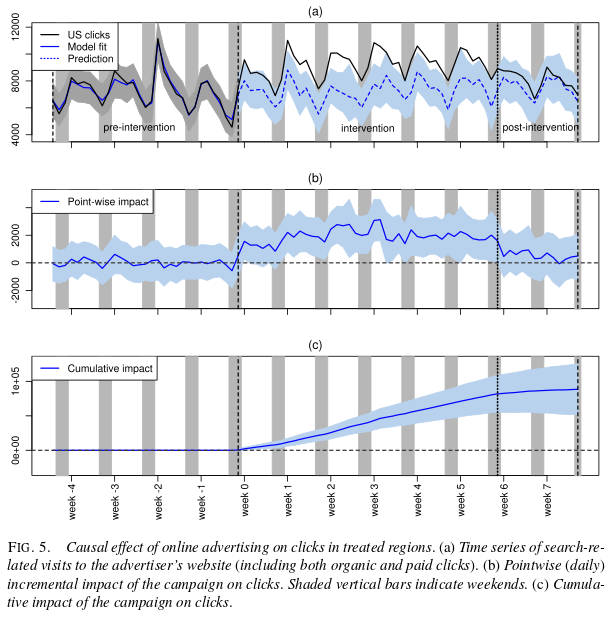
The overall effect estimated by the model was an additional 88,400 clicks. The original experiment was actually conducted with a conventional control, which enabled the team to assess how well their model stacked up against it. The conventional control gave an estimated uplift of 84,700 clicks. (Statisticians will probably hate me here for eliding all the details about confidence intervals etc. when reporting these numbers ;)).
An important characteristic of counterfactual-forecasting approaches is that they do not require a setting in which a set of controls, selected at random, was exempt from the campaign. We therefore repeated the preceding analysis in the following way: we discarded the data from all control regions and, instead, used searches for keywords related to the advertiser’s industry, grouped into a handful of verticals, as covariates. In the absence of a dedicated set of control regions, such industry related time series can be very powerful controls, as they capture not only seasonal variations but also market-specific trends and events (though not necessarily advertiser-specific trends). A major strength of the controls chosen here is that time series on web searches are publicly available through Google Trends (http://www.google.com/trends/). This makes the approach applicable to virtually any kind of intervention.
And this ‘no cheating’ version of the model found an estimated cumulative uplift of 85,900 clicks, replicating almost perfectly the original analysis.
The authors conclude:
Overall, we expect inferences on the causal impact of designed market interventions to play an increasingly prominent role in providing quantitative accounts of return on investment [Danaher and Rust (1996), Leeflang et al. (2009), Seggie,Cavusgil and Phelan (2007), Stewart (2009)]. This is because marketing resources, specifically, can only be allocated to whichever campaign elements jointly provide the greatest return on ad spend (ROAS) if we understand the causal effects of spend on sales, product adoption or user engagement. At the same time, our approach could be used for many other applications involving causal inference. Examples include problems found in economics, epidemiology, biology or the political and social sciences. With the release of the CausalImpact R package we hope to provide a simple framework serving all of these areas. Structural time series models are being used in an increasing number of applications at Google, and we anticipate that they will prove equally useful in many analysis efforts elsewhere.