‘Cause I’m Strong Enough: Reasoning About Consistency Choices in Distributed Systems – Gotsman et al. 2016

With apologies for the longer write-up today, I’ve tried to stick right to the heart of the matter, but even that takes quite some explanation…

We’ve looked at the theme of coordination avoidance before – instead of uniformly applying a stronger form of consistency to all operations, we can consider applying it only in those cases where its absence would lead to violation of application integrity constraints. This leads to hybrid consistency models where different levels of consistency are applied to different operations. Given a set of application invariants, how do you know how much consistency is enough? And what form should the extra coordination take to achieve it? In today’s paper, Gotsman et al. introduce “the first proof rule for establishing that a particular choice of consistency guarantees for various operations on a replicated database is enough to ensure the preservation of a given data integrity invariant.”

The Rule also has the important property of modularity: you can reason about the behaviour of every operation individually, and the results compose.

We have also developed a prototype tool that automates our proof rule by reducing checking its obligations to SMT queries (§6). Using the tool, we have verified several example applications that require strengthening consistency in nontrivial ways. These include an extension of the above banking application, an online auction service and a course registration system. In particular, we were able to handle applications using replicated data types (aka CRDTs), which encapsulate policies for automatically merging the effects of operations performed without synchronisation at different replicas. The fact that we can reduce checking the correctness properties of complex computations in our examples to querying off-the-shelf SMT tools demonstrates the simplicity of reasoning required by our approach.

So what is this all-powerful rule? Here you go:

Perhaps that warrants a little further explanation ;). I’ll use the rest of this post to try and build us back up to a point where you can understand the above and its implications.

Aside: the POPL papers we’re looking at this week are all quite dense with proofs and formalisms. These take longer (for me at least) to work through. Don’t be put off by all the symbols though – two things I find helpful are (a) making a little decoding table of symbol -> meaning on a scrap of paper as you read along, and (b) imaging a translation to e.g. data type and function definitions in your favourite programming language. This latter exercise quite often leads to ‘oh, they just mean that‘ moments for me…

A Model for Causal Consistency and How to Strengthen It

Causal consistency can be implemented without any synchronisation. All replicas see causally-dependent events (as defined by some happens-before partial ordering) in the order in which they happened. Replicas may see causally independent events in different orders.

Such anomalies related to the ordering of actions are often acceptable for applications. What is not acceptable is to violate crucial well-formedness properties of application data, called integrity invariants. Consistency models that do not require any synchronisation are often too weak to ensure these.

Take the classic example of an integrity constraint saying that a balance may not go below zero (yes, it’s very over-simplified). Giving a starting balance of 100, and two independent withdrawals of 75 at two different replicas, this constraint will be violated.

The paper introduces a general model for consistency, and although it is not implemented as described in any known datastore, it is sufficiently general to model the behaviours of many known implementations. Let us begin…

• Consider a set of replicas r₁, r₂, r₃, … , r_n each maintaining a full copy of the database state.
• Let client operations initially execute in linear fashion at a single replica, known as the origin replica.
• Operations deterministically update the state at the origin replica and return a value to the client. The effect (updates made to state) of the operation is then sent to all other replicas.
• Replicas are guaranteed to receive this update message at most once, and upon receipt they apply the effect to their state.

We can think of the behaviour of operations as being defined by some function F:

F :: Operation -> State -> (Val, (State -> State))

That is, given an operation, when it is applied to some state we get back a return Val for the client, and an effect function (State -> State) that can be applied at other replicas. We write F_o to represent the partial application of F to the operation o. This of course gives us a function that takes a State and returns a (Value, Effect) pair. States are represented by the symbol σ so F_o(σ) is the operation o applied to the state σ We’re going to want to talk about return value and effects a lot, so let’s define a convenient shorthand for those too:

• Let F_o^val(σ) = fst(F_o(σ)). (i.e., the value component of the pair)
• And let F_o^eff(σ) = snd(F_o(σ)) (i.e., the effect component of the pair)

We could specify an operation for applying interest in the account example as follows:

F_interest(σ) = (⊥,(λσ’.σ’ + 0.5 * σ))

Note that this function is rather carefully designed to calculate the interest using the balance at the origin replica, and then just add the result at all other replicas. If instead we did the interest calculation at each replica, it would be possible for balances to diverge…

This is undesirable for database users: we would like the implementation to be convergent, i.e., such that two replicas that see the same set of operations are in the same state. In particular, if users stop performing updates to the database, then once all outstanding messages are delivered, all replicas should reach the same state. To ensure convergence, for now we require that the effects of all operations commute… The requirement of commutativity is not very taxing: … programmers can exploit ready-made replicated data types (aka CRDTs). These encapsulate commutative implementations of policies for merging concurrent updates to the database.

(Ok, I see where you’re coming from, but I’m not convinced it’s quite that easy: we still need it to be the case there are suitable CRDTs for the state we wish to represent, and we still need to reason carefully about their composition…).

So much for the baseline. What about invariants that can’t be preserved in this model – how would we strengthen consistency to accommodate them?

Consider our invariant that a balance always stays above 0: if we check there are sufficient funds as part of a withdraw operation we can preserve the invariant at a single replica, but we can’t prevent operations processed asynchronously at different replicas from leading to a converged state that violates it.

The problem in this example arises because two particular operations update the database concurrently, without being aware of each other. To address this, our consistency model allows the programmer to strengthen causal consistency by specifying explicitly which operations may not be executed in this way.

The ‘one weird trick’ 😉 that makes all this work is the introduction of a token system to the model. A A token system comprises a set of tokens, Token, and a symmetric conflict relation ⋈ ⊆ Token x Token. We also set that a set of tokens T₁ conflicts with a set of tokens T₂ if any token in T₁ conflicts with at least one token in T₂ (written T₁ ⋈ T₂).

Now we have to extend our earlier definition of F so that an operation also returns the set of Tokens it acquired:

F :: Operation -> State -> (Val, (State x State), ℘Token)

And we’ll denote the set of tokens returned from applying an operation o in state σ as F_o^tok(σ).

The consistency model is defined such that operations which acquire tokens that conflict with each other according to the conflict relation ⋈ must be causally dependent (i.e., there must be a happens-before relationship between them that provides an ordering). Ensuring this in an implementation requires replicas to synchronize (see e.g. Bolt-on Causal Consistency and Putting the Consistency back into Eventual Consistency).

To protect the withdraw operation, it is enough to ensure that withdraw acquires a token, τ conflicting with itself. (Which in this case, will act a bit like a mutual exclusion lock). Given the presence of a token system, we can weaken the requirement that operations commute to only require commutativity for operations that do not acquire tokens.

If we don’t use any tokens at all, then we get the baseline causal consistency. If every operation acquires a token τ that is in conflict with itself, then we get sequential consistency. In between these two extremes all sorts of interesting combinations are possible. For example, the red-blue hybrid consistency model guarantees sequential consistency to red operations, and only causal consistency to blue operations. To express this we’ll have red operations acquire our self-conflicting τ token again, and blue operations don’t acquire any tokens.

The Rule, Revisited

Given a token system (a set of tokens and a conflict relation), and a set of operations F, how can we show that an invariant I over the set of allowable database states will always hold? To do this we need to introduce a Guarantee relation, G(τ), that describes all the possible state changes that an operation holding token τ can cause. ” Crucially, this includes not only the changes that the operation can cause on the state of its origin replica, but also any change that its effect causes at any other replica it is propagated to.” The special G₀ relation specifies the possible state changes from an operation that does not hold any tokens. Using the guarantee relation we can reason about operations (strictly, sets of operations sharing a token?) independently.

It’s time to revisit The Rule. The specification expresses invariants in a way you may not be so familiar with if you’re used to seeing invariants as predicates. Instead an invariant I is expressed as a subset of all possible states – the invariant holds if the state of the system always stays within this subset. Same thing ultimately.

∃ G₀ ∈℘(State x State), G ∈ Token -> ℘(State x State ), such that…

( To show that an invariant will always hold we must be able to specify a G₀ and a G(τ) relation such that…)

• S1: σ_init ∈ I

( the initial state preserves the invariant. )

• S2: G₀(I) ⊆ I ∧ ∀(τ). G(τ)(I) ⊆ I

(If you are in a state in which invariant I holds, and you execute an operation that does not acquire any tokens, you are guaranteed to end up in a state in which the invariant I also holds. AND, for every token in the token system, if you execute an operation that requires that token when in a state in which the invariant holds, then you are guaranteed to end up in a state in which the invariant holds.)

• S3: ∀o,σ,σ’. (σ ∈ I ∧ (σ,σ’) ∈ (G₀ ∪ G((F_o^tok(σ))^⊥))*) => …

(Take any operation o, and the states σ, σ’. Then if the invariant I holds in state σ, and σ’ is a state reachable from σ under G₀, or a state reachable from σ under G(τ) where τ is any token that does not conflict with those acquired by the operation o, this implies….)

… => (σ’, F_o^eff(σ)(σ’)) ∈ G₀ ∪ G₀^tok(σ))

(the implication: the state reached by applying the effect function from operation o to σ’, preserves the guarantees in the case of no tokens and in the case of the tokens acquired by operation o. )

Or, as the authors put it:

Coondition S3 considers an arbitrary state σ of o’s origin replica r, assumed to satisfy the invariant I. The condition then considers any state σ’ of another replica r’ to which the effect of o is propagated. The conclusion of S3 requires us to prove that applying the effect F_o^eff(σ) of the operation o to the state &sigma’; satisfies the union of G₀ and the guarantees associated with the tokens F₀^tok(σ) that the operation o acquires.

Examples and Applications

Let’s try applying The Rule to show that the invariant of our little banking example is maintained.

Here’s the specification of the operations:

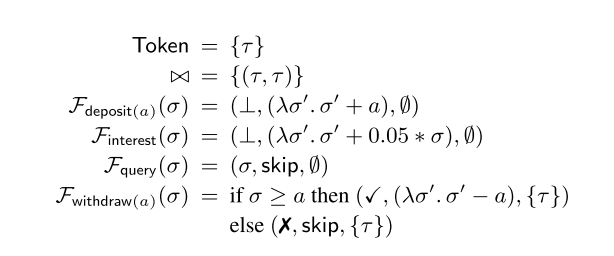
And we want to show the invariant I = { σ | σ ≥ 0} (the entire state boils down to a single number in this example).

S1: is rather easy to show, just pick an initial balance, e.g. 0, that satisfies I. σ_init = 0, 0 ≥ 0.

What are the guarantees? Any operation not requiring a token must leave the balance at least as high as it was before:

G₀ = {(σ,σ’) | 0 ≤ σ ≤ σ’}

And any operation (just withdrawal here) acquiring the single token τ in the token system must leave the balance greater than zero (we’re also not allowed to withdraw negative amounts):

G(τ) = {(σ,σ’) | 0 ≤ σ’ ≤ σ}

Given these guarantees, if we can show S2 and S3 hold, then we know that the invariant will always hold. Condition S2 is easy to show – under G₀ the balance can only increase and hence will always be positive, and under G(τ) the balance can never become less than zero.

How do we show S3? The most interesting case is the withdrawal operation withdraw(a) where we want to withdraw some amount a. There is only one token in the whole system, τ so there are no operations that acquire a token other than τ. This means the premise of S3 boils down to states reachable from the initial state under G₀. Therefore we know that 0 ≤ σ ≤ sigma;’. If σ < a (there isn't enough money) then F^eff(σ) leaves the balance unchanged. Thus (σ’, σ’) ∈ G₀ and the conclusion holds. If on the other hand we have enough money at the origin (σ ≥ a) then F^eff(σ) is just σ’ – a. We’ve already shown that σ ≤ σ’, and σ ≥ a, therefore σ’ ≥ a and hence (σ’,σ’-a) ∈ G^eff(τ) and the conclusion also holds.

Operationally, in this case our proof rule establishes that, if there was enough money in the account at the replica where the withdrawal was made, then there will be enough money at any replica the withdrawal is delivered to. This completes the proof of our example.

What would we do in the more realistic example of an application managing multiple accounts? Simply associate every account c with its own token τ_c, and have each τ_c conflict only with itself.

Thus, withdrawals from the same account would have to synchronise, while withdrawals from different accounts could proceed without synchronisation.

There are many more examples in the paper itself, which space prevents me from describing here.