Petuum: A New Platform for Distributed Machine Learning on Big Data – Xing et al. 2015
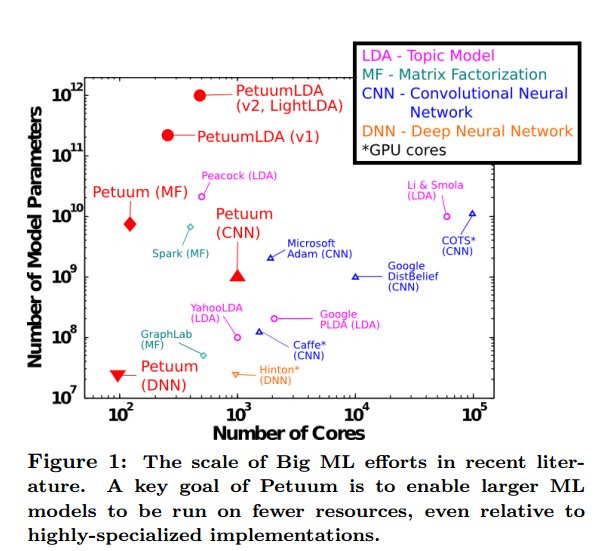
How do you perform machine learning with big models (big here could be 100s of billions of parameters!) over big data sets (terabytes or petabytes)? Take for example state of the art image recognition systems that have embraced large-scale deep learning models with billions of parameters… and then try to apply them to terabytes of image data. Topic models with up to a million parameters cover long-tail semantic word sets for substantially improved advertising; very high-rank matrix factorisation improves prediction in collaborative filtering…
The following matrix gives a good indication of the scale of problems Petuum is designed to address:
As we saw previously in ‘Asynchronous Complex Analytics in a Distributed Dataflow Architecture‘ state of the art machine learning algorithms tend to be designed for single machines, and are hard to implement efficiently on distributed data processing frameworks as-is (e.g. Hadoop MR, Spark, GraphLab, and Pregel). The rigidity of the underlying Bulk Synchronous Parallel computation model is too restrictive. Gonzalez et al. propose introducing ‘asynchronous sideways information passing’ (ASIP) channels on top of the BSP model. The Petuum team relax the synchronization requirements using a Slack Synchronous Parallel (SSP) model. This is possible because of the inherent characteristics of machine learning algorithms. Most (if not all) machine learning algorithms are ‘iterative-convergent’ – they execute an update function over model state repeatedly until some stopping criteria is reached.
It is noteworthy that iterative-convergent computing tasks are vastly different from conventional programmatic computing tasks (such as database queries and keyword extraction), which reach correct solutions only if every deterministic operation is correctly executed, and strong consistency is guaranteed on the intermediate program state — thus, operational objectives such as fault tolerance and strong consistency are absolutely necessary. However, an ML program’s true goal is fast, efficient convergence to an optimal solution, and we argue that fine-grained fault tolerance and strong consistency are but one vehicle to achieve this goal, and might not even be the most efficient one.
Petuum is a distributed machine learning platform built around the characteristics of machine learning algorithms – iterative-convergent, error tolerance, dynamic structure, and non-uniform convergence.
These properties present unique opportunities for an integrative system design, built on bounded-latency network synchronization and dynamic load-balancing scheduling, which is efficient, programmable, and enjoys provable correctness guarantees. We demonstrate how such a design in light of ML-first principles leads to significant performance improvements versus well-known implementations of several ML programs, allowing them to run in much less time and at considerably larger model sizes, on modestly-sized computer clusters.
Background – limitations of existing distributed frameworks for ML use cases
The simplicity of the MapReduce abstraction makes it difficult to exploitML properties such as error tolerance (at least, not without considerable engineering effort to bypass MapReduce limitations), and its performance on many ML programs has been surpassed by alternatives. One such alternative is Spark, which generalizes MapReduce and scales well on data while offering an accessible programming interface; yet, Spark does not offer fine-grained scheduling of computation and communication, which has been shown to be hugely advantageous, if not outright necessary, for fast and correct execution of advanced ML algorithms.
(The ASIP channels mentioned earlier provide fine-grained communication on top of Spark).
Graph-centric platforms such as GraphLab and Pregel efficiently partition graph-based models with built-in scheduling and consistency mechanisms; but ML programs such as topic modeling and regression either do not admit obvious graph representations, or a graph representation may not be the most efficient choice; moreover, due to limited theoretical work, it is unclear whether asynchronous graph-based consistency models and scheduling will always yield correct execution of such ML programs.
Exploiting ML algorithm properties
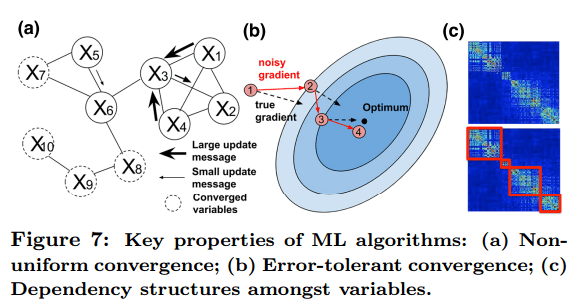
Error Tolerance
Machine learning algorithms are often tolerant of limited errors in intermediate calculations. Suppose you’re headed downhill towards a (hopefully global) minimum – whether you take a direct straight line from your current position to the minimum, or you tack across the hillside a little on the way down, gravity will ensure you end up in the same place in the end. When machine learning in parallel, the extra coordination required to take the most direct path adds a lot of overhead – so we can be more efficient overall if we allow looser coordination and just keep on course correcting as need be.
Petuum synchronizes the parameter states with a bounded staleness guarantee, which achieves provably correct outcomes due to the error-tolerant nature of ML, but at a much cheaper communication cost than conventional per-iteration bulk synchronization.
Petuum’s bounded staleness guarantee is provided by using Stale Synchcronous Parallel (SSP) consistency in-place of BSP.
The SSP consistency model guarantees that if a worker reads from the parameter server at iteration c, it is guaranteed to receive all updates from all workers computed at and before iteration c – s – 1, where s is the staleness threshold. If this is impossible because some straggling worker is more than s iterations behind, the reader will stop until the straggler catches up and sends its updates. For stochastic gradient descent algorithms (such as in the DML program), SSP has very attractive theoretical properties…
Dynamic Structural Dependency
During execution of a machine learning algorithm the correlation strengths between different model parameters alters. This information can be used by a scheduler to minimize parallelization error and synchronization costs. Petuum enables model parameters to be partitioned across multiple machines, not just data. The distribution of model parameters can change over time to match the evolving dynamic structural dependencies.
Non-uniform convergence
The number of steps needed for a parameter to converge can be highly skewed across parameters. Petuum therefore enables a scheduler to prioritize computation towards non-converged model parameters and thus achieve faster overall convergence.
Compare and Contrast…
…central to Spark is the principle of perfect fault tolerance and recovery, supported by a persistent memory architecture (Resilient Distributed Datasets); whereas central to GraphLab is the principle of local and global consistency, supported by a vertex programming model (the Gather-Apply-Scatter abstraction). While these design principles reflect important aspects of correct ML algorithm execution — e.g., atomic recoverability of each computing step (Spark), or consistency satisfaction for all subsets of model variables (GraphLab) — some other important aspects, such as the three statistical properties discussed above, or perhaps ones that could be more fundamental and general, and which could open more room for efficient system designs, remain unexplored.
Data-parallelism and Model-parallelism
The Petuum computation model is design to support both data parallelism and model parallelism. Data parallelism is of course very familiar to us.
In data-parallel machine learning, we partition the data and distribute it across multiple workers. Workers apply the update function to each of these data subsets in parallel. Algorithms suited to a data parallel implementation must have a way of aggregating the results from each data subset…
For example, in distance metric learning problem which is optimized with stochastic gradient descent (SGD), the data pairs are partitioned over different workers, and the intermediate results (subgradients) are computed on each partition and are summed before being applied to update the model parameters…
In addition to ‘additive updates,’ we also require the property that each worker contributes equally to the progress of the algorithm no matter which data subset it uses:
Importantly, this additive updates property allows the updates ∆() to be aggregated at each local worker before transmission over the network, which is crucial because CPUs can produce updates ∆() much faster than they can be (individually) transmitted over the network. Additive updates are the foundation for a host of techniques to speed up data-parallel execution, such as minibatch, asynchronous and bounded-asynchronous execution, and parameter servers. Key to the validity of additivity of updates from different workers is the notion of independent and identically distributed (iid) data, which is assumed for many ML programs, and implies that each parallel worker contributes “equally” (in a statistical sense) to the ML algorithm’s progress via ∆(), no matter which data subset Dp it uses.
In model-parallelism, the model itself is partitioned and distributed across workers (recall that in big models, we may even be approaching a trillion parameters – which is pretty mind-blowing when you pause to think about it…). A scheduling function is used to restrict the set of parameters that a given worker operates on.
Unlike data-parallelism which enjoys iid data properties, the model parameters Aj are not, in general, independent of each other, and it has been established that model-parallel algorithms can only be effective if the parallel updates are restricted to independent (or weakly-correlated) parameters [18, 5, 25, 20]. Hence, our definition of model-parallelism includes a global scheduling mechanism that can select carefully-chosen parameters for parallel updating. The scheduling function S() opens up a large design space, such as fixed, randomized, or even dynamically-changing scheduling on the whole space, or a subset of, the model parameters. S() not only can provide safety and correctness (e.g., by selecting independent parameters and thus minimize parallelization error), but can offer substantial speed-up (e.g., by prioritizing computation onto non-converged parameters). In the Lasso example, Petuum uses S() to select coefficients that are weakly correlated (thus preventing divergence), while at the same time prioritizing coefficients far
from zero (which are more likely to be non-converged).
The Petuum System
A Petuum system comprises a set of workers, a scheduler, and a parameter server. The scheduler enables model-parallelism through a user-defined schedule function that outputs a set of parameters for each worker. A dependency-aware scheduler can support re-ordering of variable/parameter updates to accelerate model-parallel ML algorithms such as Lasso regression. “This type of schedule analyzes the dependency structure over model parameters A, in order to determine their best parallel execution order.” A prioritizing scheduler can exploit uneven convergence in ML by prioritizing subsets of variables according to algorithm-specific criteria, such as the magnitude of each parameter, or boundary conditions such as KKT.
Because scheduling functions schedule() may be compute-intensive, Petuum uses pipelining to overlap scheduling schedule() computations with worker execution, so that workers are always doing useful computation. The scheduler is also responsible for central aggregation via the pull() function (corresponding to F()), if it is needed.
A worker receives the set of parameters to be updated from the scheduler, and executes the user-defined push() function to update the model on its data. As push updates model parameters, these are automatically synchronised with the parameter server.
Petuum intentionally does not specify a data abstraction, so that any data storage system may be used — workers may read from data loaded into memory, or from disk, or over a distributed file system or database such as HDFS.
The parameter server(s) provides global shared access to model parameters via a distributed shared-memory API similar to a key-value store.
To take advantage of ML-algorithmic principles, the PS implements Stale Synchronous Parallel (SSP) consistency, which reduces network synchronization costs, while maintaining bounded-staleness convergence guarantees implied by SSP.
Fault-tolerance in Petuum is currently handled via checkpoint and restart.
Example algorithms and Evaluation
The paper contains examples of several algorithms expressed using the Petuum model: data-parallel distance-metric learning; a model-parallel Lasso algorithm; a simultaneous data-and-model parallel approach to LDA; model-parallel matrix factorization; and data-parallel deep learning.
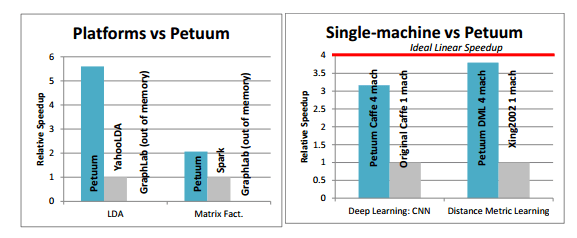
Petuum’s ML-centric system design supports a variety of ML programs, and improves their performance on Big Data in the following senses: (1) Petuum implementations of DML and Lasso achieve significantly faster convergence rate than baselines (i.e., DML implemented on single machine, and Shotgun); (2) Petuum ML implementations can run faster than other platforms (e.g. Spark, GraphLab), because Petuum can exploit model dependencies, uneven convergence and error tolerance; (3) Petuum ML implementations can reach larger model sizes than other platforms, because Petuum stores ML program variables in a lightweight fashion (on the parameter server and scheduler); (4) for ML programs without distributed implementations, we can implement them on Petuum and show good scaling with an increasing number of machines. We emphasize that Petuum is, for the moment, primarily about allowing ML practitioners to implement and experiment with new data/model-parallel ML algorithms on small-to-medium clusters.
(Small-to-medium here means 10-100 servers).
There are many more details in the paper of course. Figure 9 should give you a quick indication of how well Petuum performs relative to other popular implementations, and also of Petuum’s CoST.
6 thoughts on “Petuum: A New Platform for Distributed Machine Learning on Big Data”
Comments are closed.