Distributed consensus revised – Part III

~ Adrian Colyer

Distributed consensus revised (part III) Howard, PhD thesis

With all the ground work laid, the second half of the thesis progressively generalises the Paxos algorithm: weakening the quorum intersection requirements; reusing intersections to allow decisions to be reached with fewer participants; weakening the value selection rules; and sharing phases to take best advantage of the generalisation.

The result of this thesis is a family of approaches to achieving distributed consensus, which generalise over the most popular existing algorithms such as Paxos and Fast Paxos.

Quorum intersection revised

Classic Paxos requires all quorums to intersect, but this turns out to be a stronger condition than is actually required to guarantee safety and progress.

Our first finding is that it is only necessary for phase one quorums and phase two quorums to intersect. There is no need to require that phase one quorums intersect with each other nor that phase two quorums intersect with each other.

This finding (‘revision A’) was also discussed in the Flexible Paxos paper that we’ve covered in a previous edition of The Morning Paper. So long as one quorum member is around to carry the learnings from phase one into phase two, we’re good (the thesis itself provides the proof for this of course).

It turns out we can go even further than this, and differentiate quorums by their epoch as well as by phase. With epoch-specific quorums, the requirement can be further refined (‘revision B’) to require only that a phase two quorum for a given epoch intersects with the phase one quorums of all smaller epochs.

A key implication of this result is that for the minimum epoch there is no phase one quorum intersection requirement. The practical application of this is that a proposer with epoch e_{min} may skip phase one and proceed directly to proposing their own value in phase two.

Furthermore, the phase two bypass optimisation can now kick in whenever we have a phase two quorum of acceptors rather than requiring a full majority.

We can also play with performance and availability trade-offs. For example, in “All aboard Paxos” we colocate proposers and acceptors so that phase one can be completed locally, and we’re still guaranteed a quorum intersection so long as a quorum for phase two requires all acceptors. Or we can flip that on its head (“Singleton Paxos”) and require all acceptors to form a quorum in phase one, allowing any single acceptor to from a quorum in phase two.

Promises revised

Classic Paxos requires a proposer to wait for sufficient promises before proceeding. The one exception we’ve seen to that so far was the phase two bypass when a majority of acceptors return the same proposal during phase one.

If a proposer with epoch e receives a proposal in a promise response promise(e, f, v), then it has learned that if a decision was reached in epoch f, then the value chosen was v. This allows us to further weaken the quorum intersection requirement (‘revision C’): the proposer no longer needs no intersect with the phase two quorums for epochs up to and including f, but must continue to intersect with any phase two quorums for epochs greater than f (up to e of course, its current epoch).

One practical application of this is that a proposer receiving a promise message for the immediate predecessor of the current epoch can proceed directly to phase two.

Value selection revised

In Classic Paxos, the value proposed in phase two is the value associated with the highest epoch received from the acceptors.

In this section… we generalise over the classic value selection rules, by exploiting the additional insight that a proposer gains from each promise it receives. We refer to our revised technique as Quorum-based value selection and it can give proposers more flexibility when choosing a value to propose.

Ignoring epochs for the moment, the first idea is to consider each possible quorum, and whether or not that quorum could have reached a decision. If no quorum could have reached a decision then we’re free to propose our own value. For example, let the set of acceptors be \{a_1, a_2, a_3, a_4, a_5\} and the possible quorum sets be \{a_1, a_2, a_3\} and \{a_4, a_5\}. A proposer in epoch 5 receives the following promises in order:

  • promise(5, 3, A) from a_1
  • promise(5, nil, nil) from a_ 2
  • promise(5, 2, B) from a_4

With Classic Paxos the proposer would have to propose A (the value associated with the highest epoch). But here we know that A cannot have been decided because the nil response from a_2 makes that impossible. Since we have a returned proposal (3, _), we also know that the proposal (2, B) from a_4 cannot have been successful.

If we’re using revisions B and C then we can extend this logic to also track quorum decisions by epoch.

Epochs revised

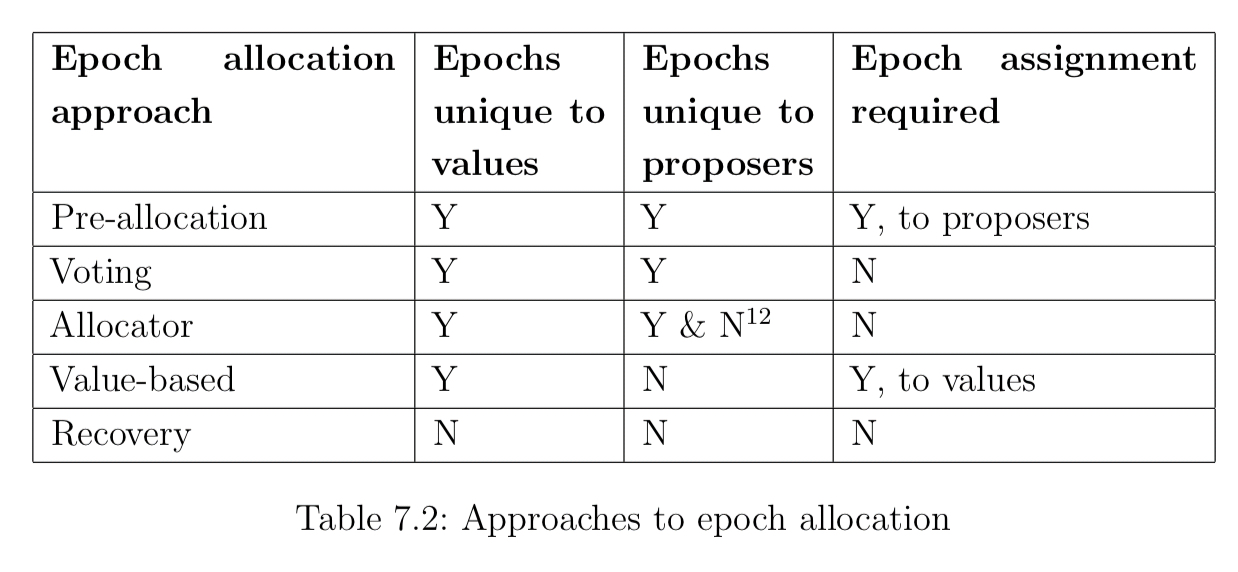
Chapter 7 in the thesis looks at three different strategies to remove the need to pre-allocate or vote for unique epochs among proposers.

One such strategy is to use a singleton allocator, and have every proposer ask the allocator for an epoch each time. The allocator could implement e.g. a simple counter. This has the disadvantage of course of making the allocator a single point of failure.

Another strategy in the case were we know the finite set of possible values that can be decided up front is to pre-allocate epochs to those values. Now proposers proposing a value v use the epochs associated with the value they wish to propose.

Section 7.3 gives a more generally applicable technique, called epochs by recovery. The central idea, as the name suggests, is that instead of trying to ensure up front that the epochs used by proposers will all be unique, we instead allow proposers to use any epoch and add a recovery mechanism to undo the damage if it turns out that multiple values end up being proposed for the same epoch.

So in total we’ve now seen 5 different epoch allocation strategies, as summarised in the table below.

And if your head isn’t spinning enough already…

…algorithms for distributed consensus need not utilise only one of these mechanisms, but may use them in combination by allocating epochs to particular methods.

Putting it all together

Paxos has been synonymous with distributed consensus for over two decades. As such, it has been extensively researched, taught and deployed in production. This thesis sought to reconsider how we approach consensus in distributed systems and challenge the widely held belief that the Paxos algorithm is an optimal solution to consensus.

Paxos was already a family of algorithms. Dr Howard has made that family considerably bigger. Algorithms now have more flexibility in their choice of quorums, values, and epochs, allowing us to make a finer-grained set of trade-offs for the situation at hand. Some of these algorithms introduce new progress properties depending on the state of the system (i.e., we are able to make progress under a broader set of conditions). One particularly interesting combination of these ideas is Multi-Paxos combined with weakened quorum intersection between phases. We can set things up to require a larger quorum for the rarely used phase one, and smaller quorums for the phase two decisions. We also have a larger set of conditions under which we can reach agreement in one round trip without centralisation.

This write-up was made considerably easier to put together by virtue of skipping all of the proofs – but of course they are all there in the thesis if you want to dig deeper!

This won’t be the last word on Paxos (the thesis has already inspired further research), but as a deconstruction and examination of the fundamentals, I fully expect it to be a reference work for a long time to come.

At the very least, we hope to have furthered understanding of this important and surprisingly subtle field of distributed systems.