CORALS: who are my potential new customers? Tapping into the wisdom of customers’ decisions

~ Adrian Colyer

CORALS: who are my potential new customers? Tapping into the wisdom of customers’ decisions Li et al., WSDM’19

The authors of this paper won round 9 of the Yelp dataset challenge for their work. The goal is to find new target customers for local businesses by mining location-based checkins of users, user preferences, and online reviews.

Location-based social networks attract millions of users to share their social friendship and their locations via check-ins. For example, an average of 142 million users check in at local businesses via Yelp every month. Foursquare and 55 million monthly active users and 8 million daily check-ins on the Swarm application. Facebook Local, powered by 70 million businesses, facilitates the discovery of local events and places for over one billion active daily users.

(And of course these are just the explicit check-ins, location tracking has proved tempting to many businesses without requiring explicit user checkin actions. For example: Facebook is tracking your phone’s location… , Google’s location history is still recording your every move…, Google tracks your movements, like it or not, …).

Check-ins give us a location history. Preference for a given business will be influenced by the proximity of that business to the places a given user frequents, in accordance with Tobler’s first law of geography: “everything is related to everything else, but near things are more related than distant things.” Which translates into:

… the propensity of a customer for a local business in inversely proportional to the distance between the customer and the business.

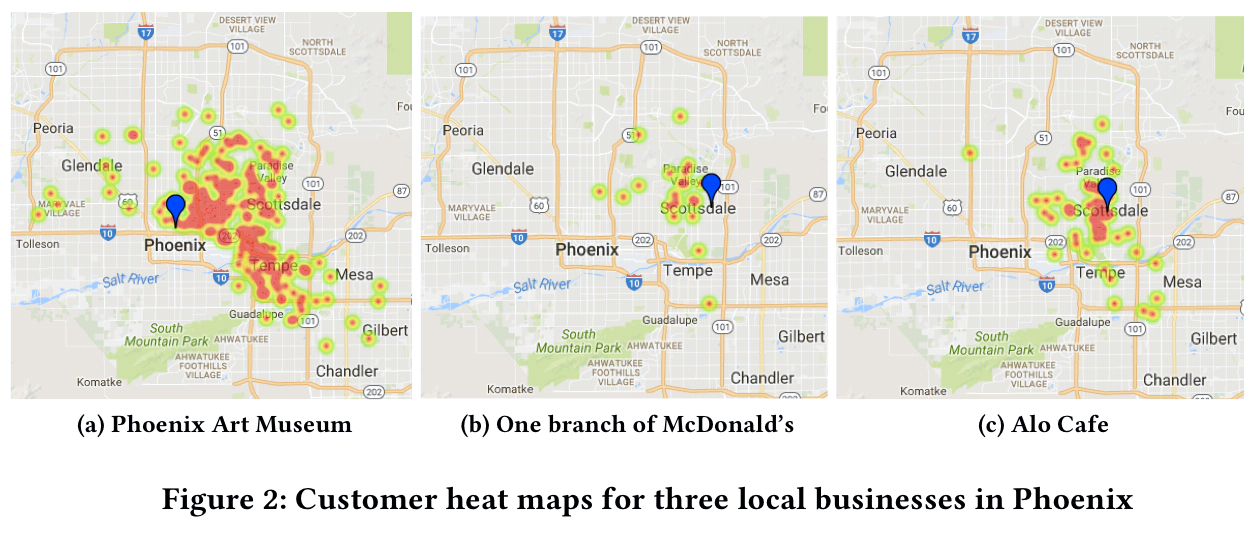
It’s not quite that straightforward though. Customers will be prepared to travel more or less far depending on the type of business. For example, customers at the Phoenix art museum travel farther to get there on average than customers at a McDonald’s.

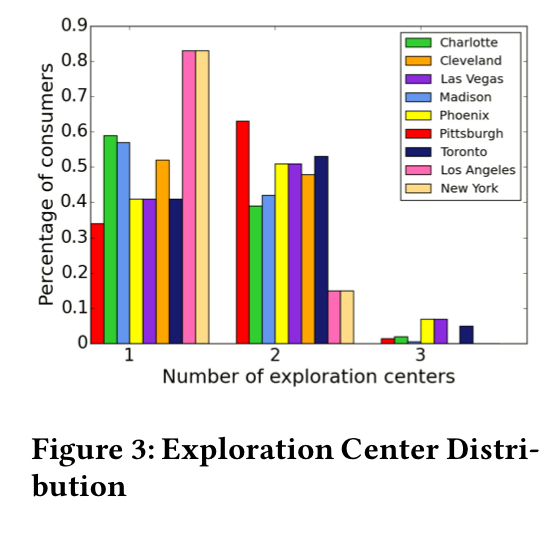
For most people, their lives gravitate around two location centres (‘exploration centres’): home and work:

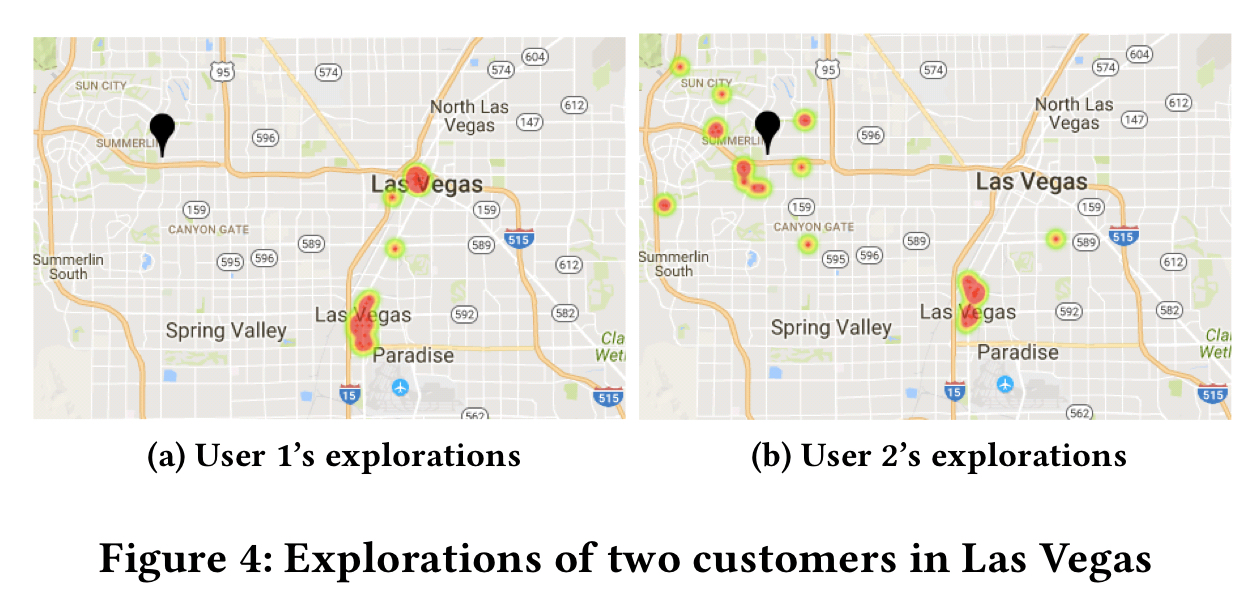
This is what that looks like for two individual users:

In addition to location and their general preferences, customers are also increasingly influenced by reviews. A 2016 study by BrightLocal found that 92% of customers regularly or occasionally read online reviews, which help them judge the quality of services offered.

… the impact of online reviews is non-negligible and growing.

One of the interesting findings from the evaluation is that to a reasonable extent, “you’re only as good as your last review!” The chart below shows a big jump in MAP when including information from the most recent review, and only a marginal performance gain with additional reviews.

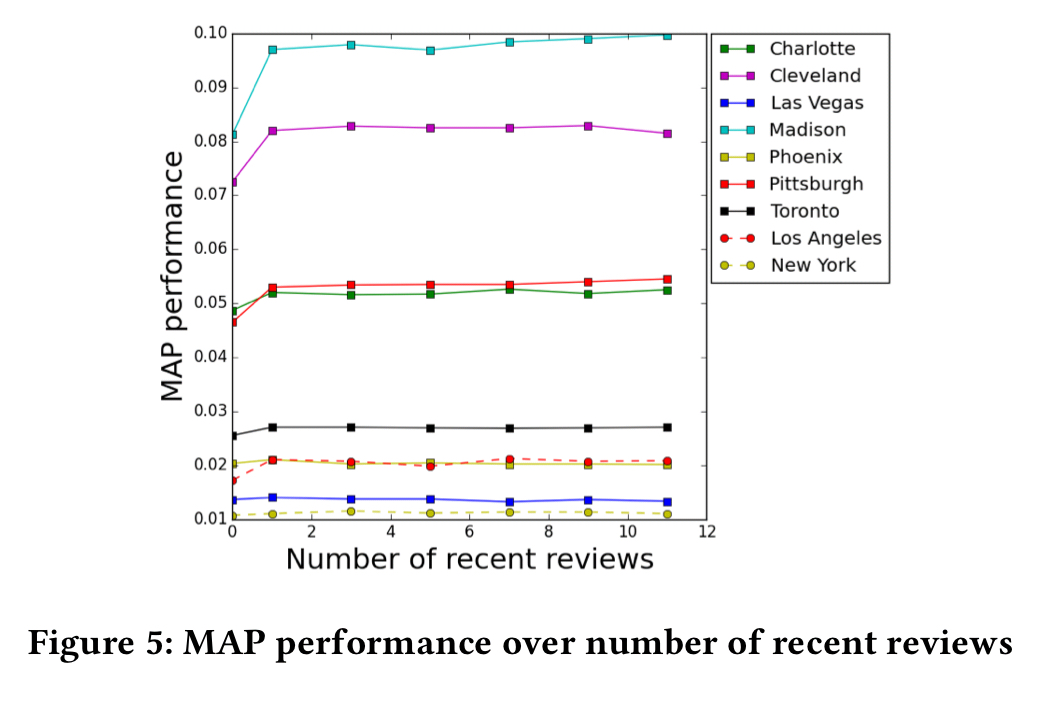
This is mainly due to the fact that customers only read a few latest reviews to perceive the reputation of the local business.

Anyway, we’re getting ahead of ourselves…

CORALS

CORALS is a customer recommendation model based on historical check-in information, which integrates customer personal preferences, geographical influence, and business reputation (reviews). These are modelled by:

  • \mathbf{t}_{b,i}, the preference of customer i for business b,
  • \mathbf{g}_{b,i}, the geographical convenience of business b for customer i
  • \mathbf{r}_{b,i}, the reliance of customer i on the reputation \mathbf{r}_b of business b

The overall tendency of a customer to visit a given business is just a linear combination of these three factors: \mathbf{t}_{b,i} + \mathbf{w}_b^g \mathbf{g}_{b,i} + \mathbf{w}_b^r \mathbf{r}_{b,i}.

The probability that a given customer will check-in at a given business location is learned by a series of pairwise comparisons. Say we know that customer i has checked in at location b. Sample another customer j at random. If j has not checked in at location b, then intuitively it ought to be that the probability for i to check in at location b should be higher than the probability of j to check in there. The probability that customer i is more likely to visit a business b than customer j is denoted by p(i >_b j|\Theta), with \Theta representing the model parameters.

It’s just a linear combination of the same three factors, but this time looking at the distances between them (and then using the sigmoid function, represented by \delta in this case, to turn the sum into a probability).

p(i >_b j|\Theta) = \delta[ (\mathbf{t}_{b,i} - \mathbf{t}_{b,j}) + \mathbf{w}_b^g (\mathbf{g}_{b,i} - \mathbf{g}_{b,j}) + \mathbf{w}_b^r (\mathbf{r}_{b,i} - \mathbf{r}_{b,i})]

The overall model is constructed by maximising over all observed and sampled checkins:

\displaystyle C = \prod_{(b,i),j} p(i >_b j|\Theta) p(\Theta)

where p(\Theta) models the parameters \Theta with a Gaussian prior.

Optimisation proceeds as follows. First the parameters \Theta are initialised using the normal distribution. Then we iterate for a fixed number of iterations, performing the following steps in each iteration:

  • For each observed check in (b, i), sample random customers j who have not visited b, making up to $latex s_{max} attempts to find a _j_ such that the preference order between _i_ and _j_ is _not_ predicted correctly.
  • If such a violation is found, update the corresponding parameter \theta \in \Theta.
  • After iterating over every observed checkin, evaluate performance on the validation set.
  • Accept the updates to \Theta from this iteration if performance has improved on the validation set, otherwise reject them.

Modelling preferences

The personal preference of customer i for business b is given by \mathbf{t}_{b,i} = \mathbf{p}_b . \mathbf{q}_i where \mathbf{p}_b and \mathbf{q}_i are business and customer vector representations in the preference hidden space. (Learned by e.g. collaborative filtering or matrix factorisation techniques).

Modelling reputations

The reliance of a customer i on the reputation of a business b is given by \mathbf{r}_{b,i} = \mathbf{u}_b . \mathbf{d}_i where \mathbf{u}_b and \mathbf{d}_i are business and customer vector representations in the reputation hidden space.

For business reputation vectors, word and sentence embeddings are used to turn review text into a vector. The n most recent reviews are used to form the final reputation vector, with n = 1 being the default. (Because ratings on a 0-5 scale weren’t available? I presume so. Someone must have studied the relative influence of words and rating numbers in online reviews… this infographic from Vendasta that turned up in a quick Google search certainly suggests stars are more important than the text).

Modelling geographical convenience

The final missing component is the geographical convenience of a business b for customer i, \mathbf{g}_{b,i}. To learn this the authors use a Gaussian mixture model taking a weighted sum over 2-vectors representing the latitude and longitude of locations visited by i. Expectation-Maximization is used to estimate the parameters of the model to maximise the likelihood of sequences of check-ins made by users.

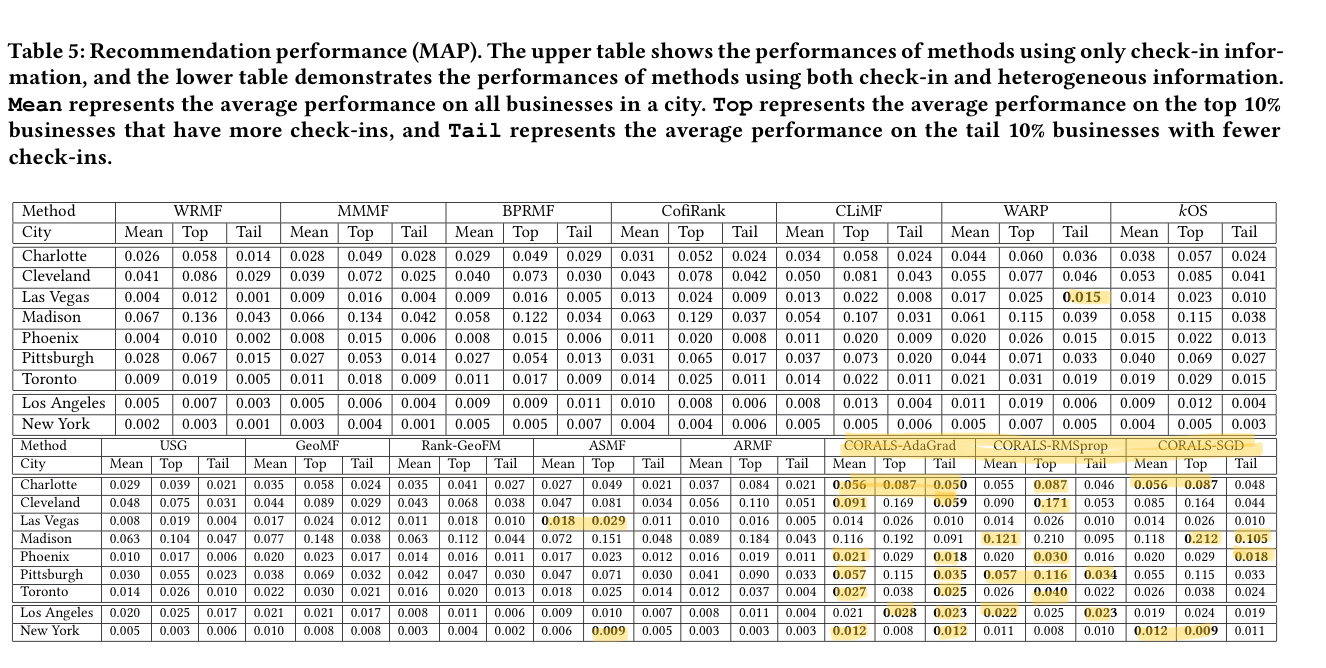
How well does it work?

The evaluation is conducted on the Yelp challenge dataset and on a Foursquare dataset. CORALS is compared against 12 other recommendation algorithms, as well as versions of itself using alternative optimisation strategies (see §3.2 for the full list).

The bottom line is that CORALS is consistently one of the top scoring models across a range of cities:

(Enlarge)

We can also see for example how geography and reputation have differing levels of influence for different kinds of businesses:

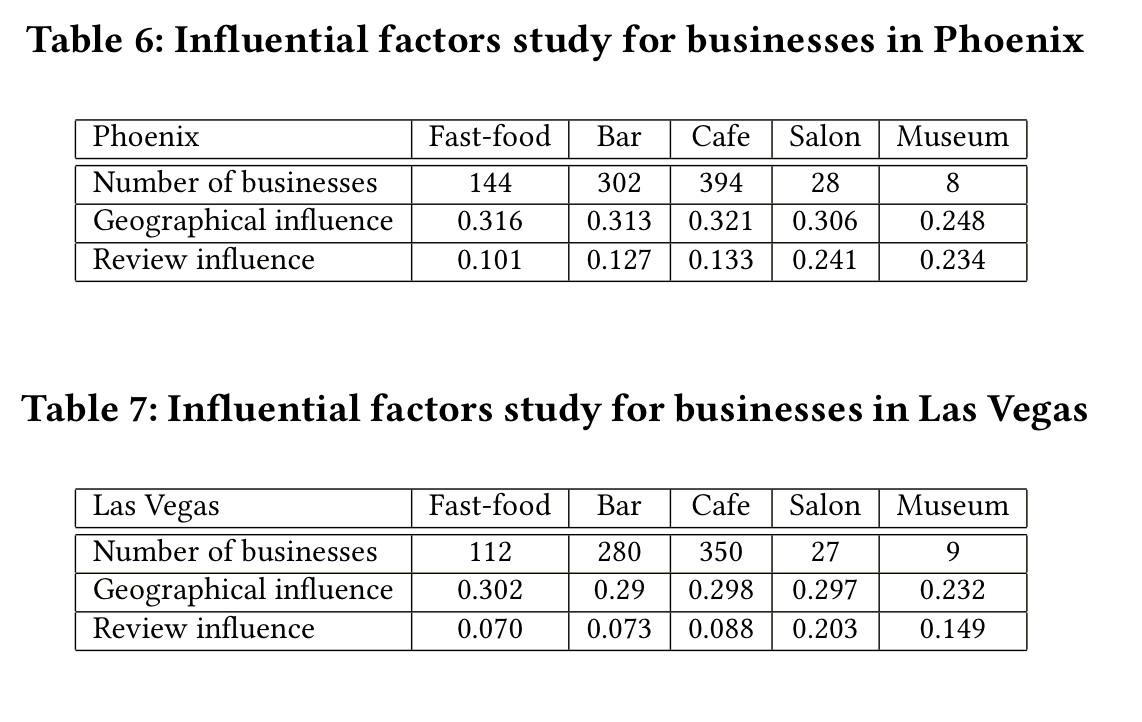
The results demonstrate that CORALS outperforms all these baselines by a significant margin in most scenarios. In addition to identifying potential new customers, we also break down the analysis for different types of businesses to evaluate the impact of various factors that may affect customers’ decisions. This information, in turn, provides a great resource for local businesses to adjust their advertising strategies and business services to attract more prospective customers.