Protecting user privacy: an approach for untraceable web browsing history and unambiguous user profiles Beigi et al., WSDM’19
Maybe you’re reading this post online at The Morning Paper, and you came here by clicking a link in your Twitter feed because you follow my paper write-up announcements there. It might even be that you fairly frequently visit paper write-ups on The Morning Paper. And perhaps there are several other people you follow who also post links that appear in your Twitter feed, and occasionally you click on those links too. Given your ‘anonymous’ browsing history I could probably infer that you’re likely to be one of the 20K+ wonderful people with a wide-ranging interest in computer science and the concentration powers needed to follow longer write-ups that follow me on Twitter. You’re awesome, thank you! Tying other links in the browsing history to other social profiles that have promoted them, we might be able to work out who else our mystery browser probably follows on social media. It won’t be long before you’ve been re-identified from your browsing history. And that means everything else in that history can be tied back to you too. (See ‘De-anonymizing web browsing data with social networks’).
In addition to the web browser, users’ browsing histories are recorded via third-party trackers embedded on web pages to help improve online advertising and web surfing experience. Moreover, Internet Service Providers (ISPs) such as AT&T and Verizon, have full access to individuals’ web browsing histories… FCC’s Internet privacy protection has also been removed in late March of 2017. This new legislation allows ISPs to monitor, collect, share and sell their customer’s behavior online such as detailed Web browsing histories without their consent and any anonymization.
(Thank goodness for the GDPR in Europe!)
Given the lack of protection, it’s now up to individual users to protect their browsing history. It’s not possible to remove entries from the history, so the only thing we can do is add noise. Adding noise may make it harder to de-anonymise a profile, and it also gives plausible deniability that you actually visited any given link that appears in the history. This is a tough one. I don’t know about you, but I feel a little uncomfortable with the thought of random links (for who knows what content!) appearing in my browsing history. Try the opposite thought experiment though, and imagine e.g. a browser plugin that posts every URL you visit to your social media feed. I don’t think many people would be comfortable with that either! The second issue with polluting your history is that some of the personalisation that goes on is actually useful. So you might start seeing content that is less relevant and interesting to you. At the heart of today’s paper is an exploration of this privacy-utility trade-off through a system called PBooster.
In this paper, we aim to study the following problem: how many links and what links should be added to a user’s browsing history to boost user privacy while retaining high utility.
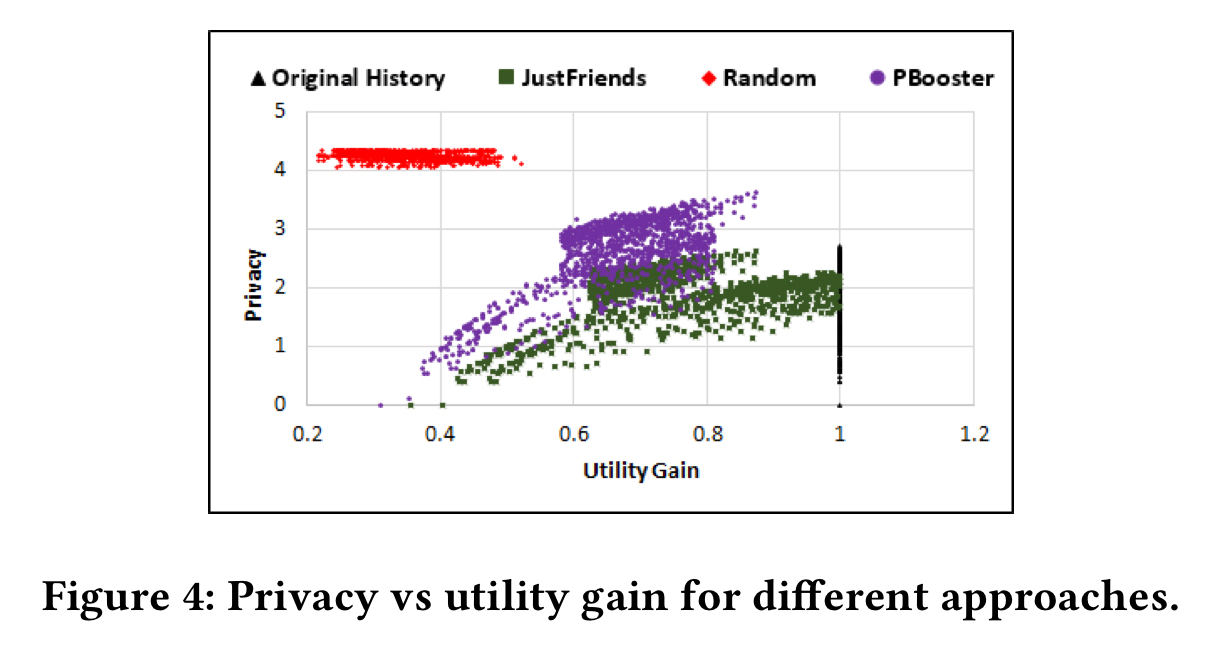
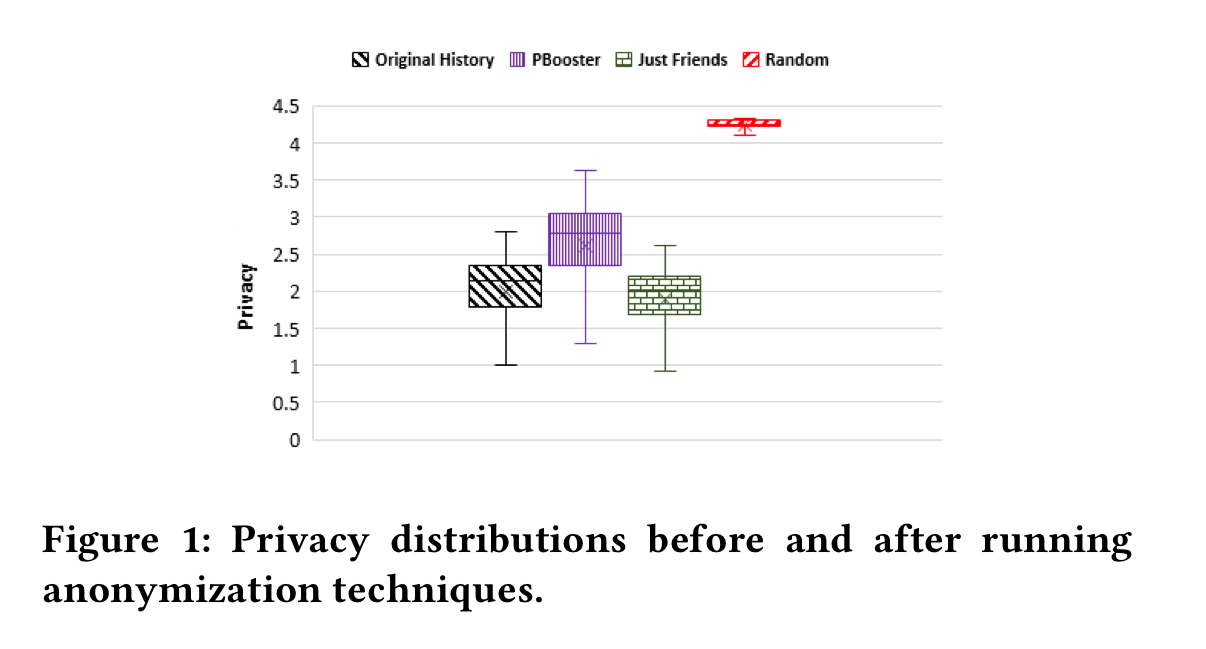
For privacy without caring about utility, just adding random links is the best strategy (though PBooster gets close).
The random link strategy seriously degrades the utility of the history though (we’ll get into how that’s measured next), whereas PBooster is able to retain much more utility.
Measuring privacy and utility
From a privacy perspective, the more uniformly distributed a history is over a set of topics, the harder it will be to infer which topics are of true interest. Thus,
… we leverage the entropy of the user’s browsing history distribution over a set of pre-defined topics as a measure of privacy.
Given some set of m topics, we assign each link in the browsing history to one of those topics, sum counts when grouping by topic, and then normalise them to give the topic probability distribution. Using j to range over topics, 
The higher this metric is, the greater the privacy.
For utility, we want the opposite: a similar distribution between the modified history, 
For this work cosine similarity is used:
Navigating the privacy-utility trade-off with PBooster
PBooster seeks to optimise an objective function 
It is worthwhile to mention that the search space for this problem is exponential to
, where N is the maximum number of links with respect to a topic.
That’s about as bad as it gets!
The solution is to break the search down into two subproblems: first select a subset of topics, and calculate how many links should be added to each (the topic selection phase, and then select the links for each topic (link selection phase).
An analysis in section 4.4 of the paper shows that the topic selection process is also NP-hard, but there exists a greedy local search algorithm which can achieve at least 1/3 of the value of the optimal solution. The algorithm alternates between incrementing the link counts of topics and decrementing them, until no further improvement is possible.
We emphasize that according to [13], there is no efficient algorithm which could select the best set of links to maximize aggregation of both privacy and utility in polynomial time… the proposed greedy algorithm can select a set with a lower bound of 1/3 of the optimal solution, providing the maximum user privacy and utility in polynomial time.
When it comes to selecting actual links to hit the desired topic counts, PBooster needs access to the user’s friend list on social media. It randomly selects a social media profile from outside of your friend list, and simulates a browsing history from that profile for links in the desired topic areas. If the chosen social media profile does not contain enough such links, another profile is chosen at random until all link count targets are hit.
Evaluation
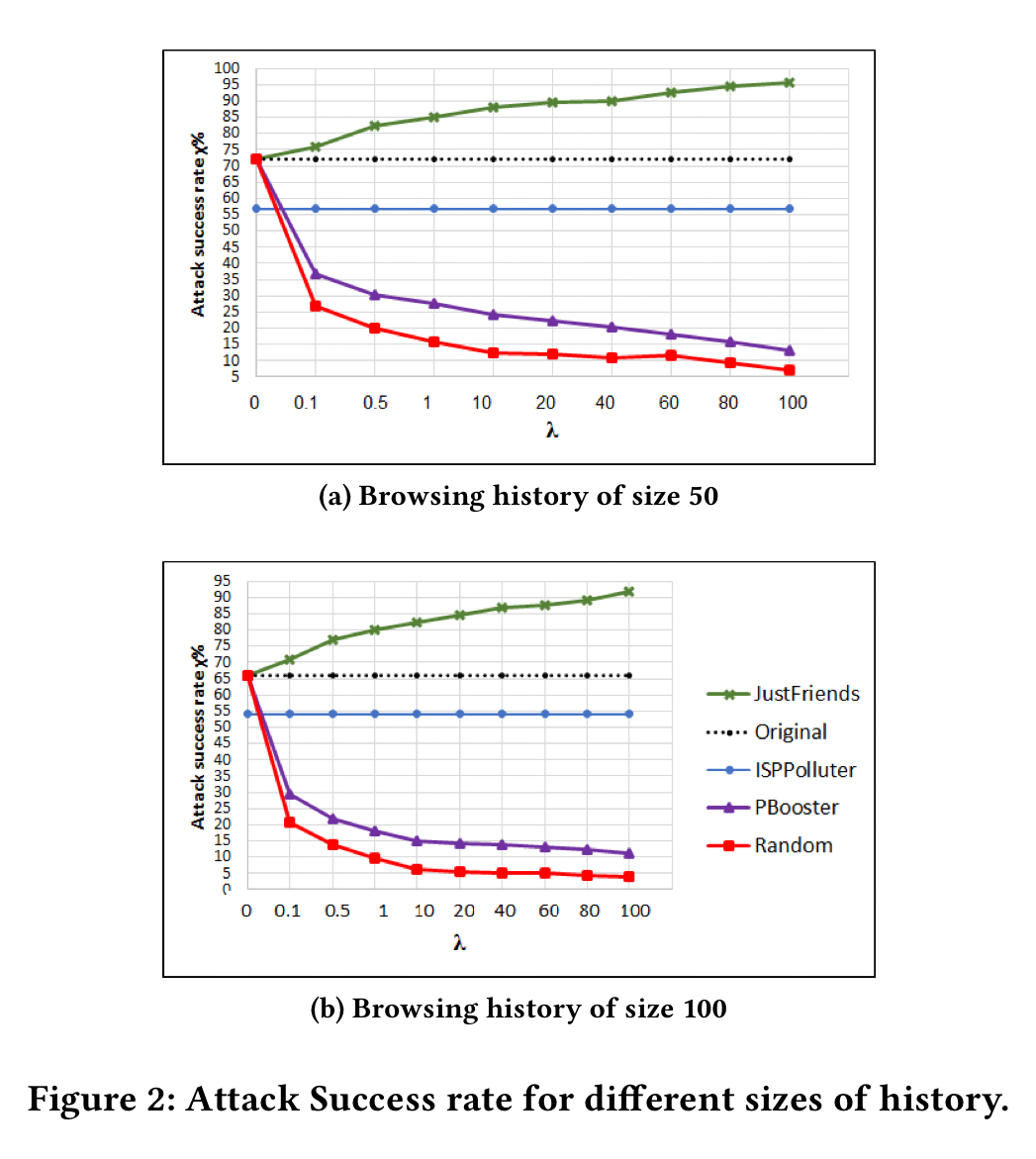
The evaluation compares PBooster against a strategy of adding the total number of links recommended by the topic selection phase but at random with no consideration for topics, a ‘JustFriends’ strategy that adds links from the profiles of friends during the link selection phase, and an ‘ISPPolluter’ strategy that adds 20,000 links randomly to the history.
As we saw previously, since random strategies pay no attention to utility, they can achieve the best overall privacy:
Interestingly, ISPPolluter turned out not to work well in practice as a defense against attacks that leverage information from social media feeds. For intuition, consider that even adding 20,000 random links, a history with say 50 visits to The Morning Paper is still going to be pretty unique (that is very unlikely to happen by chance). Whereas when links are added from a social media profile, this kind of behaviour is generated by design. However, as I understand it the end result of using PBooster will be a history that instead of containing influences from n social media profiles, will now contain influences from n+m profiles, where m is the number of profiles used during the link selection phase. The measure used for privacy only looks at topic distribution, not the end number of influencing profiles. I’d really like to see some analysis of this aspect (for example, if m is small compared to n, then the user is probably still very identifiable, so how should we think about m as it relates to n?).
When it comes to balancing the trade-off between utility and privacy as measured though, PBooster unsurprisingly comes out best.
Our experiments demonstrate the efficiency of the proposed model by increasing user privacy and preserving utility of browsing history for future applications.