ApproxJoin: approximate distributed joins Le Quoc et al., SoCC’18
GitHub: https://ApproxJoin.github.io
The join is a fundamental data processing operation and has been heavily optimised in relational databases. When you’re working with large volumes of unstructured data though, say with a data processing framework such as Flink or Spark, joins become distributed and much more expensive. One of the reasons for this is the amount of data that needs to be moved over the network. In many use cases, approximate results would be acceptable, and as we’ve seen before, likely much faster and cheaper to compute. Approximate computing with joins is tricky though: if you sample datasets before the join you reduce data movement, but also sacrifice up to an order of magnitude in accuracy; if you sample results after the join you don’t save on any data movement and the process is slow.
This paper introduces an approximate distributed join technique, ApproxJoin, which is able to sample before data shuffling without loss of end result accuracy. Compared to unmodified Spark joins with the same sampling ratio it achieves a speedup of 9x while reducing the shuffled data volume by 82x.
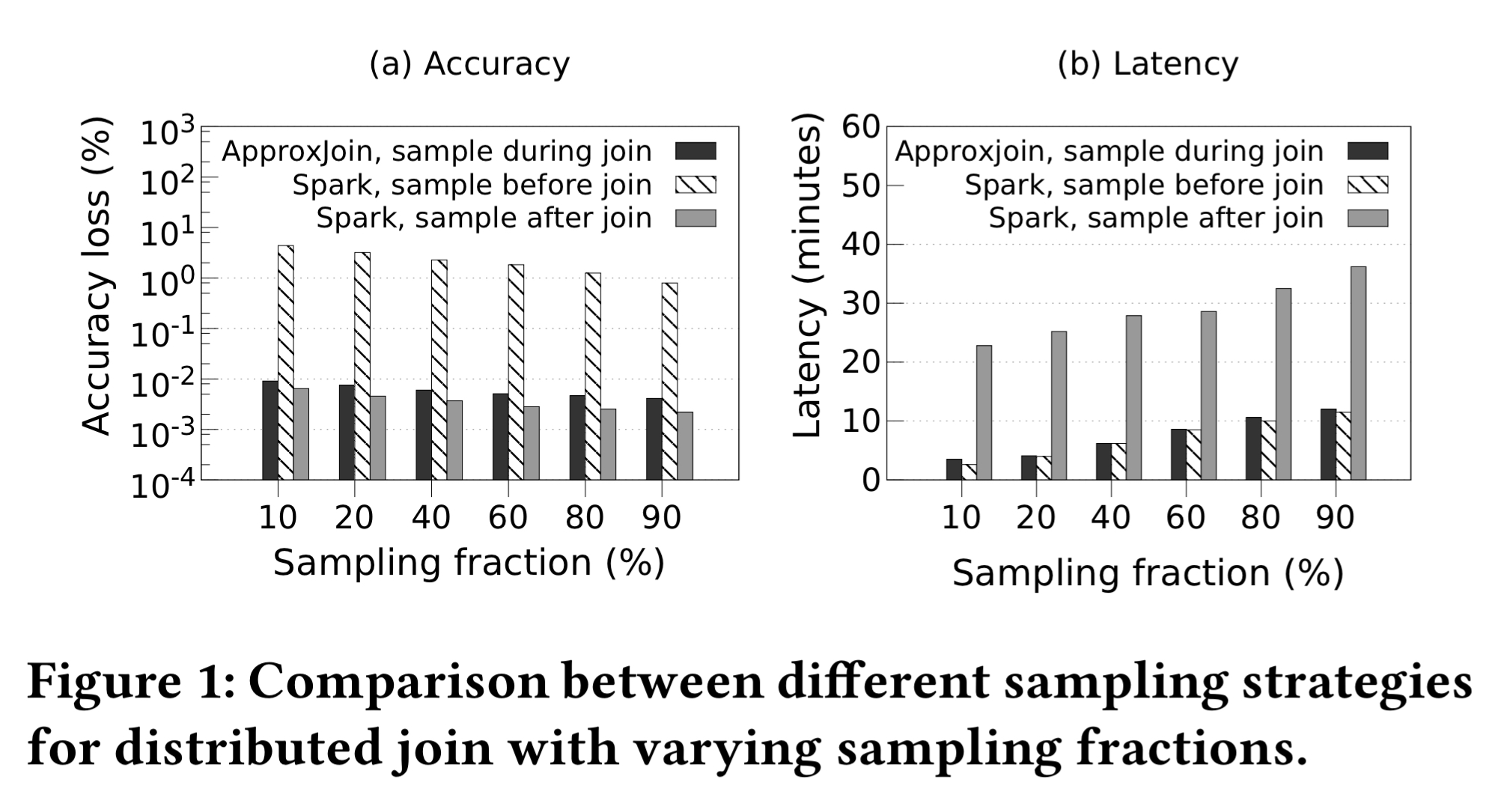
The following charts show ApproxJoin’s latency and accuracy characteristics compared to Spark sampling before the join (ApproxJoin has much better accuracy and similar latency) and to Spark sampling after the join (ApproxJoin has similar accuracy and much lower latency).
ApproxJoin works in two phases. First it uses one of the oldest tricks in the book, a Bloom filter, to eliminate redundant data shuffling. A nice twist here is that ApproxJoin directly supports multi-way joins so we don’t need to chain a series of pairwise joins together. In the second phase ApproxJoin uses stratified sampling to produce an answer approximating the result of an aggregation over the complete join result.
At a high level, ApproxJoin makes use of a combination of sketching and sampling to select a subset of input datasets based on the user-specified query budget. Thereafter, ApproxJoin aggregates over the subset of input data.
User queries must contain an algebraic aggregation function (e.g. SUM, AVG, COUNT, STDEV), and as is usual for approximate compute frameworks, can specify either a time bound or an error bound for the query.

High level overview
Overall, the ApproxJoin system looks like this:
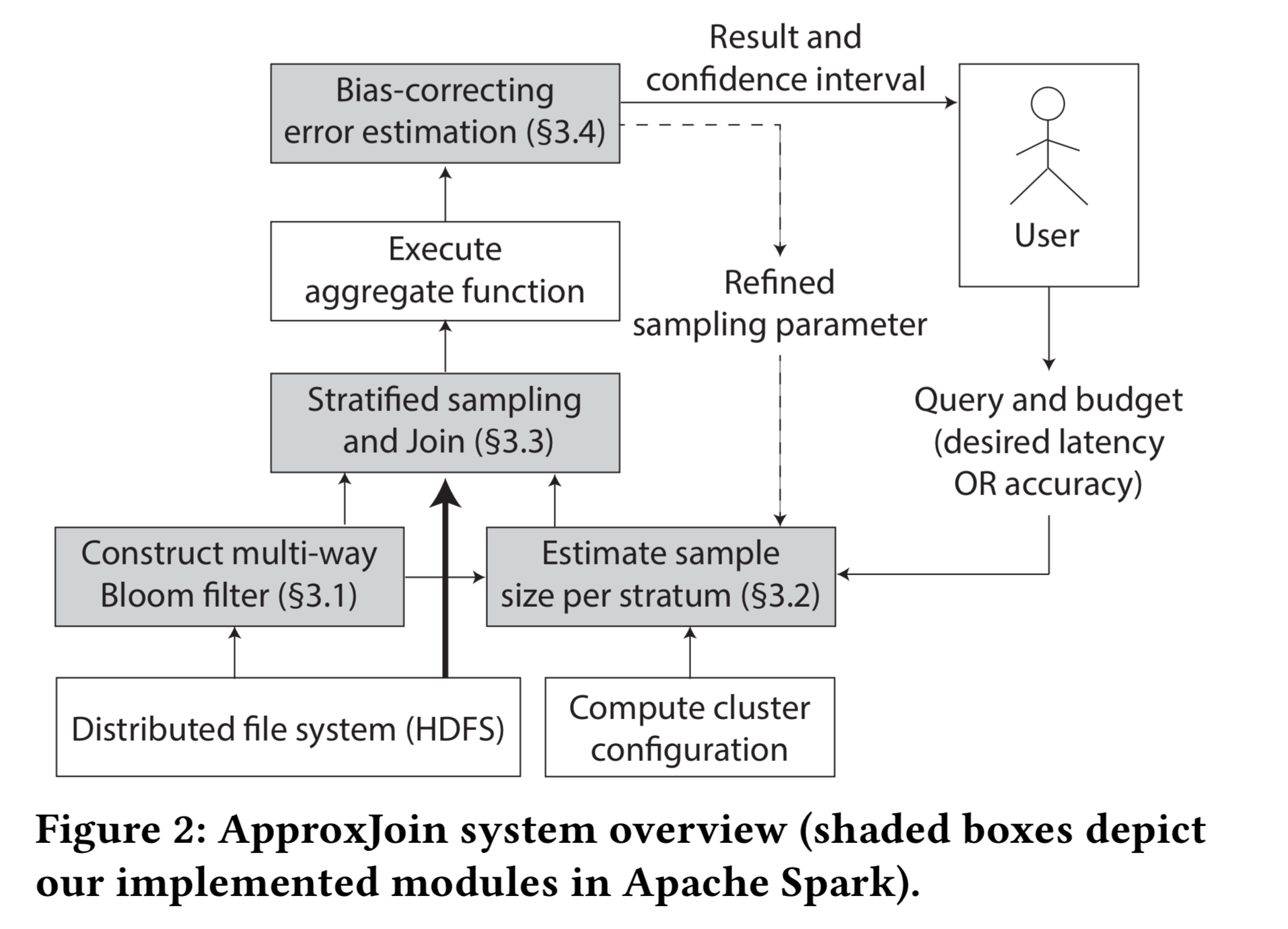
Filtering using a multi-way Bloom filter happens in parallel at each node storing partitions of the input, and simultaneously across all input tables.
The sampling phase makes use of stratified sampling within the join process: datasets are sampled while the cross product is being computed. Stratified sampling in this case means that tuples with distinct join keys are sampled independently (with simple random sampling). Thus the final sample will contain all join keys— even those with few data items. A cost function is used to compute an optimal sampling rate according to the query budget. There’s a one-off upfront cost to compute the standard deviation for a join key (‘stratum’), which is stored and reused in subsequent queries. It’s not clear whether or not this cost is included in the evaluation (so best guess it isn’t 😉 ).
Filtering
The filtering step is very straightforward. First a Bloom filter is created for each input dataset: each worker with a partition of the dataset creates a local bloom filter, and then these are combined using OR. Once we have the merged Bloom filter for each input dataset, we can simply combine the filters across datasets using AND. (Think about hashing a given key, only if the corresponding bits are set in each of the input Bloom filters can that key possibly exist in all inputs). In the implementation, Bloom filters are merged using a treeReduce scheme to prevent the Spark driver becoming a bottleneck.
Clearly, the greater the overlap between the input datasets the more data we need to shuffle, and hence the less benefit the Bloom-filter based join can add.
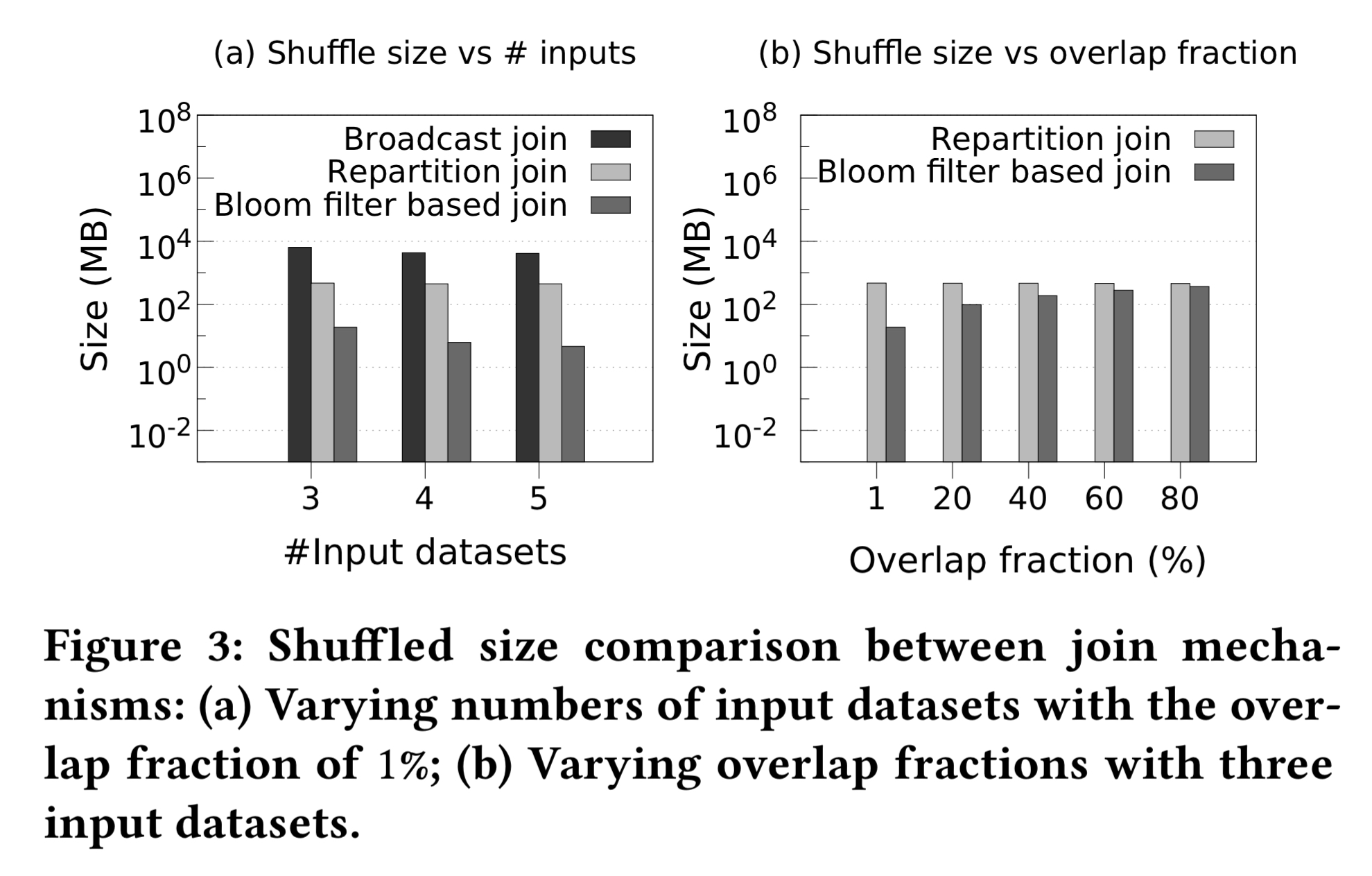
After the filtering stage, it may be that the overlap fraction between the datasets is small enough that full join can now be performed within the latency requirements of the user. If this is not the case, we proceed to the approximation…
Determining the cost function
ApproxJoin makes use of latency and error-bound cost functions to convert the join requirements specified by a user into sampling rates.
For the latency cost function we need to combine the cost of filtering and transferring the data join items, with the cost of computing the cross products. There’s no need to estimate the cost of filtering and transferring— we have to do this regardless so we can just time it. The remaining latency budget is simply then the target time specified by the user, minus the time we spent in the first phase! The cost function for the cross product phase is simply a weighting of the number of cross products we need to do. The weighting (scale) factor depends on the computation capacity of the compute cluster, which is profiled once offline to calibrate. (That is, once in the lifetime of the cluster, not once per query).
If a user specified an error bound, we need to calculate how many samples to take to satisfy the requirement. For stratum i, the number of samples turns out to be governed by the following equation at 95% confidence level:
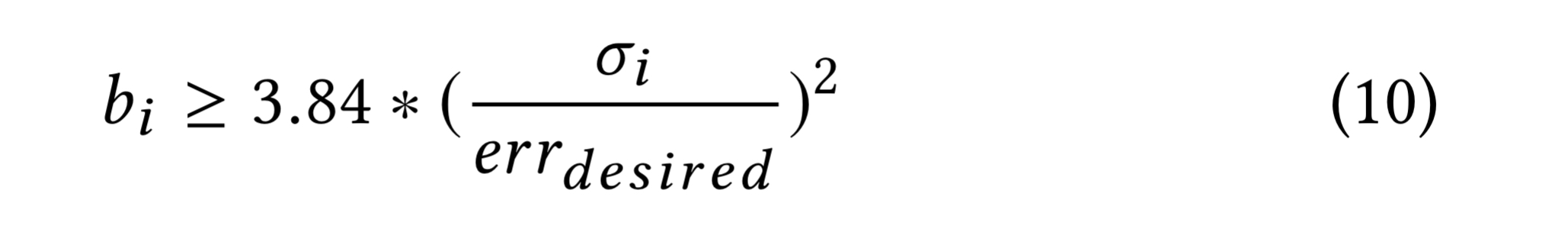
The standard deviation of the stratum is computed and stored on the first execution of a query and subsequently reused.
Sampling
To preserve the statistical properties of the exact join output, we combine our technique with stratified sampling. Stratified sampling ensures that no join key is overlooked; for each join key, we perform simple random selection over data items independently. This method selects data items fairly from different join keys. The (preceding) filtering stage guarantees that this selection is executed only from data items participating in the join.
Random sampling on data items having the same join key is equivalent to perform edge sampling on a complete bipartite graph modelling the relation.
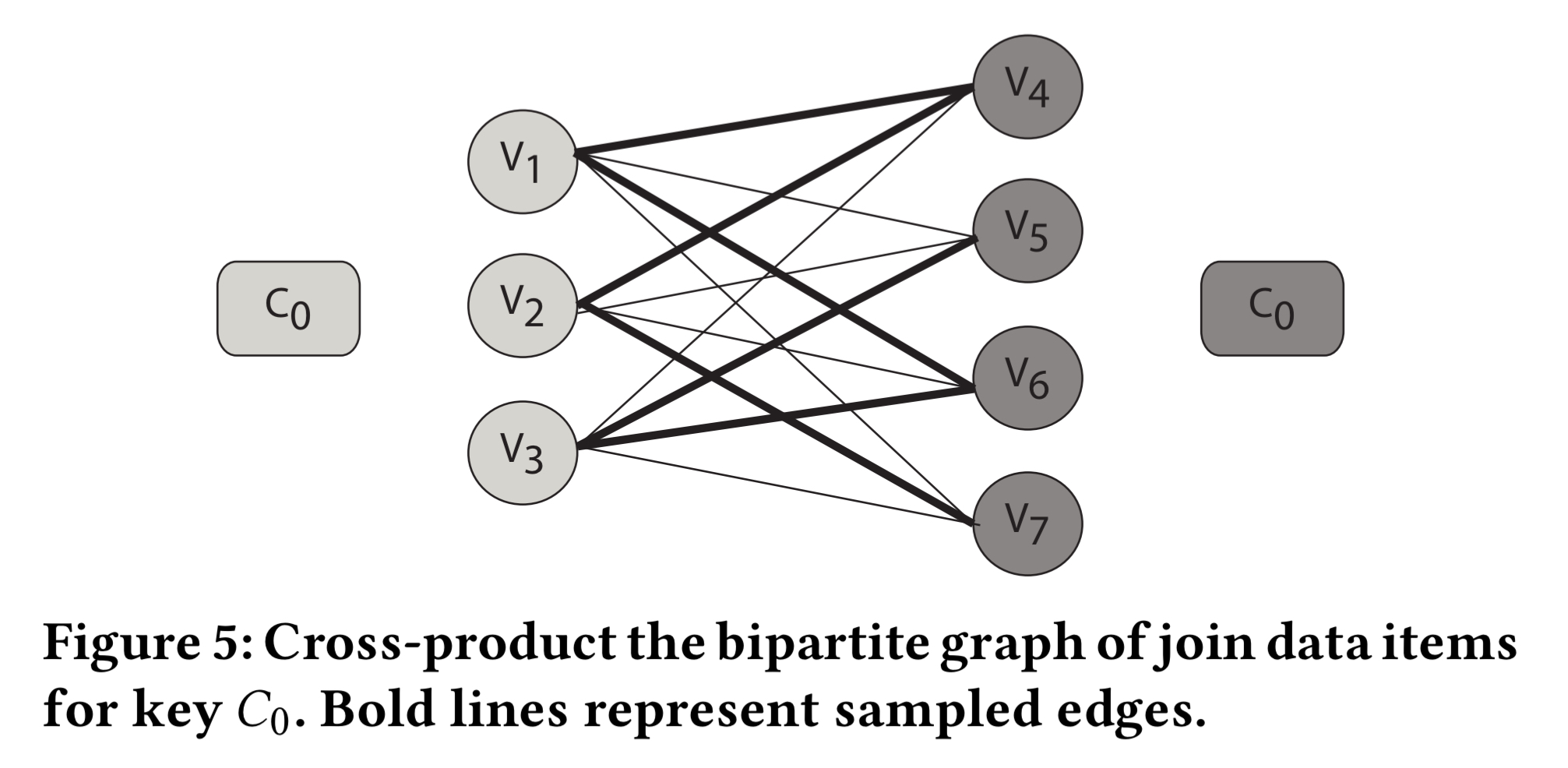
To include an edge in the sample, ApproxJoin randomly selects one endpoint vertex from each side, and then yields the edge connecting them. For a sample of size b this process is repeated b times.
In a distributed settings, data items are distributed to worker nodes based on the join keys (e.g. using a hash-based partitioner), and each worker performs the sampling process in parallel to sample the join output and execute the query.
Query execution
After sampling, each node executes the input query on the sample to produce a partial query result. These results are merged at the master node, which also produces error bound estimations.
Estimating errors
The sampling algorithm can produce an output with duplicate edges. This acts as a random sampling with replacement, and the Central Limit Theorem can be used to estimate the error bounds. An alternative error estimation mechanism is also described in which duplicate edges are not allowed in the sample, and a Horvitz-Thompson estimator can be used. I couldn’t determine which of these two mechanisms is actually used for the results reported in the evaluation.
Evaluation
Focusing just on the filtering stage to start with, we see that with two-way joins ApproxJoin is 6.1x faster than a native Spark join, and shuffles 12x less data. The gains are even better with 3-way and 4-way joins:
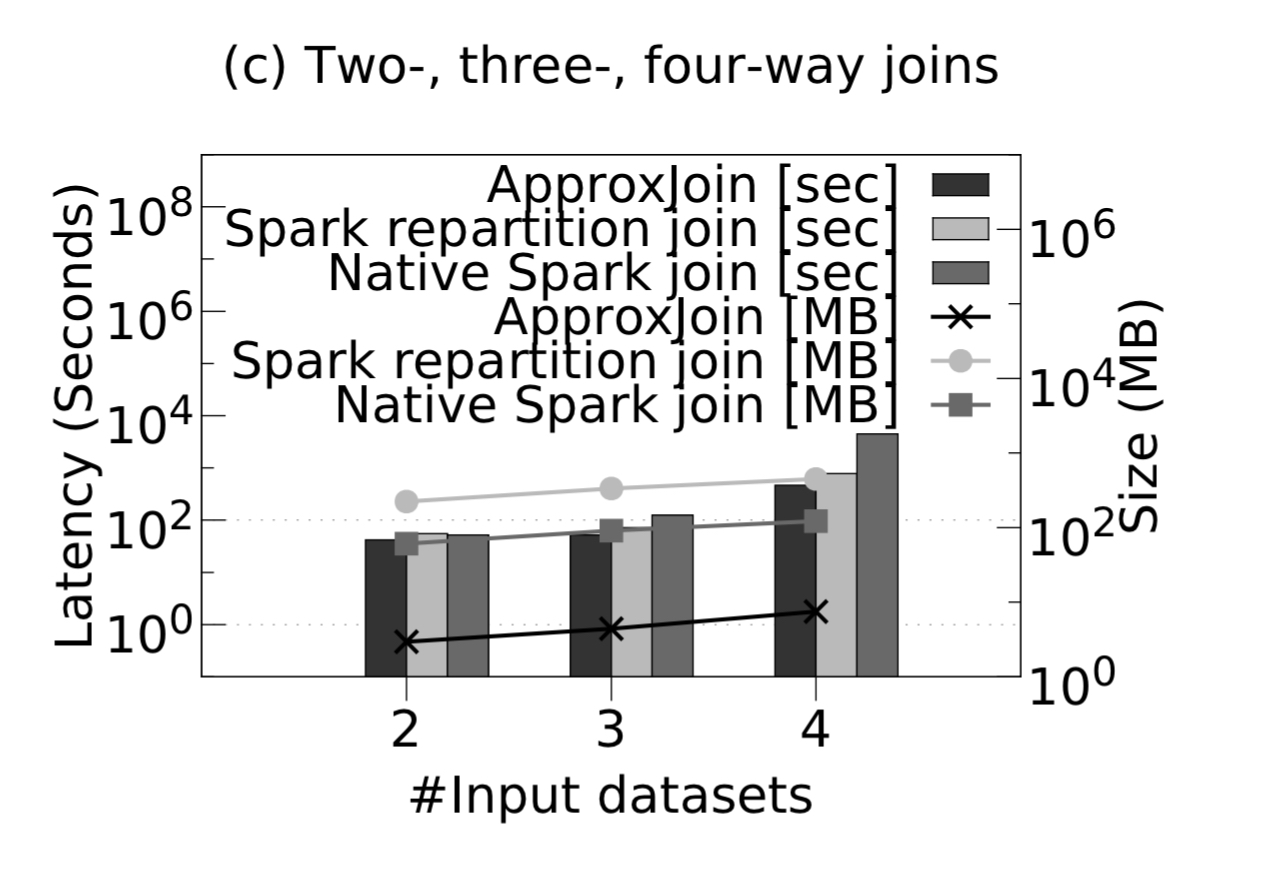
The benefits do depend on the overlap percentage though. The figures above were all with overlap fractions below 1%, and the ApproxJoin advantage disappears by the time we get to around 8%.
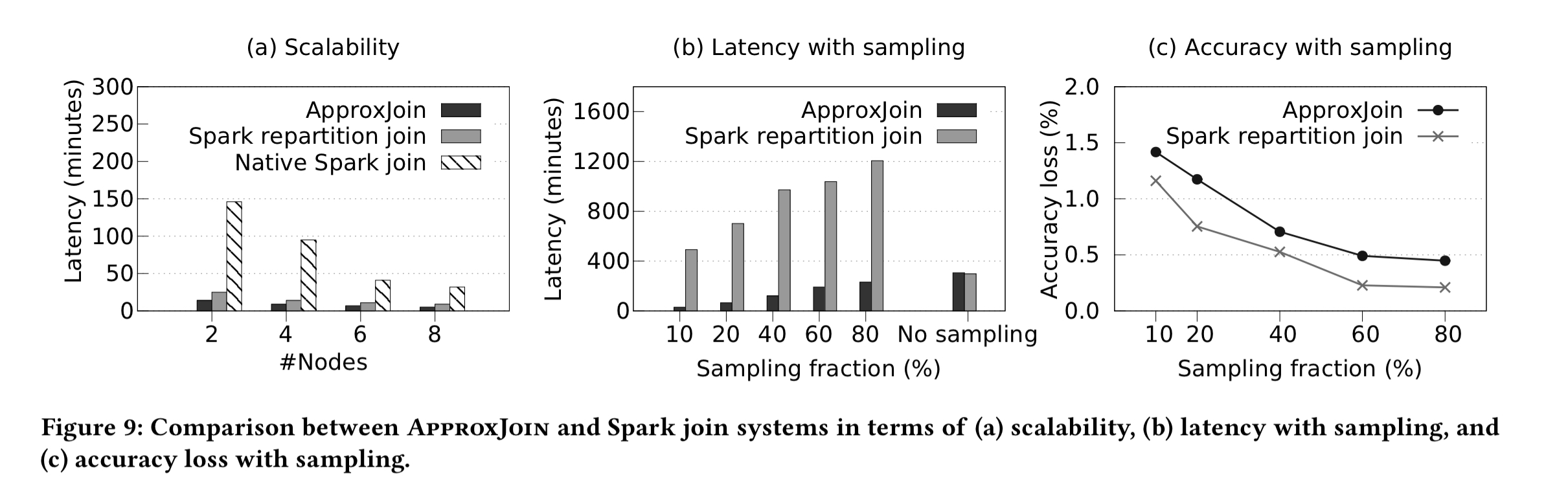
Turning to the sampling stage, the following figure compares scalability, latency, and accuracy of ApproxJoin sampling vs Spark joins. Here ApproxJoin can deliver order of magnitude speed-ups.
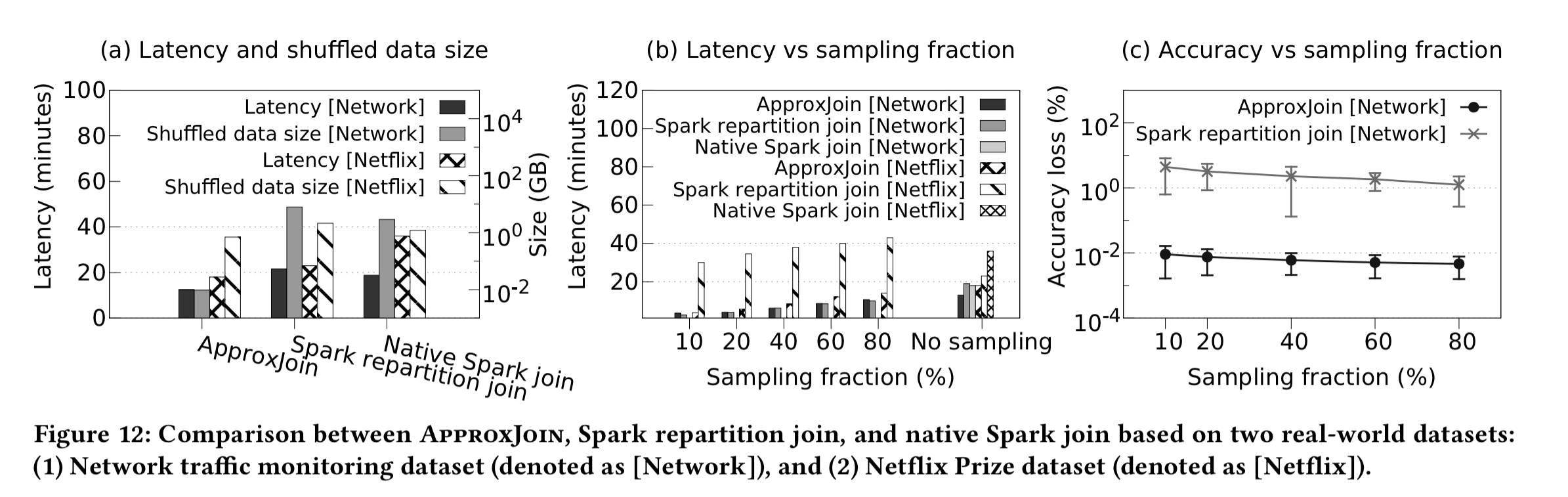
ApproxJoin is also evaluated end-to-end on two real-world datasets: CAIDA network traces, and the Netflix prize dataset. For the network trace dataset ApproxJoin is 1.5-1.7x faster, and reduces shuffled data by 300x. For the Netflix dataset ApproxJoin is 1.27-2x faster, and shuffles 1.7-3x less data.
By performing sampling during the join operation, we achieve low latency as well as high accuracy… Our evaluation shows that ApproxJoin significantly reduces query response time as well as the data shuffled through the network, without losing the accuracy of the query results compared with the state-of-the-art systems.