Oblix: an efficient oblivious search index Mishra et al., IEEE Security & Privacy 2018
Unfortunately, many known schemes that enable search queries on encrypted data achieve efficiency at the expense of security, as they reveal access patterns to the encrypted data. In this paper we present
Oblix, a search index for encrypted data that is oblivious (provably hides access patterns) is dynamic (supports inserts and deletes), and has good efficiency.
There’s a lot to this paper! Starting with a recap of existing work on Path ORAM (Oblivious RAM) and Oblivious Data Structures (ODS), Mishra introduce an extension for an Oblivious Sorted Multimap (OSM) (such that you can look up a key and find a set of associated values, handy for building indexes!). Then because their design runs a client-proxy process inside an enclave at the server, and enclaves still leak some information, they also design “doubly-oblivious” versions of all of the above that hide the client access patterns in addition to those at the server process. It’s all topped off with an implementation in Rust (nice to see Rust being used for systems research), and an evaluation with three prime use cases: private contact discovery in Signal, private public key lookup based on Google’s Key Transparency, and a search index built over the entire Enron email dataset.
We show that Oblix can scale to databases of tens of millions of records while providing practical performance. For example, retrieving the top 10 values mapped to a key takes only 12.7ms for a database containing ~ 16M records.
It’s a good reminder that some of the things we often accept as ‘obviously true,’ such as that an app which wants to tell you what’s nearby must track your location, aren’t necessarily so.
It’s impossible to cover it all in my target post length, but I’ll do my best to give you a feel for the work.
Motivation and high-level design
A server holds an encrypted database, and a client wants to retrieve matching records by key from that database, without leaking information about their access patterns. For example, in the Signal messaging system a user can query to determine which of the their phone contacts also use Signal, and this needs to be done in such a way that Signal never learns the user’s contact list. Beyond access patterns, it is also important to hide the result size.
In Path ORAM the client is responsible for maintaining a position map (index) and a stash of temporary values. When the database gets too big for the client to store (e.g., all of Signal’s contacts) it is possible to add one or more intermediate ORAM servers. With one intermediary for example the client maintains a smaller index of positions in the intermediary, which then knows the true positions in the server. Each index lookup therefore requires a logarithmic (in index size) number of requests.
Using hardware enclaves (e.g. SGX), Oblix resolves this multiple roundtrip problem by placing ORAM clients in enclaves on the same server as the ORAM server. On its own, just using an enclave isn’t good enough for the privacy standards we’re aiming at here:
Recent attacks have shown that hardware enclaves like Intel SGX leak access patterns in several ways… For Path ORAM, this means that if the attackers sees accesses to the client’s position map or stash, it can infer access patterns to the ORAM server, defeating the purpose of using ORAM.
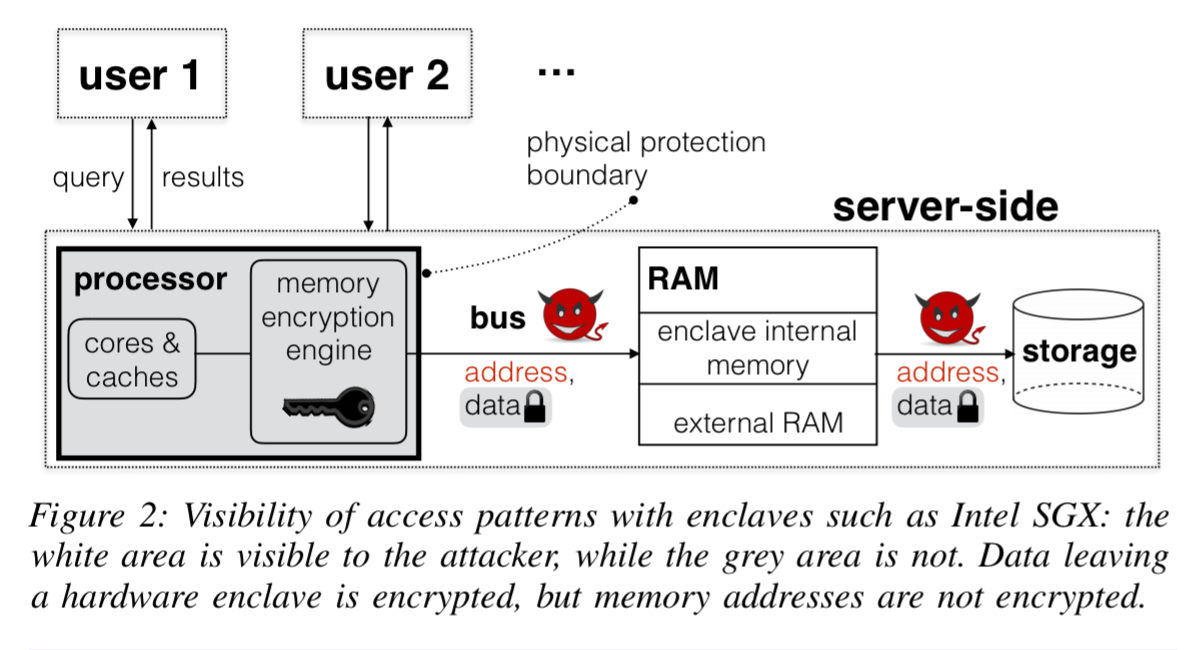
To get around these leaks, Oblix also uses ORAM techniques inside the client proxy process as well, resulting in doubly oblivious schemes. Hiding result set sizes requires in the basic case that every returned result set is padded to the size of the maximum possible result set. That clearly introduces a lot of overhead! Oblix is designed to work with result pages (e.g., top 20 results), which caps the amount of padding to the page size. This in turn means that the scoring information must also be contained within the index data structure, for which we need an efficient oblivious structure for ordered list values. That’s where the the doubly oblivious sorted multimap (DSOM) comes in.
(Singly) Oblivious Data Structures
Path ORAM essentials
Path ORAM is an ORAM protocol allowing a client to perform oblivious reads and writes to external server memory with low bandwidth and latency. The server maintains a binary tree containing C buckets of B bits each. The client maintains a position map from block id to leaf node, such that the associated block can be found an a path from the root node to that leaf. The client also maintains a stash – think of it like a small cache of blocks – that the server populates and the client may modify. For example, a read request from the client contains a block id, leaf id, and the stash. ORAM.ReadBlock with fetch all blocks on the path to the given leaf id and put them in the stash, outputting the block in the path with the given id. The block is also assigned a new random leaf in the positions map for future accesses.
The Oblivious Data Structures (ODS) framework
The Oblivious Data Structures framework lets you design oblivious data structures that can be expressed as trees of bounded degree. So long as you can express the desired functionality via such an abstraction you’re good to go. Oblivious data structures work with an underlying ORAM scheme, such as Path ORAM. There are three rules:
- Every node must have a unique predecessor (a node pointing to it) [Excepting the root node I presume!]
- Every operation accesses a unique root node before any other node
- Every operation accesses a non-root node’s predecessor before it accesses the node.
In short: there’s a tree of nodes, and every operation walks the tree starting at the root.
Oblivious sorted multimaps
Our oblivious sorted multimap (OSM) enables a client to outsource a certain type of key-value map to an untrusted server so that the map remains encrypted and, yet, the client can still perform search, insert, and delete operations with small cost (in latency and bandwidth) without revealing which key-value pairs of the map were accessed. This notion extends previous notions such as oblivious maps.
An OSM scheme contains init, find, insert, delete, and server protocol algorithms. At a high level it supports a mapping from a key to a possible empty list of sorted and distinct values. The authors realise their scheme using the ODS framework, which involves first constructing a plaintext data structure with tree-like memory accesses, and then replaces those accesses with the oblivious counterparts defined by the ODS framework.
The solution to this challenge combines ideas from AVL search trees and order statistic trees. In an order statistic binary search tree, each node also stores the number of nodes in each (left and right) child subtree, and this is used to find the the node with the i-th smallest key. The OSM scheme modifies this idea such that a node with key k also stores the number of nodes in each of its child subtrees that also have key k. Using this we can efficiently find a key’s i-ith value, and also therefore any sublist of values.
We remark that our OSM construction above (coupled with padding as discussed below) already provides a search index that does not leak access patterns without relying on hardware enclaves: the client stores the OSM state locally and interacts with the remote server over the network for each OSM operation. Leveraging hardware enclaves will enable better performance and support for multiple users.
Doubly Oblivious Data Structures
When the ORAM client runs at a server, it’s memory accesses are visible to the server (even when inside an enclave), and that leaks information. The authors introduce doubly oblivious RAM (DORAM) client algorithms for Path ORAM, ODS, and OSM schemes. We pay a time complexity for this additional obliviousness, as summarised in the following table.
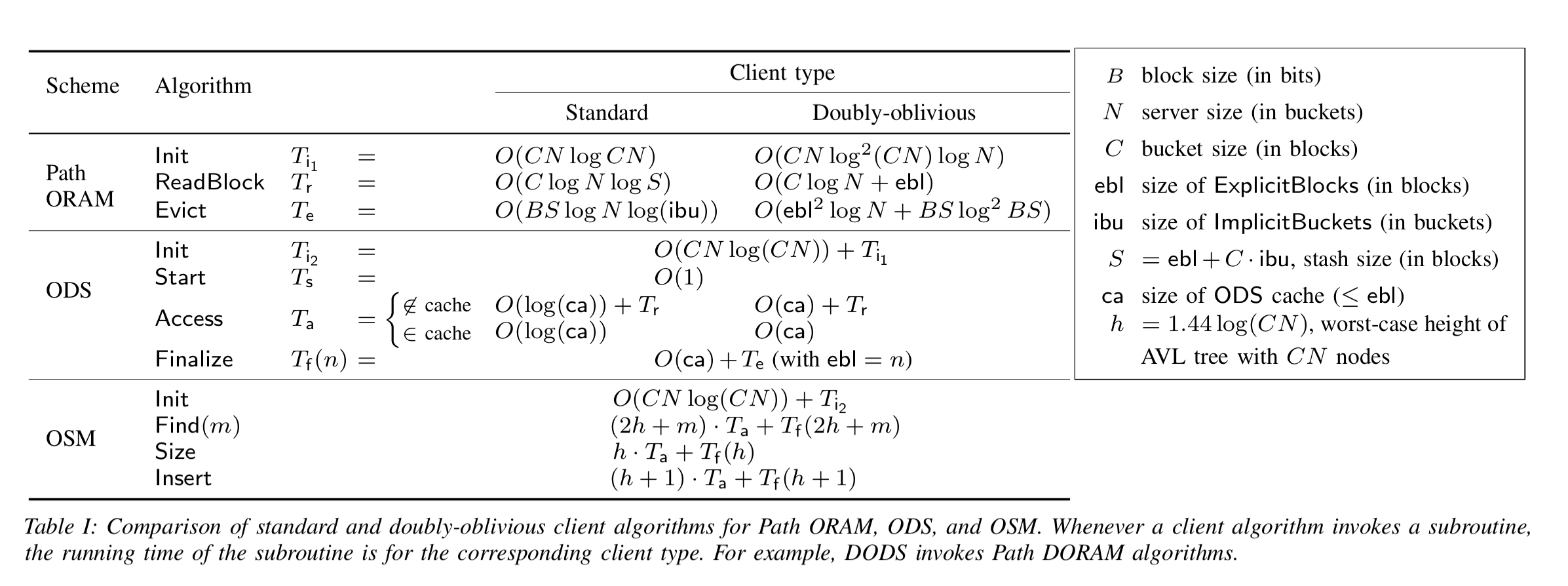
(Enlarge)
Path DORAM
A simple but inefficient client scheme for Path ORAM would be to replace all suitable sub-routines (such as binary search) with linear scans. Splitting eviction into two steps (first assigning blocks, and then writing blocks) reduces the naive time by a factor of C (number of buckets in the tree). Details are in section V.A.
Doubly-oblivious data structures (DODS)
Replacing the underlying ORAM scheme for ODS with a doubly-oblivious one is not sufficient to make a doubly-oblivious ODS (DODS) since an adversary can still learn some information by observing whether a returned node is fetched from the cache or from external memory. Always doing a (possibly) dummy external read solves this issue at the expense of performance. DODS mitigates this cost somewhat by only doing the additional read when an observer could not already know for certain whether or not a node is in the cache.
Doubly-oblivious sorted multimaps
The doubly-oblivious sorted multimap (DOSM) can now be built on top of DODS. This on its own is not sufficient, since accesses to the OSM internal state (outside of the ODS framework) can still be leaked.
To eliminate such leakage, we identify data-dependent sub-procedures of our algorithms, and appropriately pad out the number of accesses made in these procedures to worst-case bounds that depend only on the number of key-value pairs in the map… Next we design our algorithms so that we can always predict whether or not a given dummy access needs to return a cached node. We can then take advantage of the fine-grained DODS interface to avoid unnecessary dummy operations.
Evaluation
It takes about 10K lines of Rust code to implement singly and doubly oblivious version of Path ORAM, ODS, and OSM.
For the Signal contacts use case, Oblix can enable private contact discovery with latency 
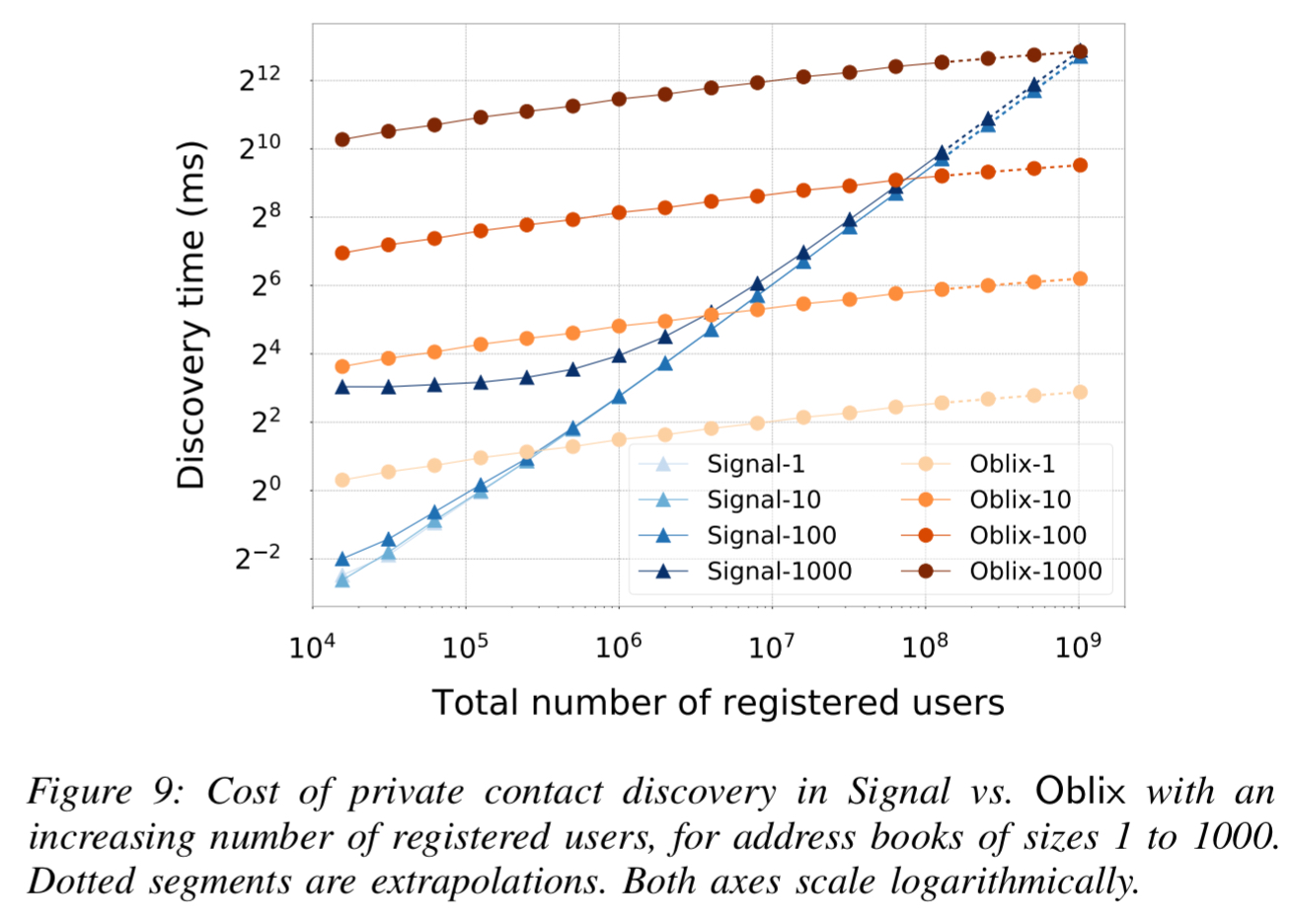
The Oblix approach really shines with incremental contact discovery where smaller values of m (e.g. 10 or less) are much more common.
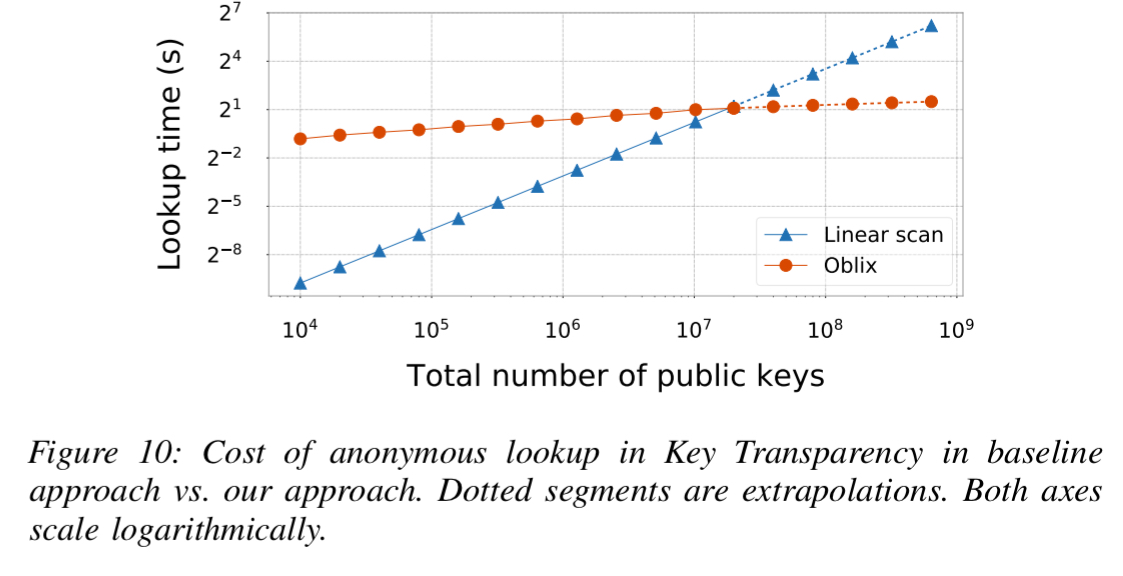
Google’s Key Transparency (KT) today does not provide anonymity – the server knows the identity of the user whose key it returns. The authors use Oblix to anonymise KT, with look-up latency 
The final case study creates an oblivious searchable encryption systems over the entire Enron email dataset (~528K emails). On average it takes 20.1ms to find the ten highest-ranking results for a keyword.