Inaudible voice commands: the long-range attack and defense

~ Adrian Colyer

Inaudible voice commands: the long-range attack and defense Roy et al., NSDI’18

Although you can’t hear them, I’m sure you heard about the inaudible ultrasound attacks on always-on voice-based systems such as Amazon Echo, Google Home, and Siri. This short video shows a ‘DolphinAttack’ in action:

[youtube https://youtu.be/21HjF4A3WE4]

To remain inaudible, the attack only works from close range (about 5ft). And it can work at up to about 10ft when partially audible. Things would get a whole lot more interesting if we could conduct inaudible attacks over a longer range. For example, getting all phones in a crowded area to start dialling your premium number, or targeting every device in an open plan office, or parking your car on the road and controlling all voice-enabled devices in the area. “Alexa, open my garage door…”. In today’s paper, Roy et al. show us how to significantly extend the range of inaudible voice command attacks. Their experiments are limited by the power of their amplifier, but succeed at up to 25ft (7.6m). Fortunately, the authors also demonstrate how we can construct software-only defences against the attacks.

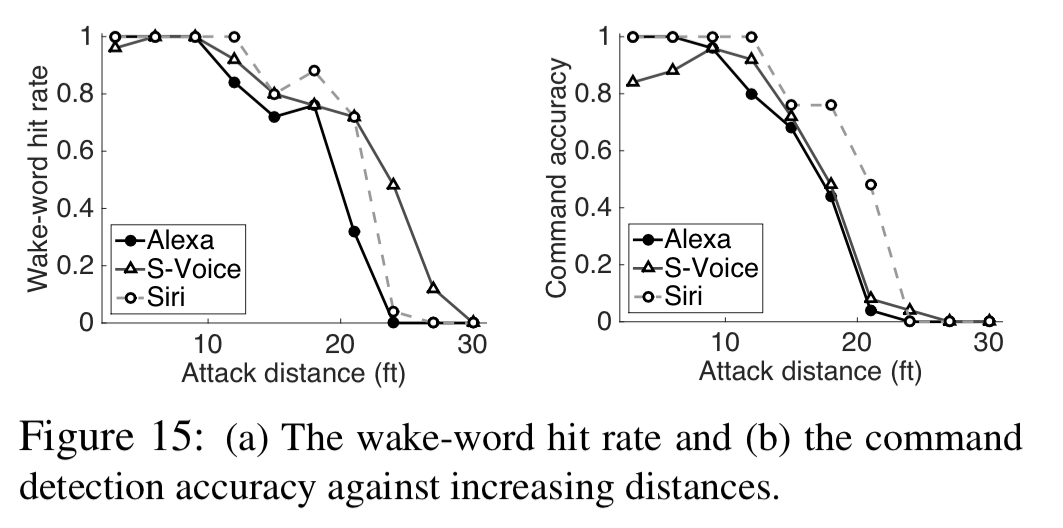
We test our attack prototype with 984 commands to Amazon Echo and 200 commands to smartphones – the attacks are launched from various distances with 130 different background noises. Figure 15 (below) shows attack success at 24ft for Amazon Echo and 30ft for smartphones at a power of 6 watt.

How microphones make the inaudible audible

Acoustic hardware such as speakers and microphones exhibit a property known as non-linearity. When signals arrive at high frequency and high enough power then they get shifted to lower frequencies.

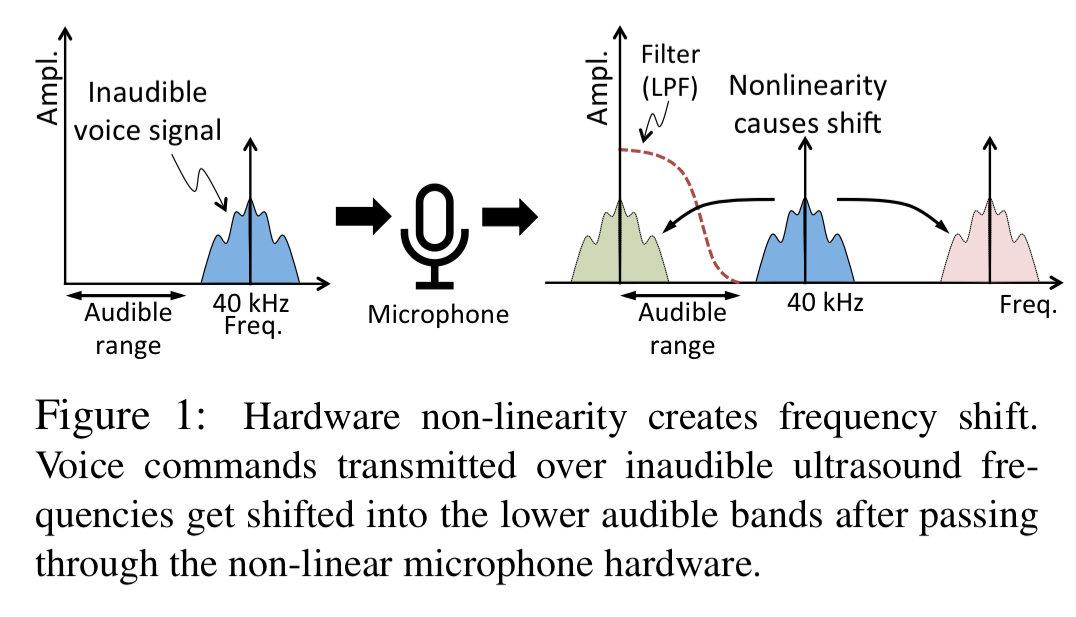
With careful signal design, the high frequency (inaudible) signal can be shifted to a lower frequency signal (within the audibility cutoff of 20kHz) within the microphone in such a way that the encoded voice command is preserved.

Start with a baseband voice signal v(t), that encodes a command such as “Alexa, mute yourself.” Now move this command to a high frequency f_{hi} = 40kHz and play it through an ultrasound speaker. At the same time, also play a constant tone at f_{hi} = 40kHz.

The combined played signal is
\displaystyle s_{hi}(t) = \cos(2 \pi f_{hi} t) + v(t)\cos(2 \pi f_{hi} t).

By the time the signal passes through the non-linear hardware and the low-pass filter (24kHz cutoff) of the microphone, what the microphone actually records is this:
\displaystyle s_{low}(t) = \frac{A_2}{2} (1 + v^2(t) + 2v(t))

(Here A is the amplifier gain).

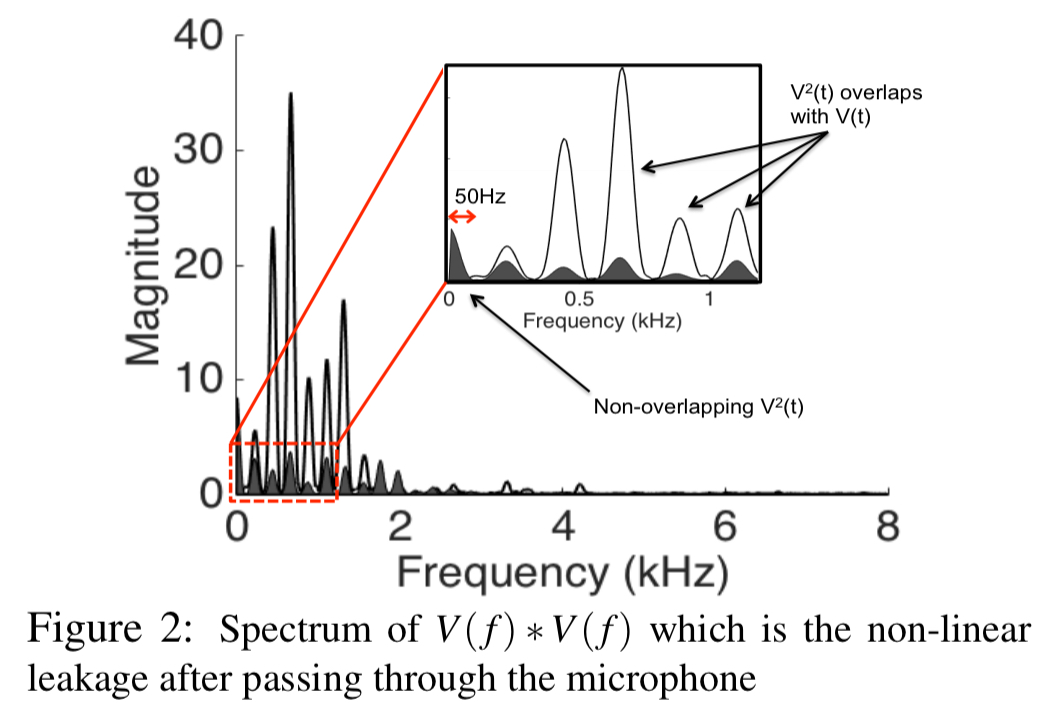
This signal contains a strong component ( A_{2}v(t) ) of the original voice signal v(t) and gets correctly decoded by almost all microphones. The relatively weak components of v^2(t) all line up underneath the voice frequencies after convolution leaving the voice signal mostly unharmed.

Trading off range and audibility

To send the high frequency signal to a target device, you have to play the sound through a speaker. Since the signal will also undergo frequency shift in the speaker, it can also become audible.

Dolphin and other attacks sidestep this problem by operating at low power, thereby forcing the output of the speaker to be almost inaudible.

Fundamentally, this is what limits the range of DolphinAttacks.

Breaking the trade-off with LipRead

So what happens if you use multiple speakers? Each at a power low enough to avoid triggering the non-linearity, but where their combined signal, as detected at the microphone, adds up to the desired attack signal.

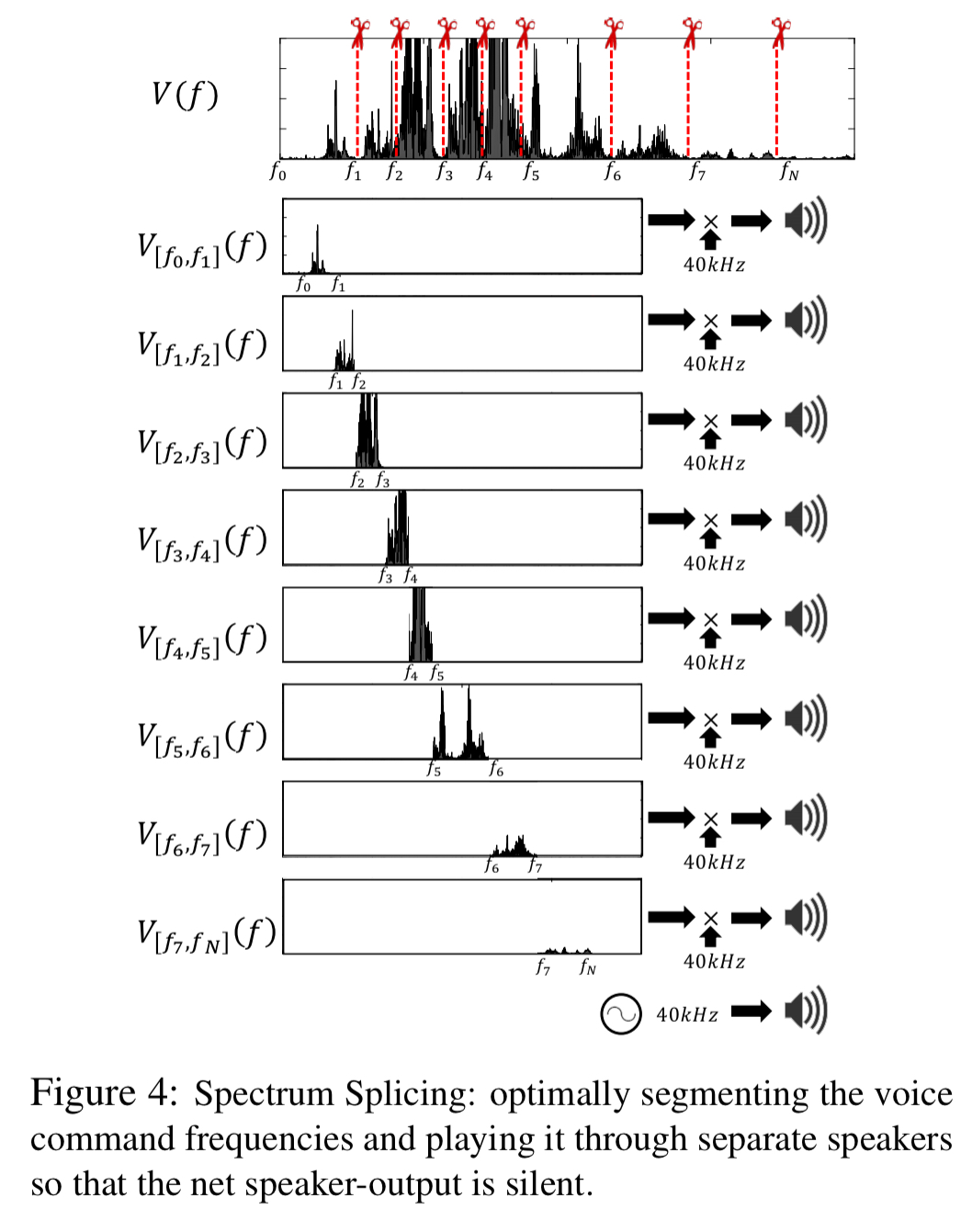
LipRead develops a new speaker design that facilitates considerably longer range attacks, while eliminating the audible leakage at the speaker. Instead of using one ultrasound speaker, LipRead uses multiple of them, physically separated in space. Then, LipRead splices the spectrum of the voice command V(f) into carefully selected segments and plays each segment on a different speaker, thereby limiting the leakage from each speaker.

Starting with the signal v(f), compute an FFT to obtain an audio spectrum V(f). We’re going to partition this into N frequency bins for N different speakers, then use an IFFT to generate the ultrasound tone for each bin.

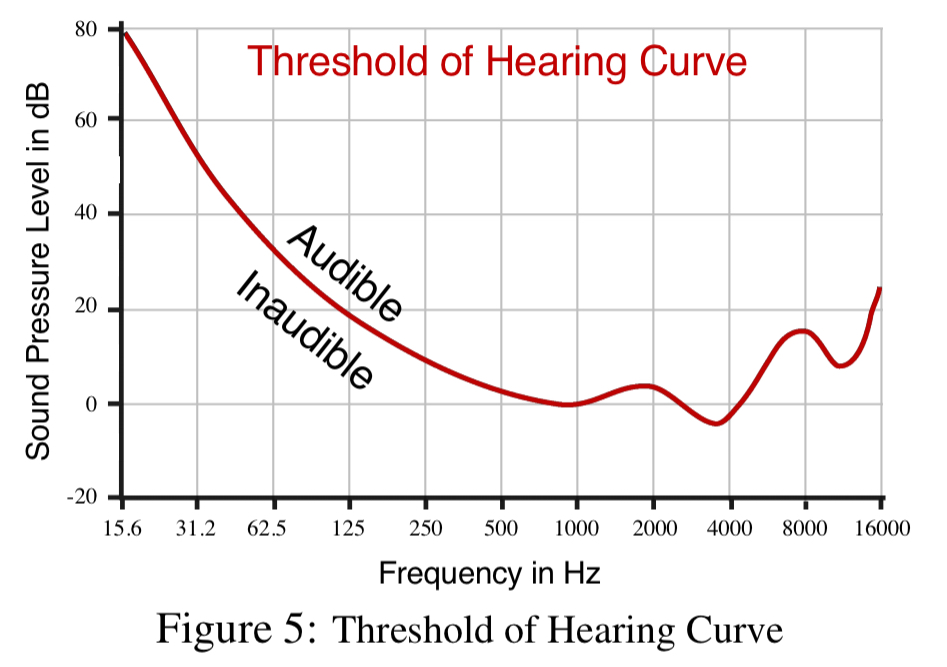
To achieve true inaudibility, we need to ensure that the total leakage is not audible. To address this challenge, we leverage the fact that humans cannot hear the sound if the intensity falls below a certain threshold, which is frequency dependent. This is known as the “Threshold of Hearing Curve.”

LipRead searches for the best partitioning of the spectrum such that the leakage is below the threshold of hearing. If multiple partitions satisfy the constraint, LipRead picks the one with the largest gap from the threshold of hearing curve.

Defences

A defence against broadcast attacks would be to use voice fingerprinting for authentication on target devices. However, the threat model considered in this paper also includes targeted attacks, and making a good enough synthesis of a user’s voice is assumed possible using known techniques.

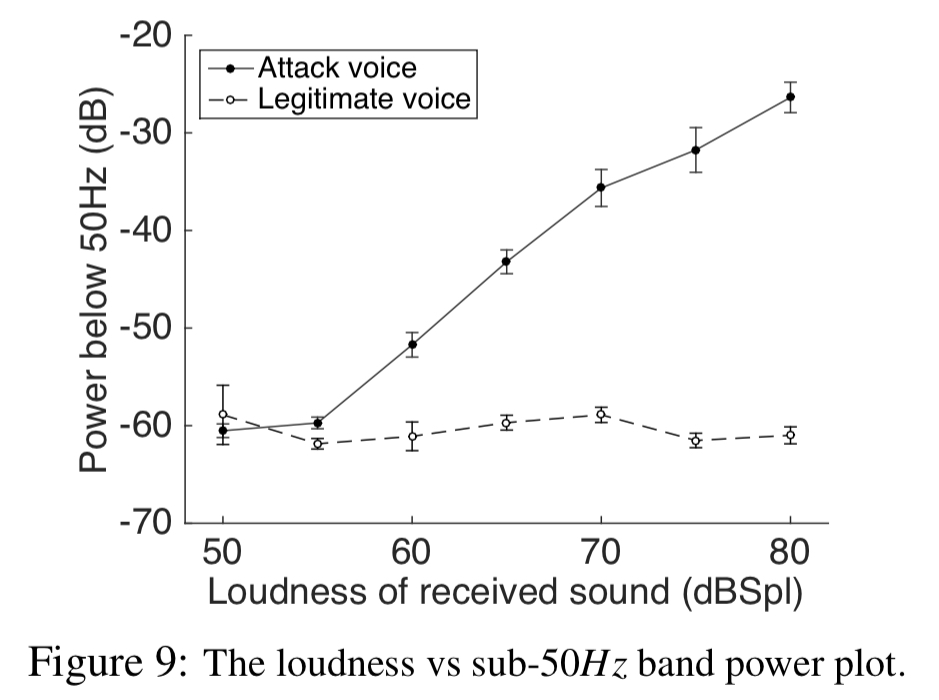
After a few dead-ends, the authors settled on a defence approach based on searching for traces of v^2(t) in the sub-50Hz spectrum.

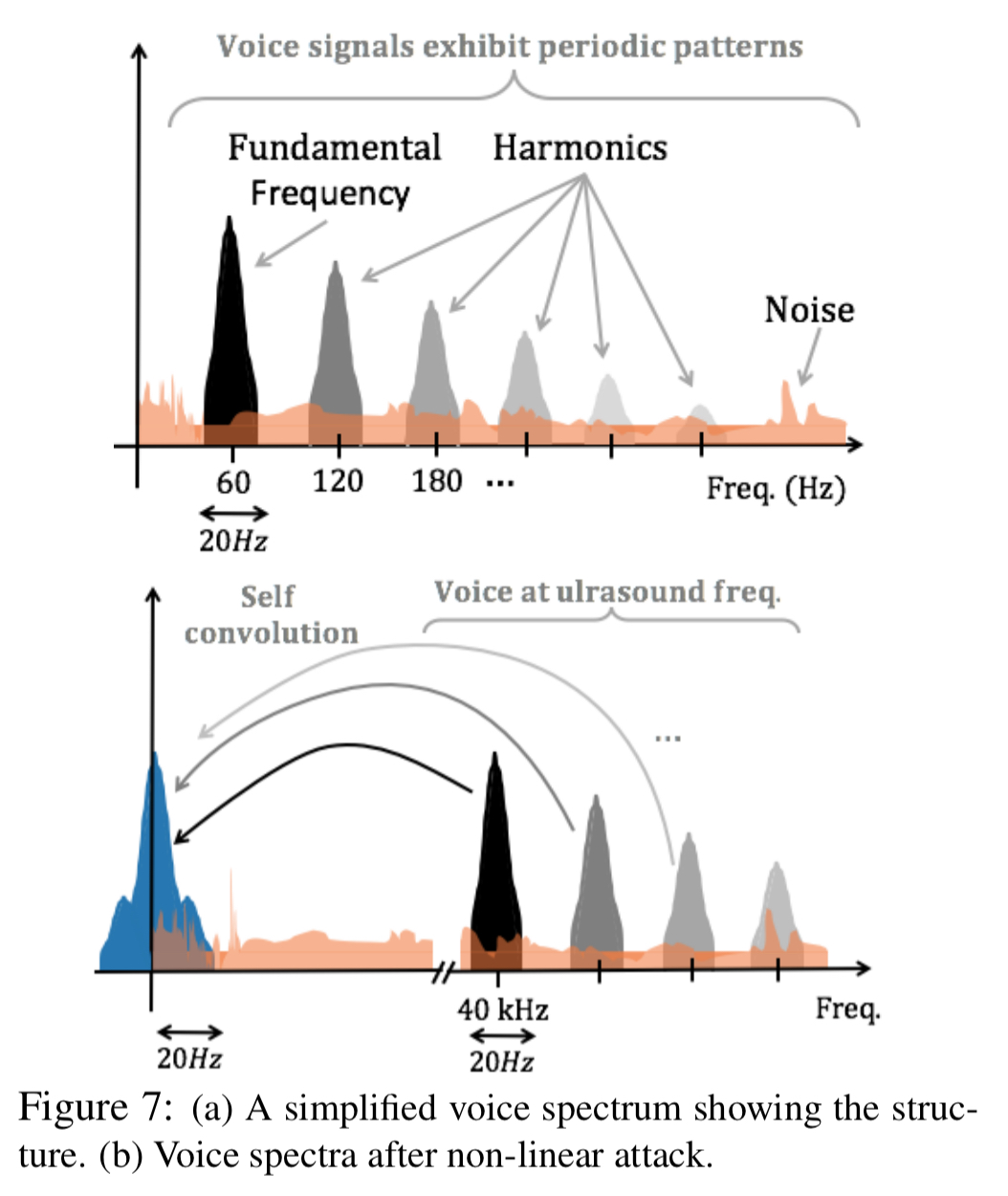
… voice signals exhibit well-understood patterns of fundamental frequencies, added to multiple higher-order harmonics. We expect this structure to partly reflect in the sub-50Hz band of s(t) (that contains v^2(t) ), and hence correlate with carefully extracted spectrum above 50Hz (which contains the dominant v(t) ). With appropriate signal scrubbing, we expect the correlation to emerge reliably, however, if the attacker attempts to disrupt correlation by injecting sub-50Hz noise, the stronger energy in this low band should give away the attack. We intend to force the attacker into a zero sum game.

There are three features used to detect an attack. Firstly, power in sub-50Hz:

The second feature is a correlation coefficient looking at correlations between power variations in the sub 20Hz band and the fundamental frequency:

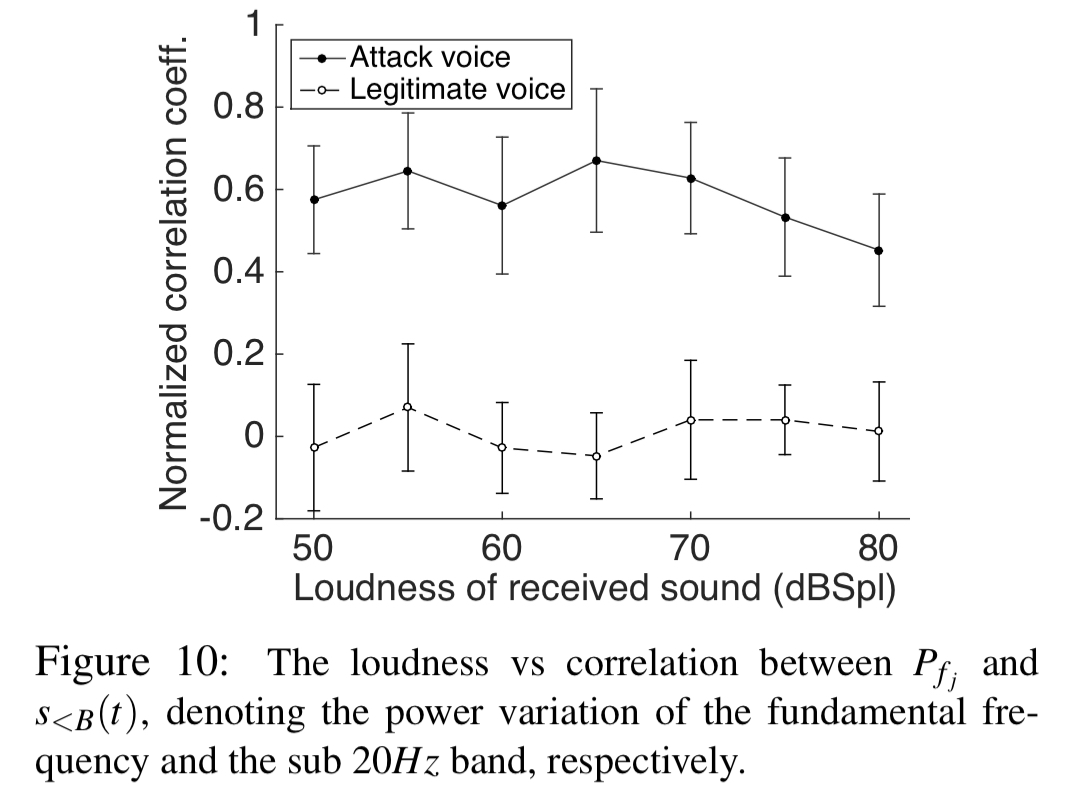
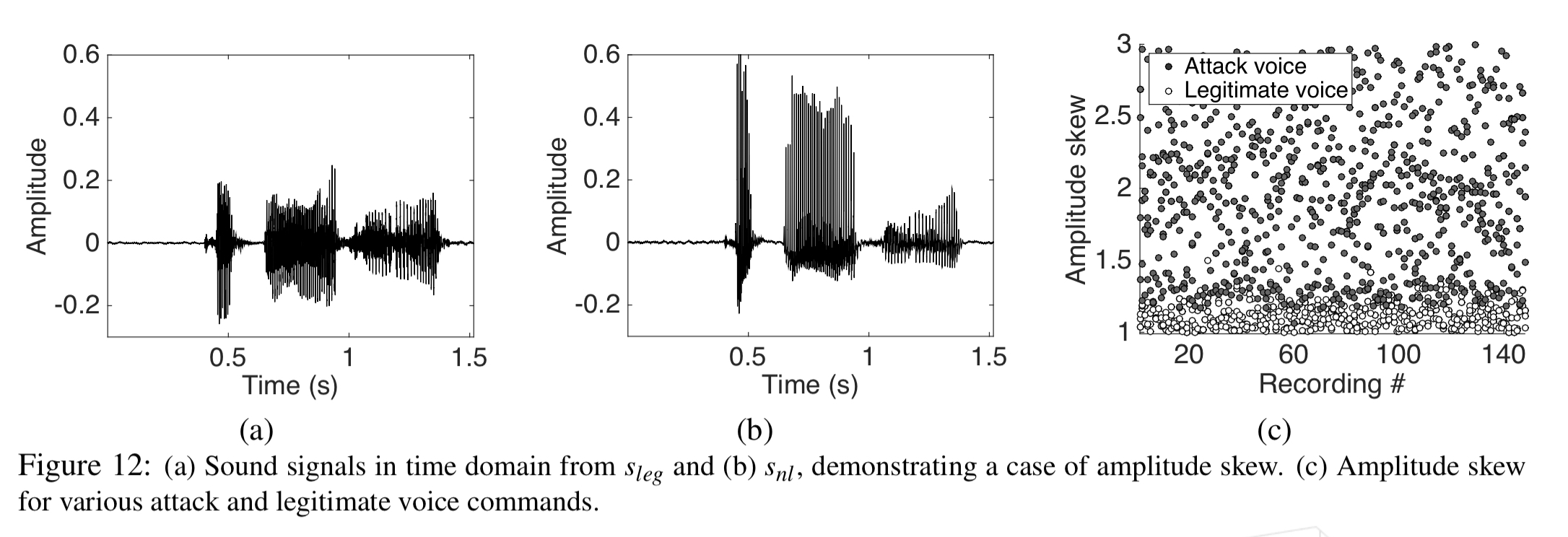
The final feature detects amplitude skew. Legitimate voice signals have well balanced positive and negative harmonics (a), but the signal v^2(t) has only positive amplitude. This biases the overall result on the positive side (b).

Experimental results

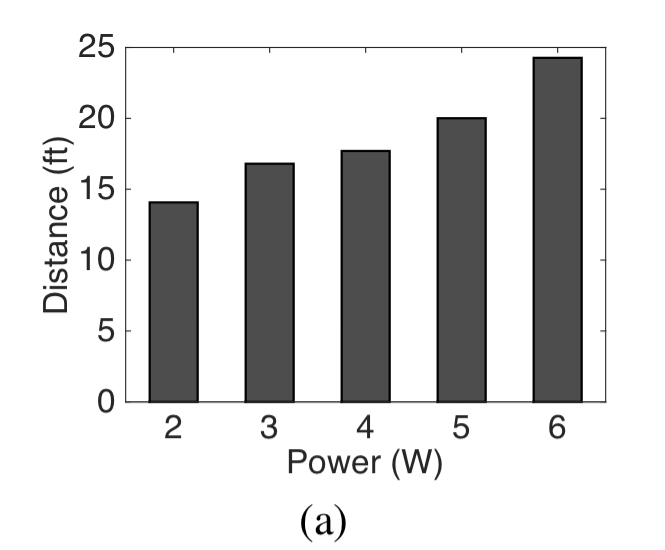
The chart below shows the achieved attack range when targeting an Echo device, for given power. “More powerful amplifiers would certainly enhance the attack range, however, for the purposes of prototyping we designed our hardware in the lower power regime.”

Next up lets take a look at the effectiveness of slicing. With no partitions, the signal is clearly audible, and by six partitions with optimal partitioning it is almost totally inaudible:

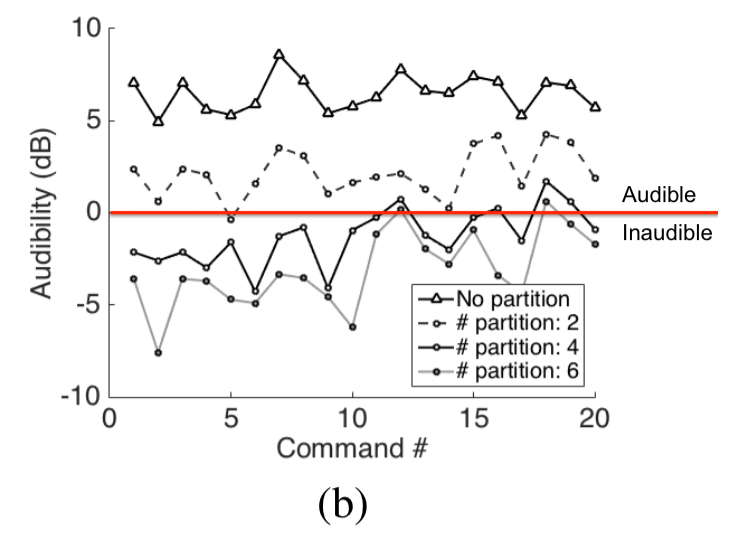
With 60 speakers in our array, we use 6 segments, each played through 5 speakers; the remaining 31 were used for the second \cos(2 \pi f_c t) signal. Note that the graph plots the minimum gap between the hearing threshold and the audio playback, implying that this is a conservative worst case analysis.

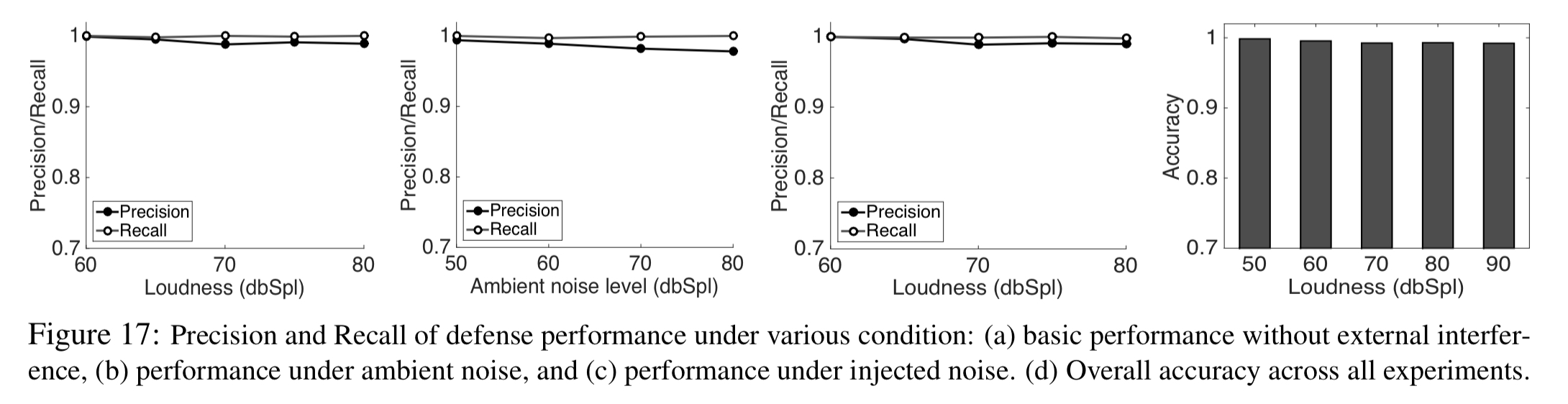
The defence technique has excellent precision and recall even in noisy environments, or when an attacker deliberately tries to circumvent it: