Programming and proving with distributed protocols

Programming and proving with distributed protocols Sergey et al., POPL 18

Last week we looked at the verification of Rust’s type-based safety guarantees, and a verification toolchain for proving properties of JavaScript programs. Today it’s the turn of Disel, a framework for developing and verifying message-passing based distributed systems (it would seem to fit beautifully with distributed actor-based systems). Disel has two very interesting and important properties:

It uses dependent types to verify program correctness with respect to a specific abstract protocol: any well-typed program is correct. Contrast this with the more traditional process of refinement which involves demonstrating that a lower-level implementation correctly refines a more abstract one.
It supports compositional verification: modules may be independently verified and subsequently composed without needing to re-verify all existing code.

Disel is a verification framework incorporating ideas from dependent type theory, interactive theorem proving, separation-style program logics for concurrency, resource reasoning, and distributed protocol design.

For protocol designers, Disel provides a DSL for defining protocols in terms of state-space invariants and atomic primitives. The primitives define transitions synchronising message-passing with changes to the state of a local node.
For system implementors, Disel provides a higher-order programming language with a complete toolset of programming abstractions, in conjunction with low-level primitives for message-passing distributed communication.

Disel’s dependent type system makes programs protocol-aware and ensures that well-typed programs don’t do wrong…

For human verifiers, Disel provides an expressive higher-order separation-style program logic that allows programs to be assigned declarative Hoare-style specifications, which can be subsequently verified in an interactive proof mode.

The whole thing is implemented on top of the Coq proof assistant, using Coq’s dependent types and higher-order programming features. Programs written in Disel can be extracted to OCaml, making use of a small (250 loc) trusted shim implementation, and hence run on multiple physical nodes. Disel is available in GitHub at https://github.com/DistributedComponents/disel, along with proofs of all of the examples from the paper.

Specifying protocols in Disel

A protocol in Disel provides a high-level interface between distributed system components… Disel protocols serve to separate concerns: implementations can refine details not specified by the protocol, invariants of the protocol can be proven separately, and interactions between components in a larger system can be reasoned about in terms of their protocols rather than their implementations.

Protocols are defined as state transition systems with send and receive transitions. For a simple distributed calculator protocol that permits a client to send a compute request with some argument arg, and a server to respond with f(arg), the send and receive transitions might look like this:

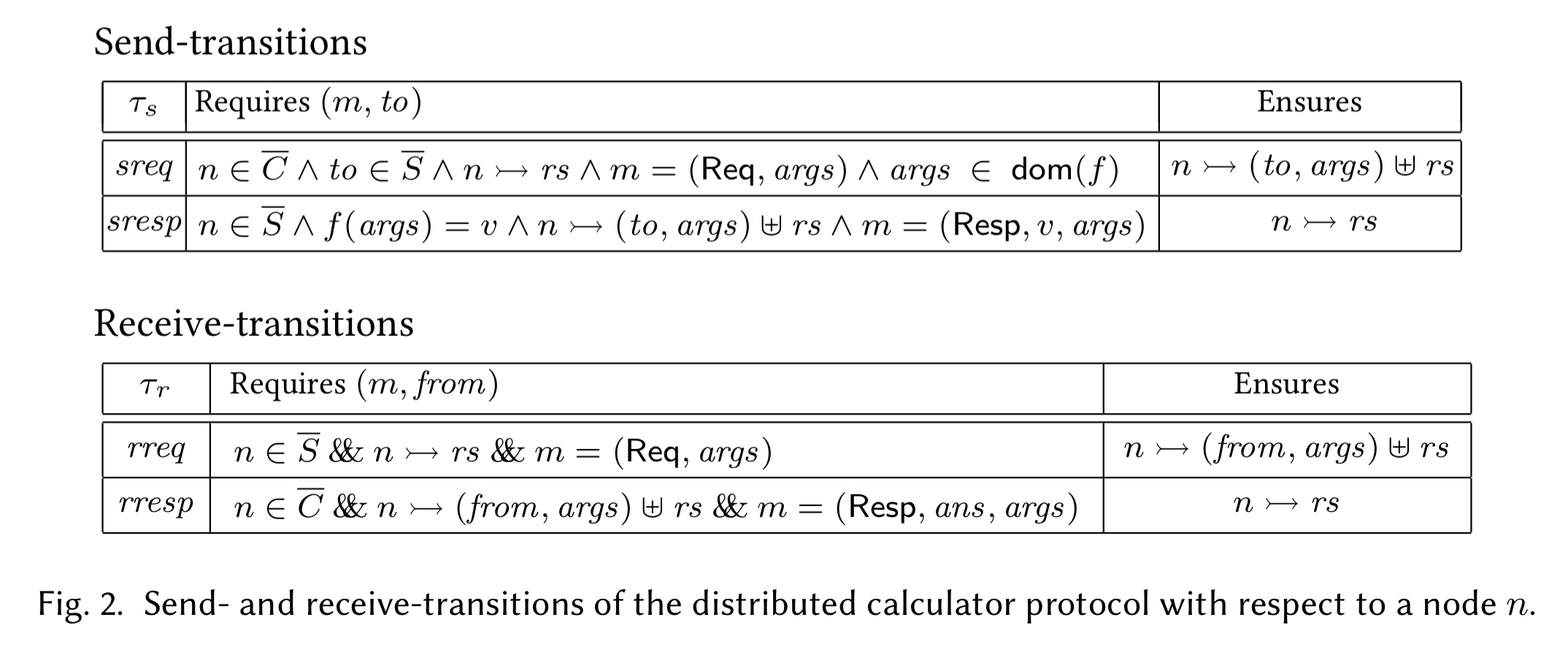
The first column is the transition name, the second column specifies the preconditions, and the last column specifies the post-conditions. A message sent to a node only triggers the corresponding receive transition if the state of that node, along with the message, satisfies the transition’s precondition.

Implementing protocols with Disel

Disel provides a library of transition wrappers, such as the generic send wrapper which takes a send transition of a protocol and yields a program that sends a message. Wrapped transitions have Hoare types (specifications) – a fancy way of saying they have pre- and post-conditions:

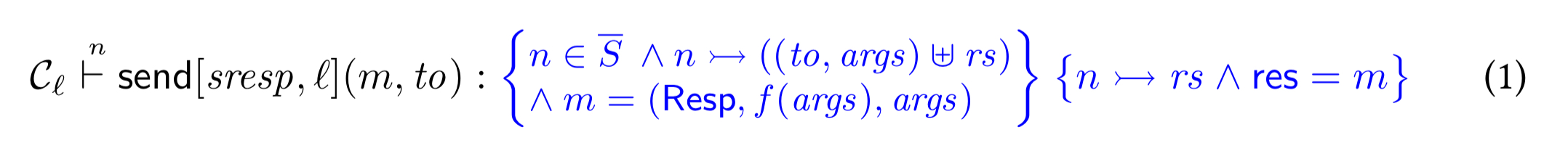
Receive wrappers match messages taken from the message soup, which models both the current state and history of the network. Messages in Disel are never ‘thrown away’, instead they are added to the soup where they remain active until received, at which point they become consumed.

A blocking receive for calculator request messages might look like this:

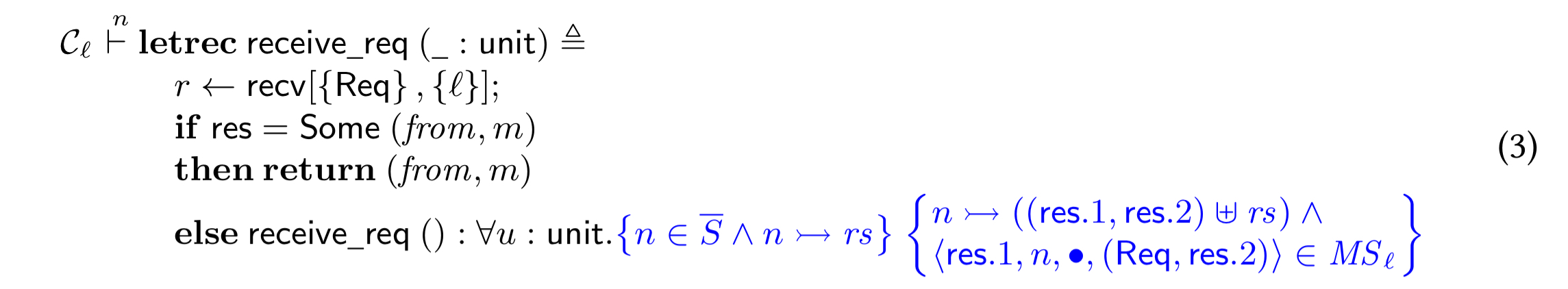
In actual code, it’s more like this (this fragment is taken from a different example, implementing a receive transition in a 2PC coordinator):

We can use the blocking receive building block to make a simple server:

Inductive invariants

We’d like to assign a type to the simple server specified above (remember that in Disel, guarantees come through the dependent type system). However, we run into a problem with the use of the partial function $f$ — the function that the calculator service computes over the passed argument.

Since $f$ is partially defined, Disel will emit a verification condition (VC), requiring us to prove that $f$ is defined at $args$ . Unfortunately, the postcondition in the spec of receive_req does not allow us to proved the triple: we can only conclude that a message from the soup is consumed, but not that its contents are well-formed, i.e., that $args \in dom(f)$ .

The property that we want to prove though, is an inductive invariant with respect to the transitions in the calculator protocol: if it holds in some initial state $s_0$ , then it holds for any state $s$ reachable via transitions from $s_0$ . Since every well-typed program in Disel is composed of protocol transitions, it will automatically preserve the inductive invariant as long as the pre-state satisfies it.

To account for this possibility of invariant elaboration, Disel provides a protocol combinator, WithInv that takes a protocol $\mathcal{P}$ and a state invariant $\mathcal{I}$ , proven to be inductive wrt. $\mathcal{P}$ , and returns a new protocol $\mathcal{P}'$ , whose state-space definition is strengthened with $\mathcal{I}$ . That is, the pre/postcondition of every transition can be strengthened with $\mathcal{I}$ “for free” once $\mathcal{I}$ is shown to be an inductive invariant.

Combining protocols

Disel permits applications to participate in multiple protocols by providing an injection/protocol framing mechanism — separation logic is everywhere at the moment it seems — inspired by the FCSL program logic of Nanevksi et al..

Running Disel programs

Disel combines two traits that rarely occur in a single tool for reasoning about programs. First, thanks to the representation of Hoare types by means of Coq’s dependent types, the soundness result of Disel scales not just to a toy core calculus, but to the entirety of Gallina, the programming language of Coq, enhanced with general recursion and message-passing primitives. Second, Disel programs are immediately executable by means of extracting them into OCaml, which provides the features that Gallina lacks: general fixpoints, mutable state, and networking constructs, enabled by our trusted shim implementation.

To run an extracted Disel program you need to supply a set of nodes, and assign each node a program to run, together with an initial distributed configuration satisfying all imposed state-space invariants. Disel’s type-safety guarantees apply in a distributed setting, and thus well-typed programs are not affected by the execution of programs running concurrently on other nodes. Such programs are always safe to run when their precondition is stable and satisfied. (Liveness is part of future work).

Disel’s distributed separation logic

Section 3 of the paper runs to about 7 pages, describing the formal model of state and protocols in Disel. I’m going to reduce that down to just a few paragraphs here, so if you’re interested in learning more you’ll find a whole lot more detail in the paper itself, as well as a worked example of implementing a 2PC protocol.

There’s a bunch of state that defines the message soup and per-node local state, and the notion of a world, which combines protocols and client-provided send-hooks. Send hooks are used when composing protocols, and permit the specification of additional preconditions on message sends.

The programming language of Disel is embedded in Coq, and offers the following commands:

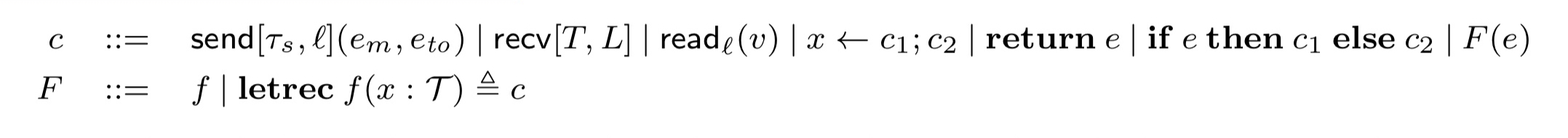
There is the obligatory set of logic judgements and inference rules including the frame rule for horizontal composition of protocols, and a non-deterministic small-step operational semantics. It is the combination of WithInv and Frame which enables modular invariant proofs and distributed systems composition.

We believe… that compositionality, afforded by Disel’s logical mechanisms, is a key to make the results of future verification efforts reusable for building even larger verified distributed systems.

Implementation experience

The following table summarise the proof effort (in terms of LOC) and build times for the calculator example and a 2PC protocol implementation.

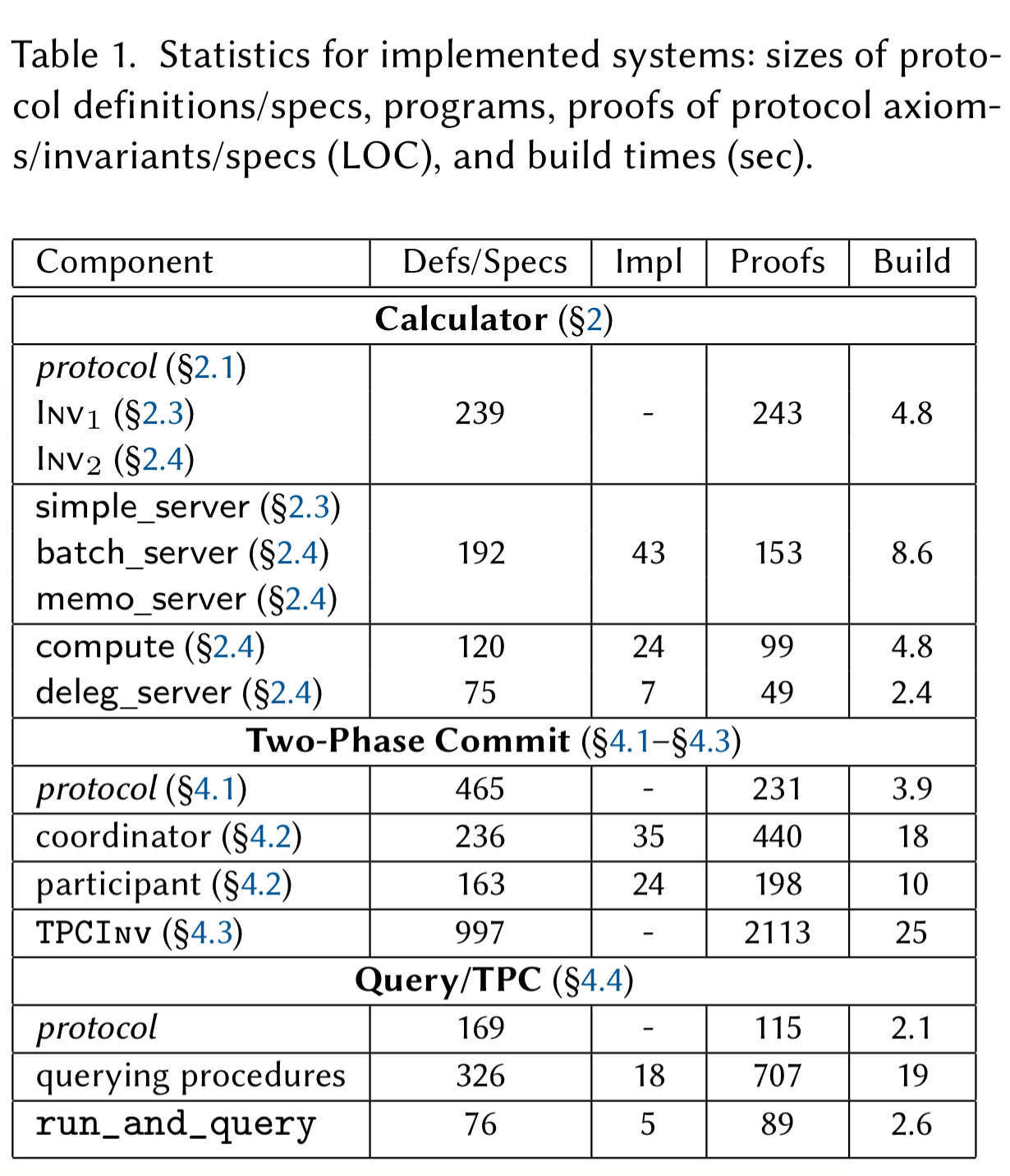
… safety proofs of interesting systems can be obtained in a reasonably short period of time and with moderate verification effort (e.g., the full development of the core 2PC system took nine person-days of work). Given that the current version of Disel employs no advanced proof automation, beyond what is offered by Coq/Ssreflect, for discharging program-level verification conditions or inductive invariant proofs, we consider these results encouraging for future development.

the morning paper

a random walk through Computer Science research, by Adrian Colyer
Made delightfully fast by strattic