Seeing is believing: a client-centric specification of database isolation

~ Adrian Colyer

Seeing is believing: a client-centric specification of database isolation Crooks et al., PODC’17

This paper takes a fresh look at the issue of isolation levels, a topic we’ve looked at before and which contains quite a bit of complexity. The gold standard reference for understanding isolation is Adya’s Generalized isolation level definitions. Unlike the definitions that went before, Adya strove to give portable isolation level definitions that were not based on a given implementation technique. Adya defines isolation levels according to properties of directed serialisation graphs constructed over execution histories. If you’re actually trying to build an application (i.e., use a database), Crooks et al. argue that these graphs aren’t the most natural way to think about what’s going one.

From a programmer’s perspective, isolation guarantees are contracts between the storage systems and their clients, specifying the set of behaviours that clients can expect to observe – i.e., the set of admissible values that each read is allowed to return. When it comes to formally defining these guarantees, however, the current practice is to focus, rather than on the values that the clients can observe, on the mechanisms that can produce those values – i.e., histories capturing the relative ordering of low-level read and write operations.

So the authors set out to build a new model expressing isolation guarantees as properties of state that applications can observe. However you come at it, there are of course going to be some similarities – Adya’s phenomena I find in many cases to be quite succinct expressions of states I may observe, and the sequence of states Crooks et al. want us to reason about have a certain graph-like structure if you squint just right. In fact, selecting Adya’s model as baseline, the authors prove that their definitions are equivalent to his. The state based model turns out to have some nice properties:

  • It makes clear to developers what anomalies (if any) their application can expect to observe, “thus bridging the semantic gap between how isolation is experienced and how it is formalized.”
  • It makes it easier to compare guarantees from distinct but semantically close isolation guarantees, since any distorting effects of implementation artefacts are removed.
  • Based on this, the authors show that several isolation levels previously thought to be distinct, are, from the clients’ perspective, actually equivalent!
  • Finally, the viewing parallel snapshot isolation through the state-based lens revealed an opportunity to avoid the slowdown cascades which have inhibited the adoption of stronger isolation models in larger datacenter settings.

Ultimately, the insights offered by state-based definitions enable us to organize in a clean hierarchy what used to be incomparable flavours of snapshot isolation.

A state-based model

Let a storage system state s be a mapping from a set of keys \mathcal{K} to a set of values \mathcal{V}. Initially the system starts out with every key mapped to the special undefined value, \bot

A transaction T is an ordered set of read and write operations. A read operation r(k,v) retrieves the values v by reading key k. A write operation w(k,v) updates k to the new value v.

If we start with the system in some state s_p (called the parent state of a transaction) and apply a transaction T, we end up with a new state in which the only differences are that the writes from T have been applied. (For simplicity, a transaction is assumed to write a key only once). In the notation developed in the paper, this is written as s_p \xrightarrow{T} s'. A series of zero or more such state transitions from an initial starting state s is written s \xrightarrow{*} s'.

So far so good. Now we need to grapple with the concept of an execution. Given a set of transactions, \mathcal{T}, an execution e is the sequence of states \mathcal{S}_e that the system passes through (starting from the initial state) when applying the transactions in \mathcal{T} in some order. So one execution might be “we start out in the initial state and then apply T_a, T_b, and T_c in that order,” and other execution for the same transaction set might be “we start out in the initial state and then apply T_b, T_c, T_a in that order.”

Here’s the subtle thing it took me a few readings to fully grasp. Take the order T_a, T_b, T_c again for a moment. There is no requirement that the state a given transaction sees be the immediately preceding state in the execution. So for T_c it could be seeing the initial state, the state after applying T_a, or the state after applying T_a and T_b. Since a read operation r(k,v) is defined in terms of the value v that is seen in response to a read of the key k we do have some constraints: the value v returned from the read must be compatible with the value of v in the state from which the operation reads. The subset of states in the execution for which this condition holds are called the read states. To put it another way, the read states of an operation are all of the states it could possibly have read from given the value that it actually observed.

We need a picture! Take four transactions with read and write operations as follows:

  • T_a : w_1(x, x_1)
  • T_b: r_2(y, y_1), r_3(z, z_0)
  • T_c: w_2(y, y_1)
  • T_d: w_3(y, y_2), w_4(z, z_1)

We start out in the initial state, s_0.

For this execution, we’ll say that T_a is applied first. Since it can only read from the initial state, we inevitably end up with:


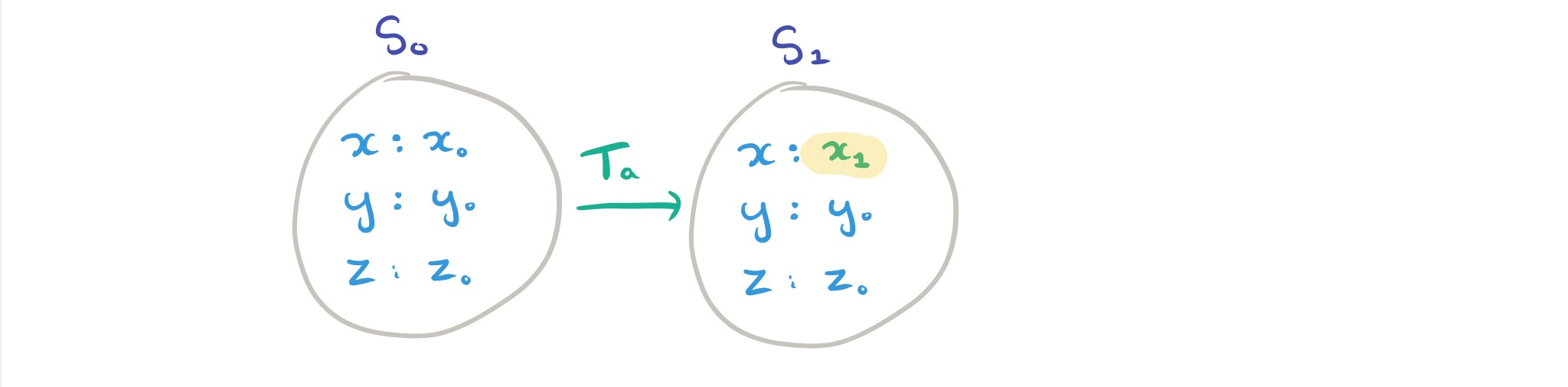
T_c goes next, taking us to state s_2:

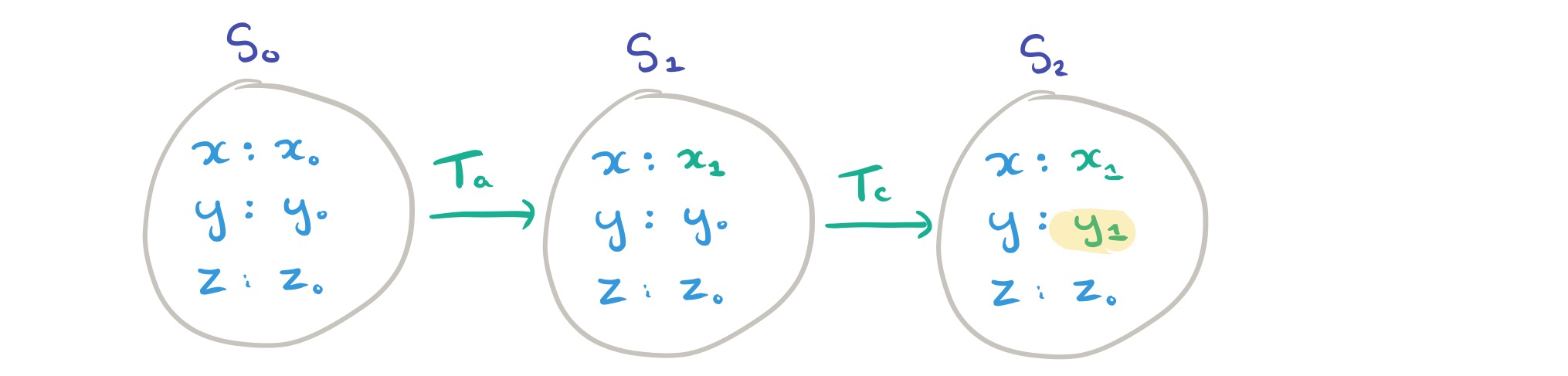
and then it’s the turn of T_d:

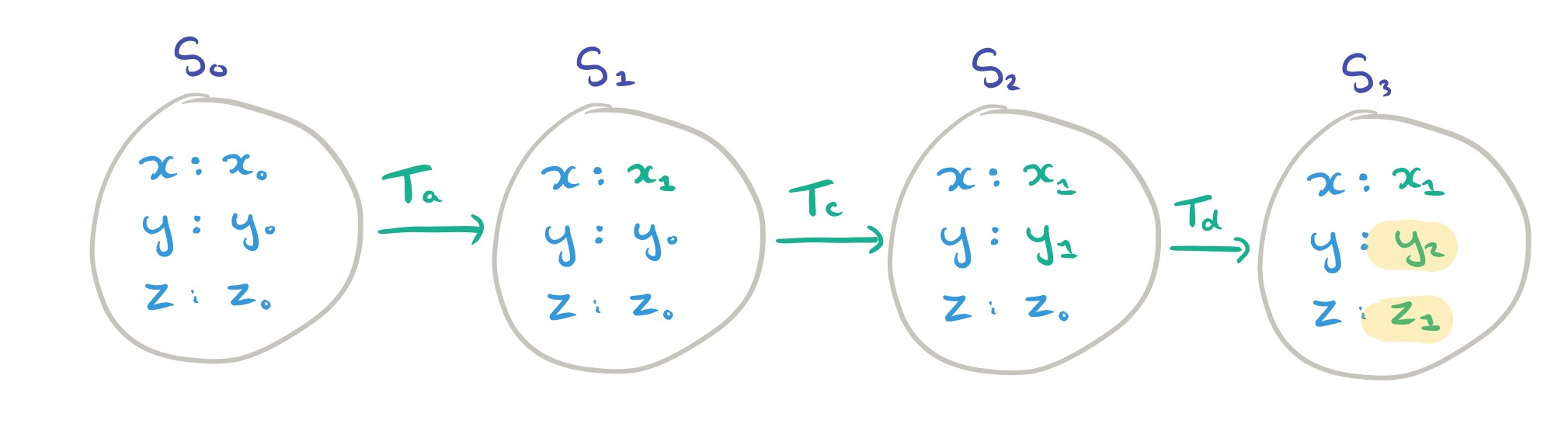
(Note that these first three transactions handily didn’t include any read operations!). Next up in the execution is T_b. This does contain read operations, two of them. Operation r_2 reads key y and sees y_1. The only possible read state for r_2 therefore is s_2.

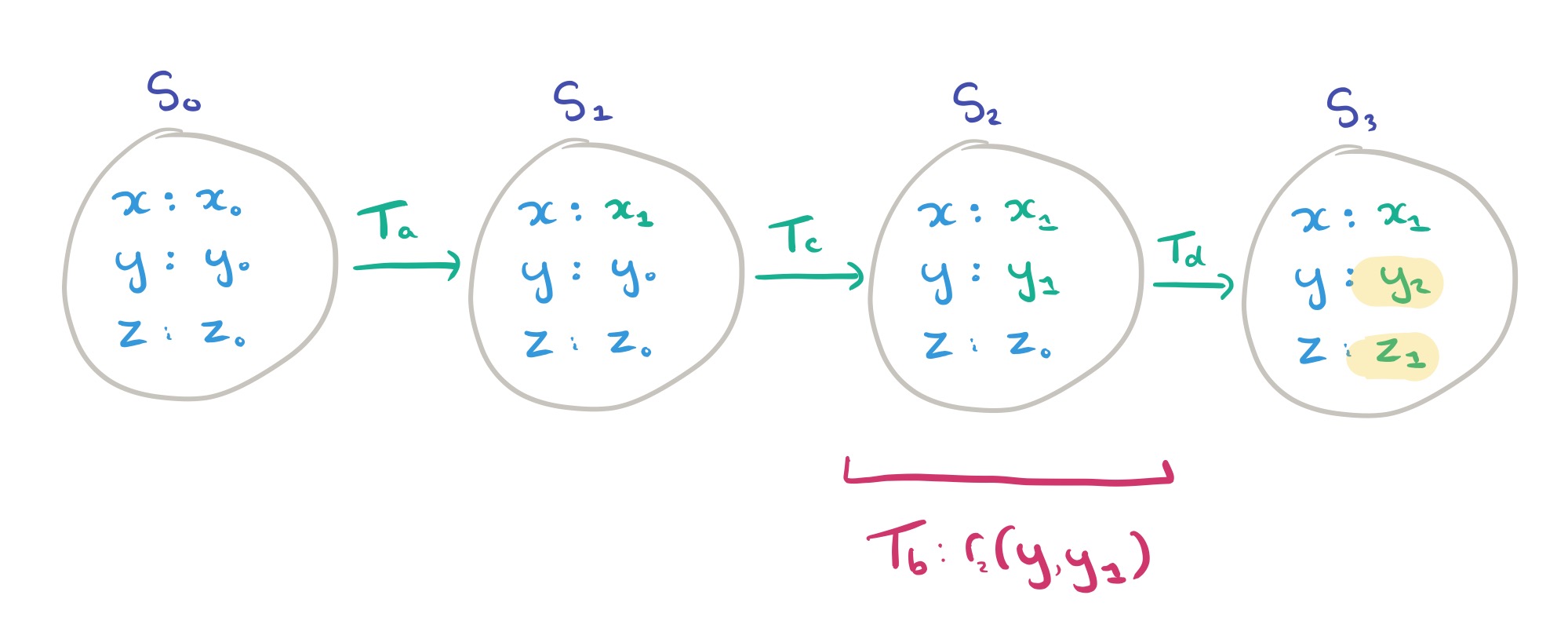
Operation r_3 reads key z and sees value z_0. The possible read states for this operation (states in which z has value z_0) are therefore:

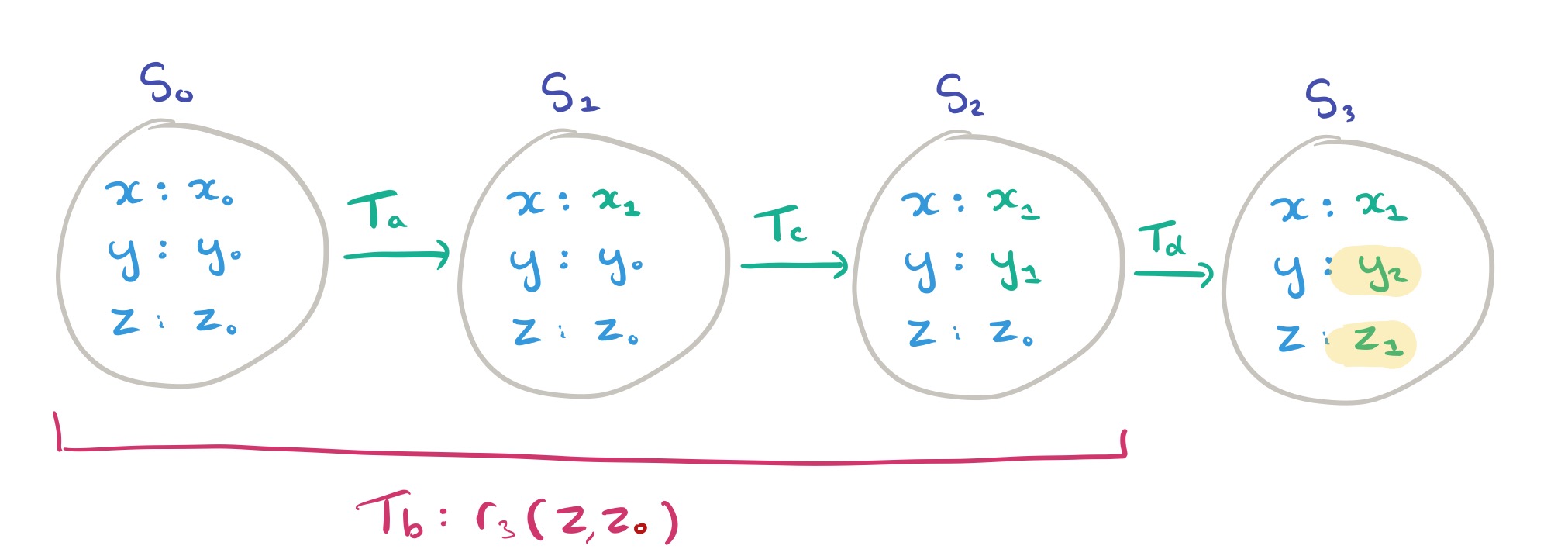
The read precondition predicate, PREREAD, holds for a transaction if all the read operations in the transaction have a non-empty read set. That is, every read seen by the transaction was at least possible according to our rules so far! In the example above, ~PREREAD(T_b) holds since the read set is non-empty for both reads. The PREREAD predicate holds for an entire execution if it holds for every transaction in the execution.

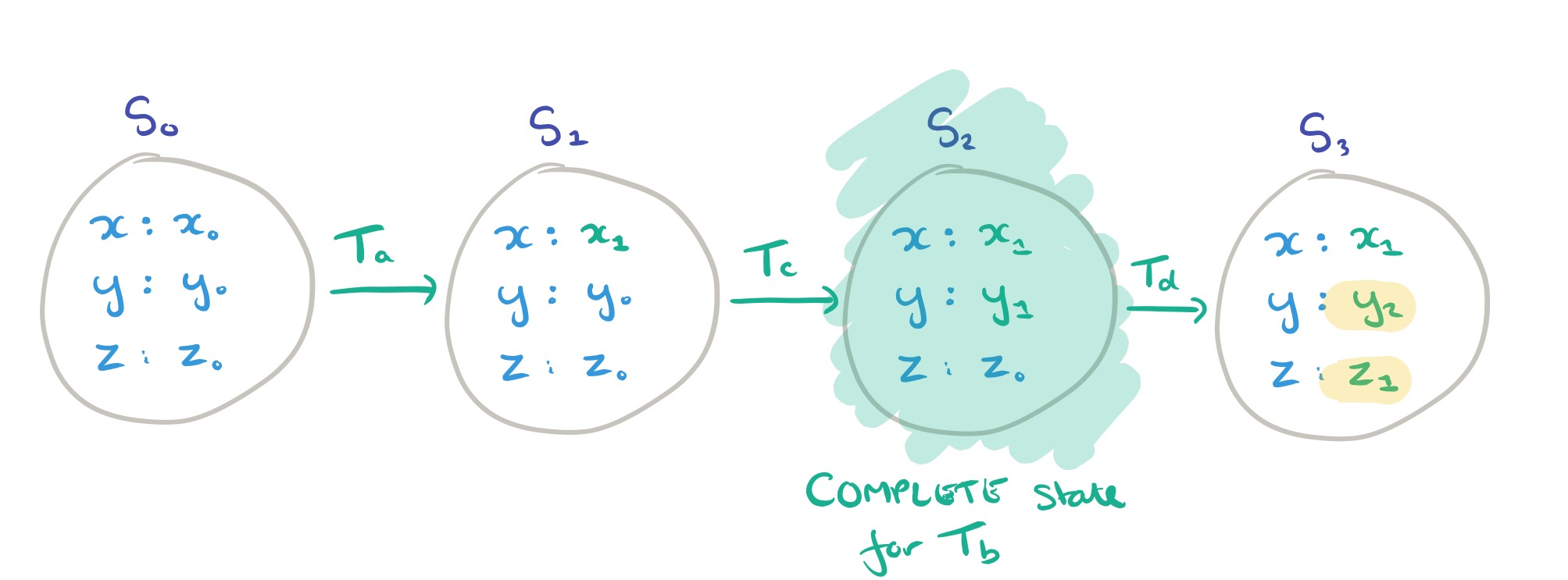
For a given transaction T, a state s in an execution e is said to be complete if every operation in T can read from s (i.e., s is in the read set of every operation in T). We denote this as COMPLETE_{e,T}(s). In our running example, the only complete state for transaction T_b is s_2. There is no guarantee that a complete state will exist for any given transaction.

Expressing isolation guarantees in the state-based model

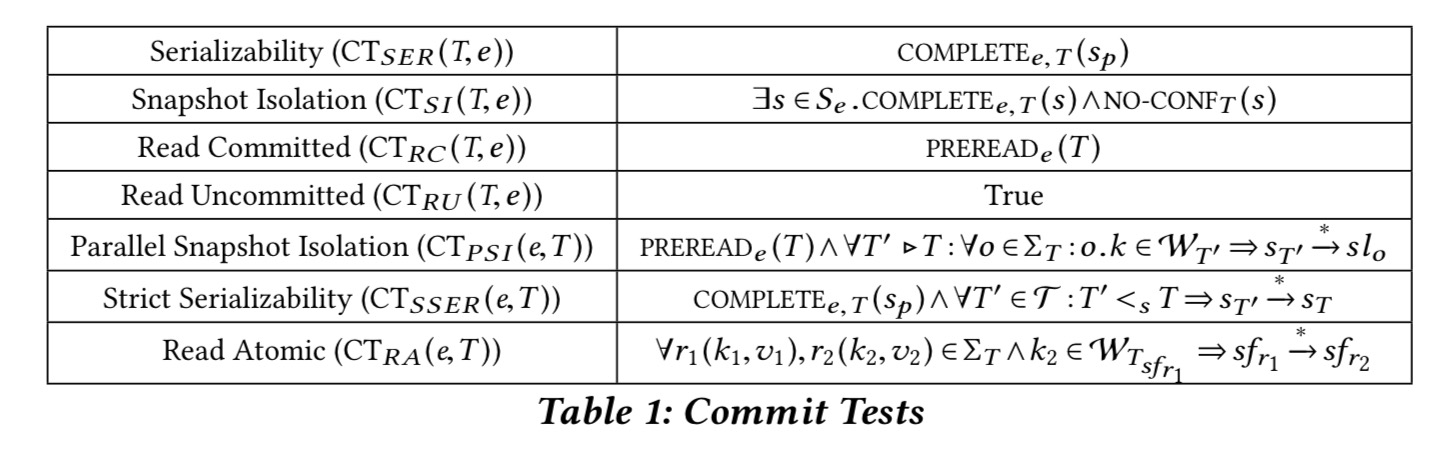
OK! That was a lot of definitions, but now it’s payback time. Given our state-based model, we can use it to express isolation models as constraints on permissible read states for read operations, and parent states for transactions. The set of constraints that define an isolation guarantee are called its commit tests.

Let’s start with a simple one: serializability.

Serializability requires the values observed by the operations in each transaction T to be consistent with those that would have been observed in a sequential execution.

That turns into two commit test obligations:

  1. Every operation in T must read from the same state (i.e., a state that is complete for T).
  2. This complete state must also be the parent state for T (i.e., the state that T transitions from).

If we want strict serializability we need to add one more commit test condition. We say that transaction T_1 precedes T_2 if the commit time of T_1 is less than the start time of T_2 (i.e, T_1 commits before T_2 starts). The extra condition is this: if T_1 precedes T_2 then T_1 comes before T_2 in the execution.

What about read committed? We know this is weaker that serializability, but how exactly?

Read committed allows T to see the effects of concurrent transactions, as long as they are committed. The commit test therefore no longer constrains all operations in T to read from the same state; instead it only requires each of them to read from a state that precedes T in the execution e.

The commit test for read committed is simply PREREAD!

(In read uncommitted btw. pretty much anything goes, and the commit test adds no further constraints over the base model).

Snapshot isolation is like serializability, but drops the commit test requirement that the complete state a transaction reads from be its parent state. Other transactions may commit in-between, so long as the effects of those transactions are not observed. This leads to two commit test conditions:

  • Every operation in T must read from the same state (i.e., a state that is complete for T). This is the same condition as we had for serializable.
  • T cannot modify (write) any keys that changed value between the complete state that T reads from, and the actual parent state of T.

Going back to our example, s_2 is a complete state for T_b. Under snapshot isolation we would be allowed to extend our execution with T_b following (having as its parent state) s_3, but under serializability we would not.

Here’s a summary table of the commit tests we’ve looked at so far, and a couple that we haven’t discussed yet:

Parallel snapshot isolation (PSI) was recently proposed by Sovran et al to address SI’s scalability issues in geo-replicated settings. Snapshot isolation requires transactions to read from a snapshot (a complete state in our parlance) that reflects a single commit ordering of transactions. The coordination implied by this requirement is expensive to carry out in a geo-replicated system and must be enforced even when transactions do not conflict. PSI aims to offer a scalable alternative by allowing distinct geo-replicated sites to commit transactions in different orders.

The client-centric definition of PSI makes it clear that operations do not necessarily observe a complete state. See section 4 in the paper for full details and for the read atomic discussion.

A fresh perspective on isolation levels

By cleanly separating high-level properties from low-level implementation details, a state-based model makes the plethora of isolation guarantees introduced in recent years easier to compare. We leverage this newfound clarity … to systematize snapshot-based guarantees.

The client perspective shows that snapshot-based guarantees differ on three dimensions: time (logical or real); snapshot recency; and state completeness. The result is a hierarchy that looks like this:

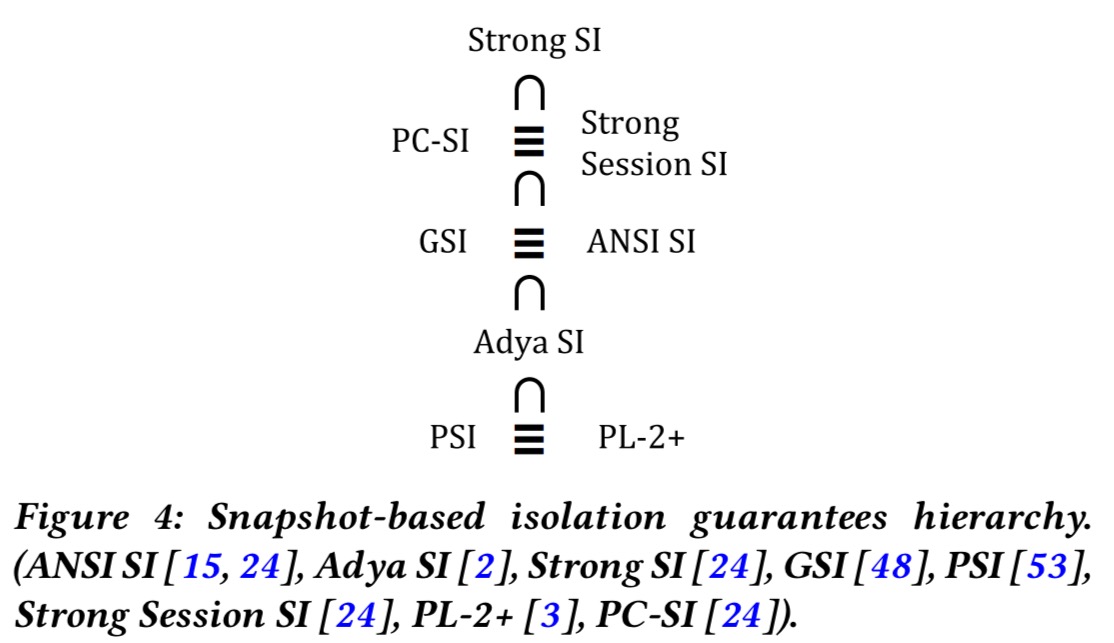
As you move from the top to the bottom of the hierarchy, implementation scalability improves, as can be seen in the reducing commit test conditions below. See section 5.2 in the paper for a good discussion on this, which space precludes me from covering here.

Using the insights gained from focusing only on observable differences to clients, the authors realised that the history-based definition of PSI requiring a total commit order across all transactions in a datacenter, even across different keys, was overly restrictive. The ‘true’ dependencies need only be those observable to the application (causal?). The authors tested the potential performance improvements this could realise using the TARDiS key-value store:

On a workload consisting of read-write transactions (three reads, three writes) accessing data uniformly over 10,000 objects, we found that a client-centric approach decreased dependencies, per transaction, by two orders of magnitude (175x), a reduction that can yield significant dividends in terms of scalability and robustness.

Details are in section 5.3.