Adaptive logging: optimizing logging and recovery costs in distributed in-memory databases

~ Adrian Colyer

Adaptive Logging: Optimizing logging and recovery costs in distributed In-memory databases Yao et al., SIGMOD 2016

This is a paper about the trade-offs between transaction throughput and database recovery time. Intuitively for example, you can do a little more work on each transaction (lowering throughput) in order to reduce the time it takes to recover in the event of failure. Recovery is based on information in logs, classically an ARIES-style write-ahead log, that records the values of data items.

In the case of in-memory databases, you can also go the other way, and do a little less work when creating the logs (recording information for use in recovery) at the expense of longer recovery times, but gaining higher throughput. We can simplify recovery on the assumption that there is no need to undo the effects of uncommitted transactions – these existed solely in-memory and had not yet been persisted to disk. (Just don’t try running such a system in a configuration with non-volatile memory!!). The command logging approach logs the operations (commands) that were executed, instead of the resulting data values. (Think Event Sourcing). Recovery then consists of replaying the sequence of commands. This clearly requires that commands are side-effect free, and also equates every command with a stored procedure (the transaction logic). This is the case in VoltDB on which the command-logging work is based.

Compared with an ARIES-style log, a command log is much more compact and hence reduces the I/O cost for materializing it onto disk. It has been shown that command logging can significantly increase the throughput of transaction processing in-memory databases…

For example, take a look at this graph of TPC-C throughput for single-node transactions where you can see command-logging giving throughput close to no logging at all, and ARIES style logging giving much reduced throughput:

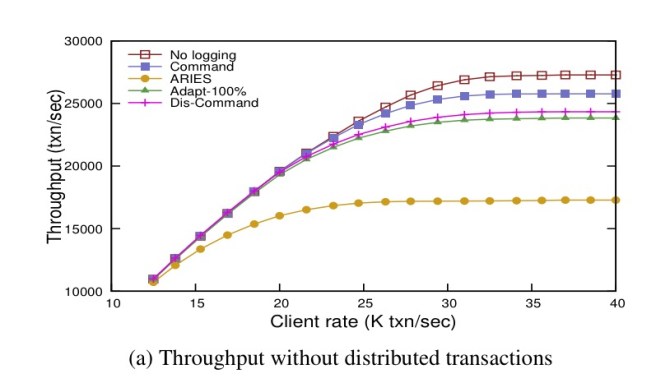
In contrast, when it comes time to recover from a failure, ARIES beats command-logging hands-down:

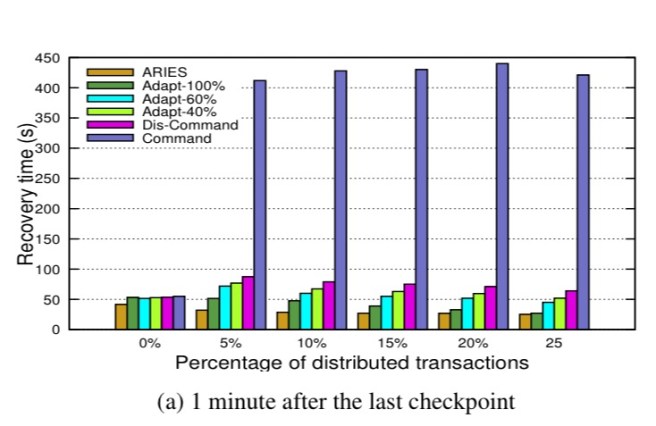
The situation becomes especially acute as we increase the mix of distributed transactions, and increase the distributed nature (number of nodes) of the datastore itself. Scale the datastore to enough nodes, such that the probability of failure of at least one node becomes high (i.e., we’re into ‘failure is the normal case’ territory) and recovery from command logs really loses out as it requires a merging of logs at a master node (no parallel recovery). Here’s an easy way to think about the ARIES recovery advantage: in an ARIES-style log, the log contains the post-commit value of a data item. So we can read the most recent value from the log and we’re done. But with a command log we can only reconstruct the current value by replaying all of the commands (at least, all of those since the last checkpoint).

You can probably see where this is going… for distributed in-memory datastores can we somehow achieve the high throughput of command logging, but with the fast (practical!) recovery of ARIES? That’s what ‘adaptive logging’ sets out to do…. Before we can get to that though, the first hurdle is to extend command-logging so that it can work well in an distributed setting.

Distributed command logging

In H-Store and its commercial successor, VoltDB, command logs of different nodes are shuffled to the master node that merges them based on timestamp order… Our intuition is to design a distributed command logging method that enables all nodes to start their recovery in parallel and replay only the necessary transactions.

I found this part of the paper (section 2) quite confusing. The overall intent is clear, but the details seem (to me at least) to be self-contradictory at points. (As an example, look at the first condition of transaction competition in definition 1, and the example transactions in figure 2. By my reading of that condition none of the transactions compete with each other – should it be \leq  instead of < ? And even if it is \leq that still wouldn’t account for t_6 competing with t_2 as my reading of figure 2 suggests it does??). I’ll do my best to give an interpretation here.

Each transaction has a given coordinator node. If a node fails, all of the transactions that node coordinated since the last checkpoint need to be recovered. But since we’re doing command logging, just replaying those transactions alone would not be enough. Consider a happens-before graph in which t_1 happens-before t_2 if t_1 writes a tuple that t_2 subsequently reads (and thus t_1 must also have committed before t_2 commits). We need to replay the transitive closure of transactions since the last checkpoint, under that happens-before relation, in their commit order. Call this set of transactions the recovery set.

Here’s an example from the paper, showing a set of transactions distributed across two nodes.

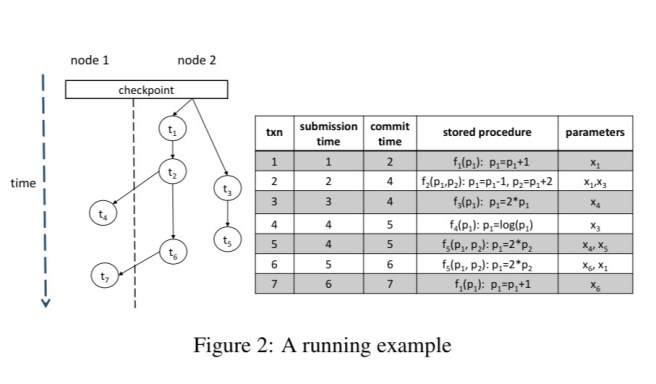
(Note a couple of things about that figure and the definitions in the paper: firstly, we need a global time-based ordering across nodes – VoltDB provides this. Secondly, note it’s very important that the parameters are pass-by-reference otherwise the association between ‘parameters’ and ‘tuples’ doesn’t make sense. Even then, it seems odd to me that a client could submit references to tuples as stored procedure parameters? And surely some parameter values can come from the outside otherwise we have a closed system? So I’m reading the RH column in figure 2 above as if the heading said ‘accessed tuples’ ).

I found it easier to see what’s going on with the following sketch, ymmv!

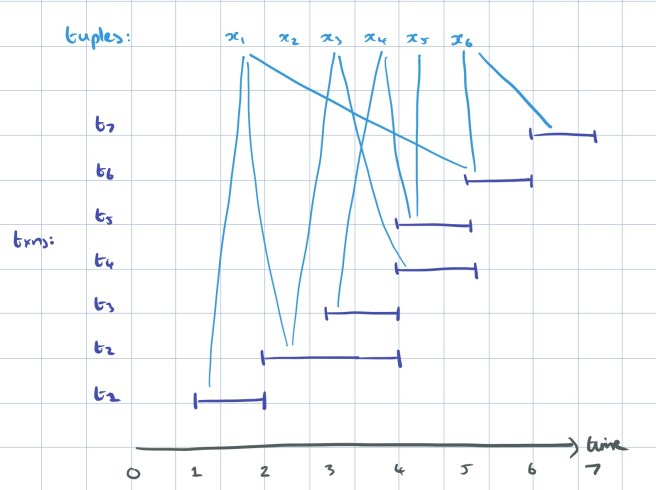
We can construct a dependency graph of the transactions in a recovery set with transactions as the nodes, and a directed edge from t_i to t_j if t_i happens-before t_j and no intervening transaction (i.e., sharing some of the same tuples) happens-before t_j. The root of the graph is a special node representing the last checkpoint, and its immediate children are therefore independent transactions and can be recovered in parallel, each being processed at its original coordinating node. In the example from figure 2 in the paper, if node 1 fails we will end up with transactions t_1, t_2, t_4, t_6, t_7 in the recovery set, and recovery will begin at node 2 with transaction t_1. (If node 2 had failed instead, we’d be able to initiate parallel recovery starting with transactions t_1 and t_3 on a newly started instance of node 2). The set of transactions in the transitive closure from one of these root transaction nodes in the dependency graph is called a processing group (so we have two potential processing groups in the running example). After processing the root transaction of a processing group, we can then initiate parallel recovery on all of its child transaction nodes, and so on until the tree is exhausted. For example, after replaying t_2, we could replay t_4 and t_6 in parallel (if both were in the recovery set and hence needed recovering).

With apologies to the authors if I messed up in my interpretation!

Adaptive distributed command logging

Now we’re back on solid ground! Note that when the dependency graph is shallow and wide we can get a high degree of parallelism in recovery (i.e., recover faster). But parts of the dependency graph that are narrow and deep require serial recovery. These latter parts of the graph would most benefit from ARIES style logging during recovery, as there is then no need to replay the whole processing group.

Hence, the intuition of our adaptive logging approach is to combine command logging and ARIES logging. For transactions that are highly dependent on the others, ARIES logs are created to speed up their reprocessing during the recovery. For other transactions, command logging is applied to reduce the logging overhead at runtime.

In the running example, if we have an ARIES log of t_7, there will never be a need to process t_6 during recovery of node 1. With adaptive logging, users specify an I/O budget that can be used during normal transaction processing, and the system selects the transactions that will most benefit from ARIES style logging within that budget. There’s just one small catch:

This decision of which type of logs to create for each transaction has to be made during transaction processing. However, since the distribution future of transactions cannot be known in advance, it is impossible to generate an optimal selection. In fact, even if we know all the future transactions, the optimization problem is still NP-hard.

Suppose we did know the distribution of future transactions. A reasonable (greedy) heuristic would be to order transactions by the expected recovery benefit of switching them to ARIES logging, and swap the logging strategy of the first n such transactions, up to the I/O budget.

Since the distribution of future transactions is unknown, we use a histogram to approximate the distribution. In particular, for all the attributes A = (a_0, …, a_k) involved in transactions, the number of transactions that read or write a specific attribute value is recorded. The histogram is used to estimate the probability of accessing an attribute a_i, denoted as P(a_i).

When processing a given transaction (the point in time at which we have to make the logging strategy decision) we also don’t know how many future transactions will follow it in the happens-before graph. Hence neither do we know how expensive command-log based recovery will be. The pragmatic solution for this is just to use a constant value for all transactions. We can then set a tunable expected benefit threshold. So long as we still have I/O budget available, an transactions that come along with an expected benefit above this threshold will be selected for ARIES logging.

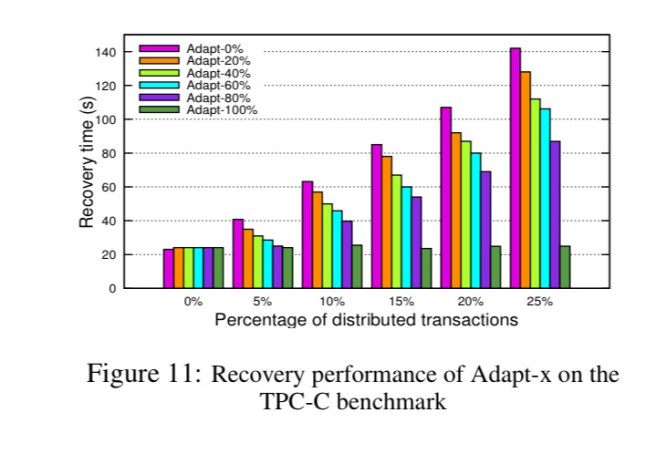
You can see the effect on recovery time of adapting differing percentages of transactions in the TPC-C benchmark to use ARIES logging in the following chart:

See the full paper for a detailed performance evaluation.