A Bayesian approach to graphical record linkage and de-duplication Steorts et al. AISTATS, 2014

I don’t normally cover papers from statistics conferences and journals, but this one caught my eye as addressing a high-value problem. Through a different lens, it also shows some of the challenges in maintaining privacy when it is possible to join data across multiple datasets.

Suppose you have several different datasets (or files using the terminology in the paper). The datasets don’t have any unique keys that allow you to join records across them. They were probably sourced independently, and possibly have some fields removed to protect privacy. As a concrete example (and probably the most common commercial use case), let’s say that each dataset concerns people. That is, every row in the dataset corresponds to some individual. Each dataset probably has some unique individuals in it that the others don’t, but we also assume that the same individual may appear in more than one dataset. We’d like to link rows in different datasets that all refer to the same individual. In the simplified version of the problem, each individual dataset does not contain duplicates (i.e. every row represents a different individual), but the algorithm the authors develop can also de-duplicate records within a single dataset.

When data about individuals comes from multiple sources, it is often desirable to match, or link, records from different files that correspond to the same individual. Other names associated with record linkage are entity disambiguation, entity resolution, and coreference resolution, meaning that records which are linked or co-referent can be thought of as corresponding to the same underlying entity.

The problem is made much harder due to the noise and distortions in typical data files (e.g. errors in entering ages, names, addresses and so on). There is a rich body of work in this field stretching back to at least 1969. The fundamental concept introduced in this this paper is that of a linkage structure, which can be used with a wide variety of models. In the paper itself the authors build a Bayesian model – the most basic and minimal member of the family. “We study it not for its realism but for its simplicity and to show what even such a simple model of the family can do.” The method can link records that do not have any identifying information (noisy or otherwise) such as name or address.

Take the following very basic example looking at three rows, one each from three different datasets:

          Gender:         State:   
File 1:   F               SC
File 2:   F               WV
File 3:   F               SC

Are we looking at three different women, or two? Or even one? How about now:

          Gender:         State:     DOB:
File 1:   F               SC         04/15/83
File 2:   F               WV         04/15/83    
File 3:   F               SC         07/25/43

The likelihood that the records from File 1 and File 3 represent the same real person has decreased…, record linkage is based on probabilities.

Here’s the setup: we have k different files (datasets), each with some number of rows j_k. The records in each dataset may have different fields, but there are p fields which all datasets share in common.

Let x_ij be the p-length categorical vector for the p fields of row j in dataset i.

Behind the datasets are some number of real people. In the worst case, every row of every dataset refers to a different person. If we add up the number of rows across all datasets we therefore get the maximum number of individuals, N_max. Let N be the actual number of distinct individuals (we don’t know N of course).

Let the (unknown) vector y_j’ be the p-length categorical vector for the true value of the p fields for the j’th person. Each x_ij is therefore a possibly distorted version of some y_j’.

Now we introduce the linkage structure Λ. Let λ_ij indicate which latent individual (real person) the j_th record in file _i refers to. Therefore x_ij is a possibly distorted version of y_λij.

To complete the model, let z_ijl be 1 or 0 according to whether or not a particular field l truly is distorted in x_ij.

This lets us model the following Bayesian parametric model:

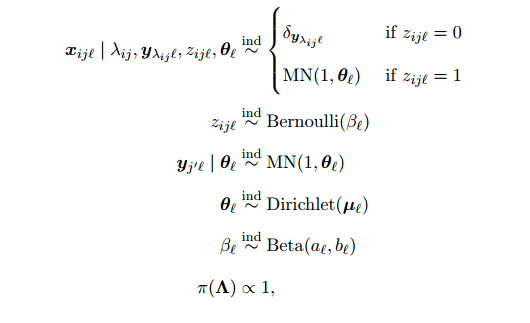
“Deriving the joint posterior and conditional distributions is mostly straightforward…” ;). See §3 of the paper if you’re interested in the details, my attempt at explaining them wouldn’t add much value.

What can we do with this model now we have it? We can use the Split and MErge REcord linkage and De-duplication algorithm (SMERED).

Our main goal is estimating the posterior distribution of the linkage (i.e., the clustering of records into latent individuals). The simplest way of accomplishing this is via Gibbs sampling. We could iterate through the records, and for each record, sample a new assignment to an individual (from among the individuals represented in the remaining records, plus an individual comprising only that record). However, this requires the quadratic-time checking of proposed linkages for every record. Thus, instead of Gibbs sampling, we use a hybrid MCMC (Markov chain Monte Carlo) algorithm to explore the space of possible linkage structures, which allows our algorithm to run in linear time.

SMERED can also take advantage of blocking, which simply requires an exact match in certain fields if records are to be linked.

In our application, we use an approximate blocking procedure, not an exact one. Since blocking gives up on finding truly co-referent records which disagree on those fields, it is best to block on fields that have little or no distortion. We block on the fairly reliable fields of sex and birth year in our application to the NLTCS below…

The core of the algorithm is actually very simple. On each iteration two records are chosen at random. If the pair currently belong to distinct latent individuals then a proposal is made to merge them to form a single new latent individual. If the pair currently belong to the same individual, then a proposal is made to split it into two latent individuals, each seeded with one of the two chosen records, and the other records randomly divided between the two. Proposed splits and merges are accepted based on the Metropolis-Hastings ratio and rejected otherwise.

Sampling from all possible pairs of records will sometimes lead to proposals to merge records in the same list. If we permit duplication within lists, then this is not a problem. However, if we know (or assume) there are no duplicates within lists, we should avoid wasting time on such pairs.

It’s tempting to say at the end of this process that if the posterior matching probability of two records exceeds some threshold, then they are linked. But this turns out not to work so well. Consider transitivity : if A and B are linked (represent the same individual), and B and C are linked, then A and C should also represent the same individual. Simple thresholding does not give us this property. Instead the authors consider maximal matching sets (MMSs). In an MMS every record in the set has the same value of λ_ij (points to the same latent individual), and no record outside of that set also points to λ_ij.

The MMSs allow a more sophisticated method of preserving transitivity when estimating a single overall linkage structure… Note, however there are still problems with a strategy of linking each record to exactly those other records in its most probably matching set. Specifically, it is possible for different records’ most probable maximal matching sets to contradict each other… To solve this problem we define a shared most probable MMS to be a set that is the most probably MMS of each of its members.

The final linkage structure links records if and only if there are in the same shared most probably MMS.

The output of the Gibbs sampler also allows us to estimate the value of any function of the variables, parameters, and linkage structure by computing the average value of the function over the posterior samples. For example, estimated summary statistics about the population of latent individuals are straightforward to calculate.

Evaluation

The model was tested using data from the National Long Term Care Survey (NLTCS), a longitudinal study of the health of elderly individuals. The survey was conducted every six years, comprising about 20,000 individuals each time.

To show how little information our method needs to find links across files, we gave it access to only four variables, all known to be noisy: date of birth, sex, state of residence, and the regional office at which the subject was interviewed. We linked individuals across the 1982, 1989 and 1994 survey waves.

Of course, the full data set also includes unique identifiers, so the authors could test how well their matching performed. The false negative rate was 0.11, and the false positive rate is 0.046, when blocking by date of birth year and sex.

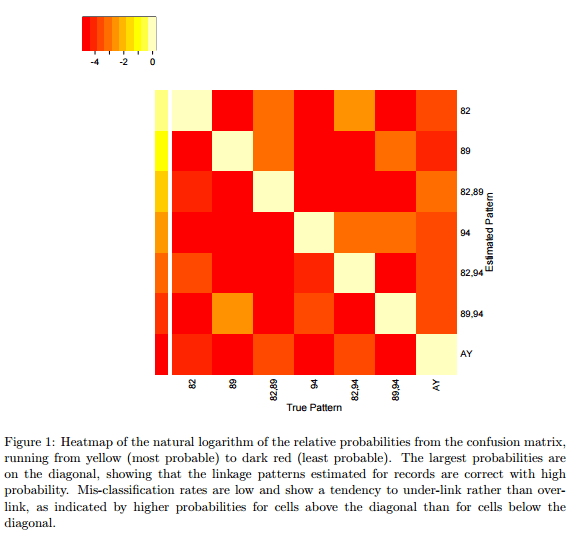
Here’ a neat visualization of the resulting linkage structure for 204 records. Nodes are records, and edges join records with shared MMSs. Green edges indicate high confidence, red edges low confidence, and wavy edges where the model actually got it wrong compared to the ground truth.

SMERED is comparatively fast too – it matched the NLTCS study datasets in three hours, whereas the alternative method of Tancredi and Liseo would take approximately 62 days!