Towards deep symbolic reinforcement learning Garnelo et al, 2016

Every now and then I read a paper that makes a really strong connection with me, one where I can’t stop thinking about the implications and I can’t wait to share it with all of you. For me, this is one such paper.

In the great see-saw of popularity for artificial intelligence techniques, symbolic reasoning and neural networks have taken turns, each having their dominant decade(s). The popular wisdom is that data-driven learning techniques (machine learning) won. Symbolic reasoning systems were just too hard and fragile to be successful at scale. But what if we’re throwing the baby out with the bath water? What if instead of having to choose between the two approaches, we could combine them: a system that can learn representations, and then perform higher-order reasoning about those representations? Such combinations could potentially bring to bear the fullness of AI research over the last decades. I love this idea because:

(a) it feels intuitively right (we as humans learn to recognise types of things, and then form probability-based rules about their behaviour for example);

(b) it is very data efficient, to appropriate a phrase:  “a rule can be worth 1000(+) data points!”

(c) it opens up the possibility to incorporate decades of research into modern learning systems, where you can’t help but think there would be some quick wins.

… we show that the resulting system – though just a prototype – learns effectively, and, by acquiring a set of symbolic rules that are easily comprehensible to humans, dramatically outperforms a conventional, fully neural Deep Reinforcement Learning system on a stochastic variant of the game.

In short, this feels to me like something that could represent a real breakthrough and a step-change in the power of learning systems. You should take that with a pinch of salt, because I’m just an interested outsider following along. I hope that I’m right though!

Why combine symbolic reasoning and deep learning?

Contemporary Deep Reinforcement Learning (DRL) systems achieve impressive results but still suffer from a number of drawbacks:

1. They inherit from deep learning the need for very large training sets, so that they learn very slowly
2. They are brittle in the sense that a trained network that performs well on one task often performs poorly on a new task, even if it is very similar to the original one.
3. They do not use high-level processes such as planning, causal reasoning, or analogical reasoning to fully exploit the statistical regularities present in the training data.
4. They are opaque – it is typically difficult to extract a human-comprehensible chain of reasons for the action choice the system makes .

In contrast, classical AI uses language-like propositional representations to encode knowledge.

  Thanks to their compositional structure, such representations are amenable to endless extension and recombination, an essential feature for the acquisition and deployment of high-level abstract concepts, which are key to general intelligence. Moreover, knowledge expressed in propositional form can be exploited by multiple high-level reasoning processes and has general-purpose application across multiple tasks and domains. Features such as these, derived from the benefits of human language, motivated several decades of research in symbolic AI. But as an approach to general intelligence, classical symbolic AI has been disappointing. A major obstacle here is the symbol grounding problem…

The symbol grounding problem is this: where do the symbols come from? They are typically hand-crafted rather than grounded in data from the real world. This brings a number of problems:

• They cannot support support ongoing adaptation to a new environment
• They cannot capture the rich statistics of real-world perceptual data
• They create a barrier to full autonomy

Machine learning has none of these problems!

So what if we could take the good bits from machine learning, and combine them with the good bits from classical AI? Use machine learning to learn symbolic representations, and then use symbolic reasoning on top of those learned symbols for action selection (in the case of DRL).

You end with a system architecture that looks like this:

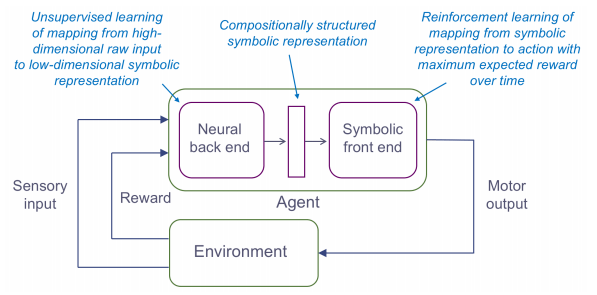
Four principles for building Deep Symbolic Reinforcement Learning (DSRL) systems

1. Support conceptual abstraction by mapping high-dimensional raw input into a lower dimensional conceptual state space, and then using symbolic methods that operate at a higher level of abstraction.  “This facilitates both data efficient learning and transfer learning as well as providing a foundation for other high-level cognitive processes such as planning, innovative problem solving, and communication with other agents (including humans).
2. Enable compositional structure that supports combining and recombining elements in an open-ended way.  “To handle uncertainty, we propose probabilistic first-order logic for the semantic underpinnings of the low-dimensional conceptual state space representation onto which the neural front end must map the system’s high-dimensional raw input.
3. Build on top of common sense priors – it is unrealistic to expect an end-to-end reinforcement learning system to succeed with no prior assumptions about the domain. For example: objects frequently move, and typically do so in continuous trajectories, there are stereotypical events such as beginning to move, stopping, coming into contact with other objects, and so on.
4. Support causal reasoning through discovery of the causal structure of the domain and symbolic rules expressed in terms of both the domain and the common sense priors.

To carry out analogical inference at a more abstract level, and thereby facilitate the transfer of expertise from one domain to another, the narrative structure of the ongoing situation needs to be mapped to the causal structure of a set of previously encountered situations. As well as maximising the benefit of past experience, this enables high-level causal reasoning processes to be deployed in action selection, such as planning, lookahead, and off-line exploration (imagination).

A worked example

Well it all sounds good, but does it actually work? The prototype system built by the authors learns to play four variations on a simple game. An agent moves around a square space populated by circles and crosses. It receives a positive reward for every cross it ‘collects’, and a negative reward for every circle. Four variations are used: the first has only circles in a fixed grid, the second both circles and crosses in a fixed grid, the third only circles but in a random grid, and the fourth both circles and crosses in a random grid.

The system has three stages: low-level symbol generation, representation building, and reinforcement learning.

The first stage use a convolutional neural network (autoencoder) trained on 5000 randomly generated images on game objects scattered across the screen. The activations in the middle layer of the CNN are used directly for detection of objects in the scene. The salient areas in an image result in higher activation throughout the layers of the convolutional network. Given the geometric simplicity of the games, this is enough to extract the individual objects from any given frame.

The objects identified this way are then assigned a symbolic type according to the geometric properties computed by the autoencoder. This is done by comparing the activation spectra of the salient pixels across features.

At this point we know the type and position of the objects.

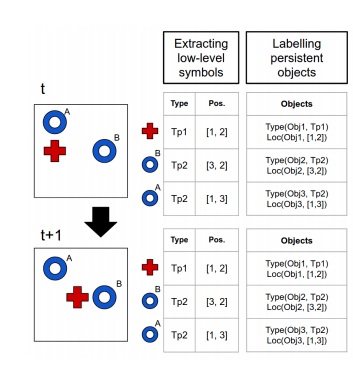
The second stage learns to track objects across frames in order to learn from their dynamics. The system is supported in this task by a common sense prior, “object persistence over time”. This is broken down into three measures ultimately combined into a single value: how close an object in one frame is to an object in another frame (spatial proximity is an indicator it may be the same object); how likely it is that an object transformed from one type into another (by learning a transition probability matrix); and what change there is in the neighbourhood  of an object.

The representation learned at the end of the second stage differs from that of the first stage in two key ways:

1. It is extended to understand changes over time, and
2. Positions of objects are represented by relative coordinates to other objects rather than using absolute coordinates. “This approach is justified by the common sense prior that local relations between multiple objects are more relevant than the global properties of single objects.”

We  now have a concise spatio-temporal representation of the game situation, one that captures not only what objects are in the scene along with their locations and types, but also what they are doing. In particular, it represents frame-to-frame interactions between objects, and the changes in type and relative position that result. This is the input to reinforcement learning, the third and final stage of the pipeline.

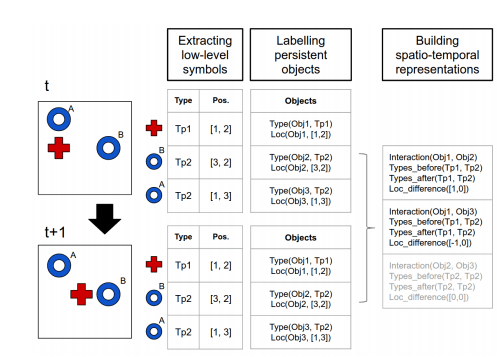
Finally we enter the reinforcement learning stage, where the relative location representation of objects greatly reduces the state space, on the assumption that things that are far apart (both in the game and in the real world) tend to have little influence on each other.

In order to implement this independence we train a separate Q function for each interaction between two object types. The main idea is to learn several Q functions for the different interactions and query those that are relevant for the current situation. Given the simplicity of the game and the reduced state space that results from the sparse symbolic representation we can approximate the optimal policy using tabular Q-learning.

Evaluation results

You can use precision and recall metrics to evaluate agent performance – where precision is interpreted as the percentage of objects you collect that are positive (crosses), and recall is interpreted as the percentage of available positive objects that you actually do collect.

The first results show that the agent improves with training to a precision of 70%. It’s interesting to compare the performance of DQN and the DSRL system. DQN does better in the the grid scenario, but when objects are position at random the DQN agent struggles to learn an effective policy within 1000 epochs. The DSRL system performs much better on this variant:

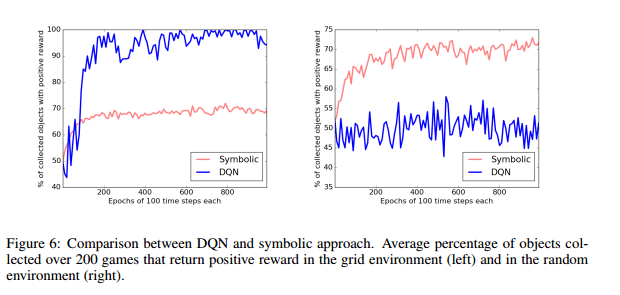
To evaluate transfer learning, both DQN and DSRL were trained on the grid variation, and then tested on the random variant.  DQN does no better than chance, whereas the DSRL system is able to approach 70% precision.

  We conjecture that DQN struggles with this game because it has to form a statistical picture of all possible object placements, which would require a much larger number of games. In contrast, thanks to the conceptual abstraction made possible by its symbolic front end, our system very quickly “gets” the game and forms a set of general rules that covers every possible initial configuration. This demonstration merely hints at the potential for a symbolic front end to promote data efficient learning, potential that we aim to exploit more fully in future work. Our proof-of-concept system also illustrates one aspect of the architecture’s inherent capacity for transfer learning…

Moreover, the DSRL system can explain its actions: every action choice can be analysed in terms of the Q functions involved in the decision. These Q functions describe the types of objects involved in the interaction as well as their relations, so we can track back to the reasons that led to a certain decision.

And this is just the beginning…

• We could wire in a more sophisticated deep network capable of unsupervised learning to disentangle representations in the earlier stages.
• We can exploit many more of the achievements in classical AI, notably the incorporation of inductive logic programming, formal techniques for analogical reasoning, and building in a planning component that exploits the knowledge of the cause structure of the domain acquired during the learning process.

  In domains with sparse reward, it’s often possible for an agent to discover a sequence of actions leading to a reward state through off-line search rather than on-line exploration. Contemporary logic-based planning methods are capable of efficiently finding large plans in complex domains (eg:[37]), and it would be rash not to exploit the potential of these techniques.

• Finally, one day the symbolic components of the proposed architecture could well be one day using neurally-based implementations of symbolic reasoning functions.

In the mean time, an architecture that combines deep neural networks with directly implemented symbolic reasoning seems like a promising research direction.