Reducing Crash Recoverability to Reachability – Koskinen & Yang 2016.

Techniques such as shadow paging and write-ahead logging can help with recovery from crashes, but even then it takes a lot of sophistication to get it right and deal with cases such as crashing during recovery itself. In today’s paper Koskinen and Yang first provide us with a definition of what it means for a program to be crash recoverable. Based on this definition, they then show how to prove that a program can correctly recover from a crash. That’s good, but the next bit is really good: they wrote a tool called Eleven82 that can analyse an existing C program (Java soon) to detect existing recoverability bugs or prove their absence!

Our tool is able to prove recoverability for programs that implement complex filesystem algorithms such as write-ahead logging and shadow paging We have applied our implementation to benchmark examples taken from several industrial databases, virtual machine monitors, and distributed consensus servers including GDBM, LevelDB, LMDB, PostgreSQL, SQLite, VMware and ZooKeeper. Our tool is able to automatically discover (known) recoverability bugs or prove recoverability of these examples, and it is typically able to do so within a minute or two.

A crash is simply some kind of external event that ‘havocs’ (destroys) volatile storage but maintains persistent storage (the formal model doesn’t actually require this latter condition). After a crash, a recovery process runs which establishes a (potentially new) initial state – perhaps with the help of an auxiliary recovery script. Normal execution of the program then resumes. (Many recovery schemes allow execution to resume while recovery is still ongoing in the background, but we won’t consider that optimisation here). A central hypothesis of the paper is that:

Recovered programs should not introduce behaviors that were not present in the original (uncrashed) program.

Consider the following program fragment:

 in = open(input);
 out = open(output, O_CREAT | O_WRONLY);
 write(out,"A");
 // CRASH HERE
 ...

Suppose the program crashes immediately after making the write call – we could be left in one of three states:

1. output does not exist
2. output exists but is empty
3. output exists and contains the single byte “A”

   If we restart the program in case (2) or (3) it won’t behave as it did before.

With the possibility of crashes comes the possibility that new behaviors will be introduced during re-execution. Programs that are able to properly recover from a crash need to account for these new situations that may arise: when the program is re-executed, some operations will have become persistent and volatile data will be lost. By including the O_TRUNC flag we make the program crash recoverable: when re-executed, the program overwrites the incomplete modifications from the first execution.

Consider all of the possible traces [[P]] of a program P. Let P̂ be a program that is identical to P except that it may crash at any point and be re-executed. We want to show that [[P̂]] ⊆ [[P]] modolu some simulation relation. This simulation relation ≽ relates states in P to states in P̂. Using σ to represent a program state, we define σ ≽ σ′ to mean that the states σ and σ′ are observationally equivalent. In other words, from an external perspective we can’t tell the difference between an execution of the recovered program, and an execution of the original (un-crashed program). It doesn’t have to simulate exactly what the first execution did (pre-crash), but it must simulate some feasible execution of the program.

A key benefit of this approach to crash recoverability is that we can use the original program as the specification for how the program should behave in the context of crashes.

Recovery proofs take the following form. Consider a program that moves through states σ₀ → σ₁ → σ₂ → … → σ_n, at which point it crashes. The crash transitions the program to some state σ′ from which recovery is needed. A correct recovery eventually leads to some state σ̄_k, which is observationally equivalent to some state σ_k in the original trace (σ_k ≽ σ̄_k). Hence forward, the system behaves as if it had not crashed.

We found that this definition was suitable to cover a wide variety of examples taken from the industrial systems that we considered.

Using R₀ to represent the program that can recover from zero crashes (true by definition) then inductive and co-inductive rules are shown for programs that can recovery from N crashes (R_N, or N-recoverability) and an infinite number of crashes (∞-recoverability).

To automate discovering proofs of recoverability an input program is transformed into a control flow automaton Α (Eleven82 is built upon the CPAchecker tool). This input automation is then further transformed (see the paper for details) into a new automation written Α_ε^D. This new automaton includes a special state q_err. It is possible to reach this state if it is possible for crash-recovery to diverge or lead to a state that is not observationally equivalent to some prefix state in the original program execution. Therefore, a non-reachability proof for Α_ε^D entails crash recoverability of &Alpha. Hence the title of the paper, “_Reducing crash recoverability to reachability.”

Our prototype implementation transforms input programs via C preprocessor macro replacements for libc operations. These macros instantiate a model file system (discussed next), create the cross product with the asynchronous operations, and perform the transformation described [above].

The model filesystem is carefully designed to work around the limitations of the CPAchecker which does not understand tree structures (e.g. directory hierarchies) and does not support quantified invariants (forall…).

The following table shows the results of the evaluation apply the crash-recovery checker to real programs. The ‘Var’ column describes variants of the original program – often introduced because the first run showed that the program was not in fact crash recoverable. LOC is the lines of code in the original C program, and XLOC in the generated encoding. Q represents the number of states in the automaton. The SMT column shows which SAT solver was used: SMTInterpol as first choice, and MathSAT where SMTInterpol could not handle the input. Time is the time taken to verify the input. Exp shows the expected results (whether the program should be reported as crash-recoverable or not), and Res. the actual result.

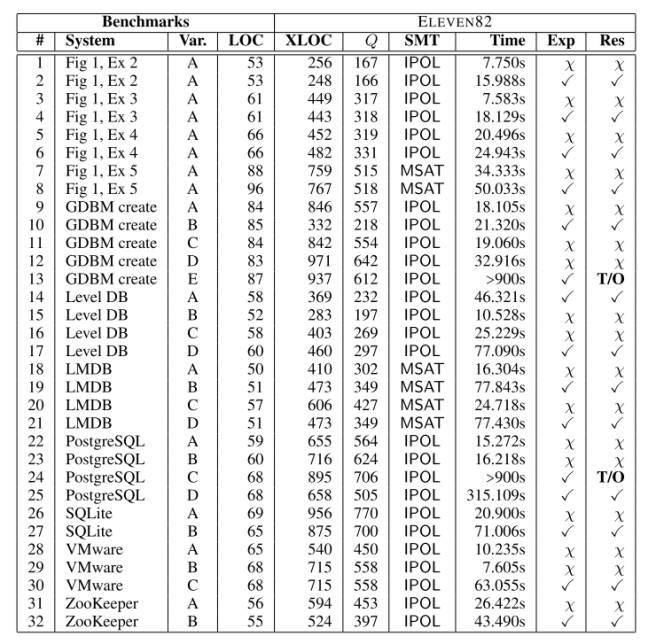
In all but two cases, we were able to prove crash recoverability (or find a counterexample) in a minute or two. The PostgreSQL variant C and GDBM variant E timed out after the 900s CPAchecker default limit. Some benchmarks included complex recovery scripts. In the LevelDB example, the recovery script examines the disk’s entry for a file new_log and, depending on what version was last written, recovers to the appropriate location in the program, which may be in the middle of a loop.Our benchmarks helped us realize that the file descriptor COUNTER needs to be included in the snapshots in addition to the disk and memory. We also realized that when a file is created, the disk file version should initially be the same as the memory initial version. We found the counterexamples generated by ELEVEN82 to be very helpful, as they allow one to trace back and discover why the simulation broke down.