Arabesque: A System For Distributed Graph Mining – Teixeira et al. 2015
We’ve studied graph computation systems before in The Morning Paper: systems such as Pregel, Giraph and GraphLab that provide vertex-centric programming models (‘think like a vertex’) on top of a Bulk Synchronous Parallel compute model. We’ve also seen some of the limitations of the vertex-centric constraint and the dangers of being constrained by a programming model and hence tempted into adopting inefficient algorithms for the problem at hand.
Arabesque looks at the graph mining problem of finding relevant patterns in graphs based on structural or label properties.
Designing graph mining algorithms is a challenging and active area of research. In particular, scaling graph mining algorithms to even moderately large graphs is hard. The set of possible patterns and their subgraphs in a graph can be exponential in the size of the original graph, resulting in an explosion of the computation and intermediate state.
Arabesque defines an efficient alternative programming model for graph mining described as ‘think like an embedding’ (TLE), that is also built on top of an underlying Bulk Synchronous Parallel compute model. The implementation is built as an extension to Apache Giraph. The Arabesque system and all the applications discussed in the paper are available at www.arabesque.io.
Before we dive in, I’d just like to take a moment to commend the authors on the clarity of their writing and presentation. As someone familiar with graph processing, but not especially with the state of the art in graph mining, I learned a huge amount from the paper and very much appreciated the way the necessary background was laid out. If you have time or inclination, it’s well worth reading this paper in its entirety.
Graph Mining Background
Graph mining is widely used for several applications, for example, discovering 3D motifs in protein structures or chemical compounds, extracting network motifs or significant subgraphs from protein-protein or gene interaction networks, mining attributed patterns over semantic data (e.g., in Resource Description Framework or RDF format), finding structure-content relationships in social media data, dense subgraph mining for community and link spam detection in web data, among others…
Starting with a labelled and immutable graph, mining algorithms look for all instances of some pattern within the graph, and possibly also computing aggregate metrics on these graphs.
Designing graph mining algorithms is a challenging and active area of research. In particular, scaling graph mining algorithms to even moderately large graphs is hard… Even graphs with few thousands of edges can quickly generate hundreds of millions of interesting subgraphs. The need for enumerating a large number of subgraphs characterizes graph mining problems and distinguishes them from graph computation problems. Despite this state explosion problem, most graph mining algorithms are centralized because of the complexity of distributed solutions.
A subgraph of the input graph is called an embedding. Embeddings may be created by starting with a set of vertices (vertex induced), or with a set of edges (edge induced). A pattern is an arbitrary graph (think of it like a template for mining). A pattern is isomorphic to an embedding if there is a one-to-one mapping between the vertices and edges in the pattern and the embedding.
The paper examines three different graph mining problems that are representative of different classes of graph mining problems: frequent subgraph mining, counting motifs, and finding cliques. Frequent subgraph mining requires finding patterns that occur a minimum number of times in the input set. In the counting motif problem, the goal is to find the set of all distinct motifs in an input graph, together with their frequencies. A motif is ‘a connected pattern of vertex-induced embeddings.’ In clique mining, the goal is to enumerate all connected subgraphs of k vertices where each vertex has degree k-1 (i.e. connected to all others.
Think like a vertex, a pattern, or an embedding?
The standard paradigm of systems like Pregel is vertex-centric or “Think Like a Vertex” (TLV), because computation and state are at the level of a vertex in the graph. TLV systems are designed to scale for large input graphs: the information about the input graph is distributed and vertices only have information about their local neighborhood.
Using the TLV model for computing embeddings requires ‘growing’ embeddings from each starting vertex. Highly connected vertices end up with disproportionate load, and many duplicate embeddings are created. Given the already exponential issue with embeddings, this is not good… TLV is two orders of magnitude slower than Arabesque for example.
The current state-of-the-art centralized methods for solving graph mining tasks typically adopt a different, pattern-centric or “Think Like a Pattern” (TLP) approach. The key difference between TLP and the embedding-centric view of the filter-process model is that it is not necessary to explicitly materialize all embeddings: state can be kept at the granularity of patterns (which are much fewer than embeddings) and embeddings may be re-generated on demand.
The issue with TLP is that it is hard to parallelize effectively since there are often only a few patterns that are highly popular.
Arabesque uses an approach the authors call ‘think like an embedding’ (TLE).
Given an input graph, the system takes care of automatically and systematically visiting all the embeddings that need to be explored by the user-defined algorithm, performing this exploration in a distributed manner. The system passes all the embeddings it explores to the application, which consists primarily of two functions: filter, which indicates whether an embedding should be processed, and process, which examines an embedding and may produce some output. For example, in the case of finding cliques the filter function prunes embeddings that are not cliques, since none of their extensions can be cliques, and the process function outputs all explored embeddings, which are cliques by construction. Arabesque also supports the pruning of the exploration space based on user-defined metrics aggregated across multiple embeddings.
The Arabesque programming model
An Arabesque computation proceeds through a series of exploration steps, using a Bulk Synchronous Parallel (BSP) model.
Each step is associated with an initial set I containing embeddings of the input graph G. Arabesque automates the process of exploring the graph and expanding embeddings. Applications are specified via two user-defined functions: a filter function φ and a process function π. The application can optionally also define two additional functions that will be described shortly…
Arabesque can be set to run in edge-based or vertex-based exploration mode. In the very first iteration, each edge (or vertex respectively) is a candidate embedding, and at each step the system creates candidate embeddings by adding one edge (or vertex, for vertex-based exploration). Each candidate embedding is passed to the user-defined filter function φ. If the filter function returns true, then the embedding e’ is passed to the user-defined process function π, which may produce some output to be aggregated. The set of filtered embeddings, F, then become the new input for the next step. Computation is terminated when F is empty at the end of a step.
Each step is run in parallel by partitioning the embeddings across a set of servers. Steps are executed as supersteps in the BSP model.
A common task in graph mining systems is to aggregate values across multiple embeddings, for example grouping embeddings by pattern. To this end, Arabesque offers specific functions to execute user-defined aggregation for multiple embeddings. Aggregation can group embeddings by an arbitrary integer value or by pattern, and is executed on candidate embeddings at the end of the exploration step in which they are generated. The optional aggregation filter function α and aggregation process function β can filter and process an embedding e in the exploration step following its generation. At that time, aggregated information collected from all the embeddings generated in the same exploration step as e becomes available.
Arabesque requires an anti-monotonicity property to hold:
if φ(e) = false then it holds that φ(e’) = false for each embedding e’ that extends e. The same property holds for the optional filter function α. This is one of the essential properties for any effective graph mining method and guarantees that once a filter function tells the framework to prune an embedding, all its extensions can be ignored.
Using the Arabesque API, the authors were able to implement frequent sub-graph mining in 280 lines of Java code (most of it support functions needed to characterize whether an embedding is relevant – which would be needed in any implementation). The centralized baseline used for comparison, GRAMI, requires 5,433 lines of Java code.
The motif frequency computation requires 18 lines of code, compared to the 3,145 lines of C in the baseline Gtries system. The basic structure is:
boolean filter(Embedding e){
return (numVertices(e) <= MAX_SIZE);
}
void process(Embedding e){
mapOutput (pattern(e),1);
}
Pair reduceOutput(Pattern p, List counts){
return Pair (p, sum(counts));
}
Some of these algorithms are the first distributed solutions available in the literature, which shows the simplicity and generality of Arabesque.
Implementation challenges of note
Arabesque can execute on top of any system supporting the BSP model. We have implemented Arabesque as a layer on top of Giraph. The implementation does not follow the TLV paradigm: we use Giraph vertices simply as workers that bear no relationship to any specific vertex in the input graph. Each worker has access to a copy of the whole input graph whose vertices and edges consist of incremental numeric ids. Communication among workers occurs in an arbitrary point-to-point fashion and communication edges are not related to edges in the input graph.
Some of the challenges that the team had to overcome during the implementation include:
- Pruning duplicate embeddings without requiring coordination between nodes
- Finding a compact representation for embeddings, and
- Optimizing per-pattern aggregations.
It’s possible to grow the same embedding in multiple ways (for example, start with vertex v1 and then add vertex v2, or start at vertex v2 and then add vertex v 1). To avoid processing such automorphic embeddings multiple times, defines a canonical form for an embedding. If a candidate embedding is not canonical, it is automatically pruned by the framework and never passed to the user’s code. The canonical form for an embedding is one in which the vertices where visited in ascending order of id.
Because there can be a large number of embeddings passed between supersteps (“Graph mining algorithms can easily generate trillions of embeddings as intermediate state”), it’s important to find a compact representation for them.
Arabesque represents embeddings as sequences of numbers, representing vertex or edge ids depending on whether exploration is vertex-based or edge-based. Therefore, we need to find techniques to store sets of sequences of integers efficiently. Existing compact data structures such as prefix-trees are too expensive because we would still have to store a new leaf for each embedding in the best case, since all canonical embeddings we want to represent are different. In contrast, Arabesque uses a novel technique called Overapproximating Directed Acyclic Graphs, or ODAGs. At a high level, ODAGs are similar to prefix trees where all nodes at the same depth corresponding to the same vertex in the graph are collapsed into a single node. This more compact representation is an overapproximation (superset) of the set of sequences we want to store. When extracting embeddings from ODAGs we must do extra work to discard spurious paths. ODAGs thus trade space complexity for computational complexity.
Suppose we’ve reached step three in exploring the embeddings for the following graph.
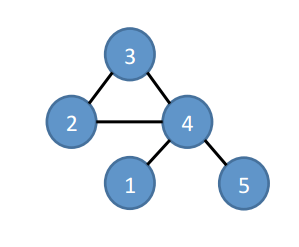
We’d have a set of canonical embeddings (all vertices in ascending order) like this:
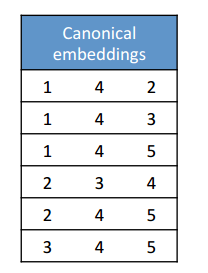
The ODAG structure would encode as follows:
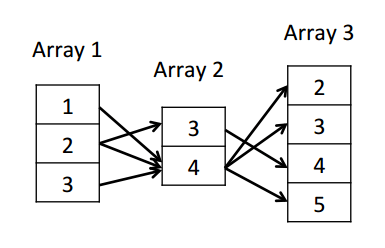
Canonical embeddings can be recreated by traversing every path from the first column to the third.
It is possible to obtain all embeddings of the original set by simply following the edges in the ODAG. However, this will also generate spurious embeddings that are not in the original set….
These spurious embeddings can be filtered out using the user-provided φ (filter) function.
Per-pattern aggregation has a high potential cost, and so Arabesque uses a two-stage process for this. Consider the desire to aggregate embeddings that contain both a blue and a yellow endpoint….
… assume that we want to count the instances of all single-edge patterns. The three single-edge embeddings (1, 2), (2, 3), and (3, 4) should be aggregated together since they all have a blue and a yellow endpoint. Therefore, their two patterns (blue, yellow) and (yellow, blue) should be considered equivalent because they are isomorphic. The aggregation reducer for these two patterns
is associated to a single canonical pattern that is isomorphic to both. Mapping a pattern to its canonical pattern thus entails solving the graph isomorphism problem, for which no polynomial-time solution is known. This makes pattern canonicality much harder than embedding canonicality, which is related to the simpler graph automorphism problem.
Arabesque first executes the reduce function based on ‘quick’ patterns, which ignore isomorphism (I.e., (blue,yellow) and (yellow,blue) are reduced independently). Then a worker computes the canonical pattern _pc for each quick pattern and sends the locally aggregated value to the reducer for _pc.
Evaluation…
Overall, the results show that even with the commodity servers that we utilize, Arabesque can process graphs that are dense and have hundreds of millions of edges and tens of million of vertices.
Even on a single thread (remember CoST?), Arabesque can match or beat application-specific implementations:
These results are a clear indicator of the efficiency of Arabesque. Despite being built with a generic framework running over Hadoop (and Java), Arabesque can achieve performance comparable, and sometimes even superior, to application-specific implementations. The main contributing factor, as we show later in this section, is that the user-defined functions in Arabesque consume an insignificant amount of CPU time. The user-defined functions steer the exploration process through a high-level API. The API abstracts away the details of the actual exploration process, which are under the control of Arabesque and can thus be efficiently implemented. This is in stark contrast to the graph processing systems analyzed in [27], where the user-defined functions perform the bulk of the computation, leaving little room for system-level optimizations.
But of course, the underlying BSP computation model also makes it easy to scale the system to a large number of servers…
3 thoughts on “Arabesque: A System for Distributed Graph Mining”
Comments are closed.