Reactive Vega: A Streaming Dataflow Architecture for Declarative Interactive Visualization – Satyanarayan et al. 2015
Today’s paper choice combines Event-driven FRP (E-FRP) with dataflow and stream management techniques from the database community to implement declarative interactive visualisations on top of the existing Vega declarative visualisation grammar and supporting runtime.
As a good example of what’s possible, take a look at this interactive visualization of US airports in the Live Vega Editor:
(Note the “signals” section in the mark-up).
In contrast with existing reactive visualization toolkits where only interaction events are modeled as time-varying, Reactive Vega features a unified data model in which the input data, scene graph elements, and interaction events are all treated as first-class streaming data sources.
Functional Reactive Programming (FRP) models mutable values as continuous, time-varying data streams. We focus on a discrete variant called Event-Driven FRP (E-FRP). To capture value changes as they occur, E-FRP provides streams, which are infinite time-ordered sequences of discrete events. Streams can be composed into signals to build expressions that react to events. The E-FRP runtime constructs the necessary dataflow graph such that, when a new event fires, it propagates to corresponding streams. Dependent signals are evaluated in a two-phase update: signals reevaluated in the first phase use prior computed values of their dependents, which are subsequently updated in the second phase.
To efficiently support relational data, Reactive Vega integrates methods from the streaming database literature (Aurora, Eddies, STREAM, TelegraphCQ, Borealis). And to support streaming hierarchical data, Reactive Vega’s dataflow graph dynamically rewrites itself at runtime, instantiating new branches to process nested relations.
In Vega’s declarative visualization design, visual encodings are defined by composing graphical primitives called marks (arcs, bars, lines, symbols and text for example).
Marks are associated with datasets, and their specifications describe how tuple values map to visual properties such as position and color. Scales and guides (i.e., axes and legends) are pro- vided as first-class primitives for mapping a domain of data values to a range of visual properties. Special group marks serve as containers to express nested or small multiple displays. Child marks and scales can inherit a group mark’s data, or draw from independent datasets.
Here’s a declarative specification for a brushing interaction:
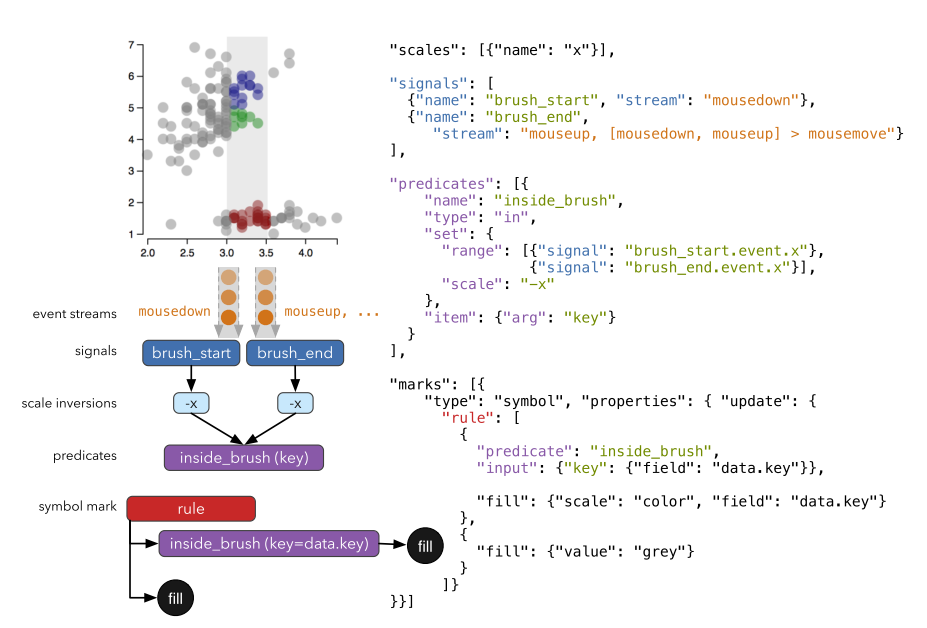
Our approach draws on Event- Driven Functional Reactive Programming (E-FRP) to abstract input events as time-varying streaming data. An event selector syntax facilitates composing and sequencing events together, for example ‘[mousedown, mouseup] > mousemove’ is a single stream of mousemove events that occur between a mousedown and mouseup (i.e., “drag” events). Event streams are modeled as first-class data sources and can thus drive visual encoding primitives, or be run through the full gamut of data transformations. For added expressivity, event streams can be composed into reactive expressions called signals. Signals can be used directly to specify visual primitive properties. For example, a signal can dynamically determine a mark’s fill color or a scale’s domain. Signals can also parameterize interactive selection rules for visual elements called predicates. Predicates define membership within the selection (e.g., by specifying the conditions that must hold true) and can be used within sequences of production rules to drive conditional visual encodings.
Under the Covers
Dataflow operators are instantiated and connected by the Reactive Vega parser, which traverses a declarative specification containing definitions for input datasets, visual encoding rules, and interaction primitives as described in § 3. When data tuples are observed, or when interaction events occur, they are propagated (or “pulsed”) through the graph with each operator being evaluated in turn. Propagation ends at the graph’s sole sink: the renderer.
As each dataset definition is parsed, a corresponding branch in the dataflow graph is constructed. The branches contain input and output nodes connected by a pipeline of data transformation operators.
Input nodes receive raw tuples as a linear stream (tree and graph structures are supported via parent-child or neighbor pointers, respectively). Upon data source updates, tuples are flagged as either added, modified, or removed, and each tuple is given a unique identifier. Data transformation operators use this metadata to perform targeted computation and, in the process, may derive new tuples from existing ones. Derived tuples retain access to their “parent” via prototypal inheritance. This relieves operators of the burden of propagating unrelated upstream changes.
For every low-level event type required by the visualization (e.g. mousedown events) Vega instantiates an event listener node in the dataflow graph and directly connects it to dependent signals.
In the case of ordered selectors (e.g., a “drag” event specified by ‘[mousedown, mouseup] > mousemove’), each constituent event is connected to an automatically created anonymous signal; an additional anonymous signal connects them to serve as a gatekeeper, and only propagates the final signal value when appropriate. Individual signals can be dependent on multiple event nodes and/or other signals, and value propagation follows E-FRP’s two-phase update.
Generated scene graph elements are themselves modeled as data tuples, and thus can serve as the input data for further downstream visual encoding primitives. This enables higher-level layout algorithms to be expressed in a fully declarative fashion. The authors describe this as reactive geometry.
Glitches are avoided through the use of a centralized dataflow graph scheduler that dispatches changesets to appropriate operators in topological order, thus ensuring that an operator is only evaluated after all of its dependencies are up to date. This centralization also allows more aggressive pruning of unnecessary computation:
(a) As the scheduler ensures a topological propagation ordering, a branch can be safely pruned for the current propagation if it has already been reflowed… (b) Skipping unchanged operators: Operators identify their dependencies—including signals, data fields, and scale functions—and changesets maintain a tally of updated dependencies as they flow through the graph. The scheduler skips evaluation of an individual operator if it is not responsible for deriving new tuples, or if a changeset contains only modified tuples and no dependencies have been updated.
Both push- and pull-models are used to flow data. When an edge connects operators that work with the same data (e.g. a pipeline of data transformations for the same data source) then changesets are pushed along the edge. When an edge connects operators with external dependencies such as other data sources, signals, or scale functions then these edges are flagged as reflow changesets. External dependencies are connected to Collector nodes along these reflow changeset edges. Collectors propagate tuples forward to their dependents, which then request (pull) the latest versions of their dependencies from the scheduler.
To support streaming nested data structures, operators can dynamically restructure the graph at runtime by extending newbranches, or pruning existing ones, based on observed data. These dataflow branches model their corresponding hierarchies as standard relations, thereby enabling subsequent operators to remain agnostic to higher-level structure. For example, a Facet operator partitions tuples by key fields; each partiion then propagates down a unique, dynamically-constructed dataflow branch, which can include other operators such as Filter or Sort. In order to maintain interactive performance, new branches are queued for evaluation as part of the same propagation in which they were created. To ensure changeset propagation continues to occur in topological order, operators are given a rank upon instantiation to uniquely identify their place in the ordering… The most common source of restructuring operations are scene graph operators, as building a nested scene graph is entirely data-driven.
Reactive Vega is open source and has been merged with the existing Vega project. It is available at http://vega.github.io/vega/, along with a live editor and a number of example interactive visualizations.
Note: I previously covered an earlier paper focusing on different aspects of Reactive Vega: “Declarative Interaction Design for Data Visualization.”
