GD-Wheel: A Cost-Aware Replacement Policy for Key-Value Stores – Li & Cox 2013
One of the wonderful things about reading papers and being exposed to lots of different problems and their solutions is that you never know when an idea might resurface and be useful in a new context or challenge you are facing.
Yesterday we saw how the team at Apache Kafka applied research from 1987 to design an efficient solution for tracking outstanding requests. This reminds us of an important (but often overlooked) principle: do the literature* search before diving into building a solution!. For any given problem, there is almost always an amazing number of very smart people who have looked in depth at the challenges involved and published their findings. You can save a lot of time and effort by understanding the lessons they have already learned and building on top of them. You can imagine how starting with the challenge of how best to manage a large set of expiring requests, you might find your way to the ‘Hierarchical Timing Wheels’ paper, even if you weren’t initially aware of that work before starting your search.
Suppose instead your challenge is to efficiently manage a cache eviction policy. There are no expiring timers or requests in sight. It seems much less likely your search would lead you to the Hierarchical Timing Wheels paper. Connecting the idea of hierarchical wheels to an application in cache eviction requires making a mental leap and seeing similarities that let you apply the idea in a new context. Of course, I have absolutely no idea how the connection was made in this particular instance, but it seems more likely to happen with prior exposure to the idea of hierarchical wheels. Many interesting new ideas emerge from joining the dots across different areas. These kinds of insights are much less likely to be available to you without a general curiousity habit that leads you to explore many different areas…
(*) Knowledge search might be a better term than literature search… asking people with expertise in the area is also a great strategy for example!
With all that said, let’s get stuck into today’s paper which examines cache eviction (replacement) policies that take into account not just how recently items have been accessed, but also how expensive it is to re-fetch / re-compute those items on a subsequent cache-miss.
Currently, key-value stores use LRU or an approximation to LRU as the replacement policy for choosing a key-value pair to be evicted from the store… However, neither LRU nor an LRU approximation is necessarily the best choice if the cost of recomputing cached values varies a lot. Then, it may be advantageous to take the cost of recomputation into account when making replacement decisions. In fact, real-world key-value store deployments and several representative web application benchmarks provide evidence that significant cost variations do exist.
The GD-Wheel replacement policy evaluated in the paper combines the Greedy-Dual algorithm with a variation on Hierarchical Timing Wheels that the authors call Hierarchical Cost Wheels. When integrated with memcached and evaluated using the Yahoo! Cloud Serving Benchmark, GD-Wheel shows big improvements over the default LRU-based replacement policy implementation in memcached:
This evaluation shows that GD-Wheel, when compared to LRU, greatly reduces the total recomputation cost as well as the average and 99th-percentile read access latency for the data. Specifically, the total recomputation cost is reduced by as much as 91.05%, and the average and 99th-percentile latencies are reduced by as much as 53.95% and 94.65%, respectively.
Before looking at the GD-Wheel algorithm, it’s reasonable to ask ‘is there really that much variation in recompute time for different items in the cache?’ Li & Cox discuss two different sources of cost variation: the first comes from storing different types of objects in the same cache, and the second comes from application variation within a given type.
An example of different types of objects in the same cache is Facebook’s use of memcached as both a database query results cache and as a generic computation cache for application-layer state. As an example of application variation amongst different requests at the same level, the authors cite a study of the RUBis and TPC-W benchmarks by Bouchenak et al. I’ve reproduced below a couple of the figures from that paper which illustrate this variation.
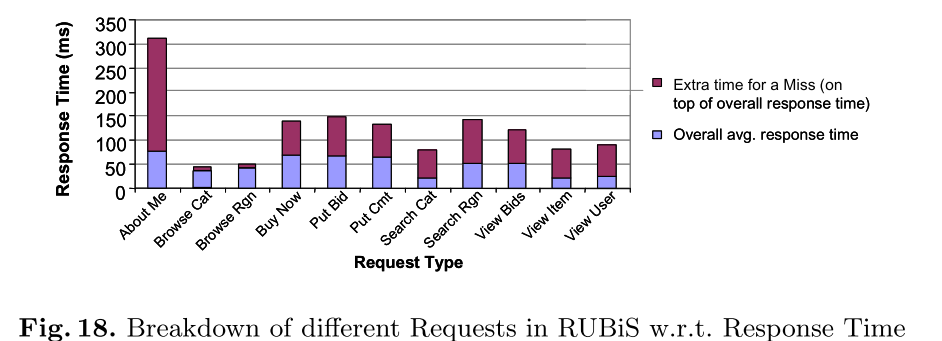
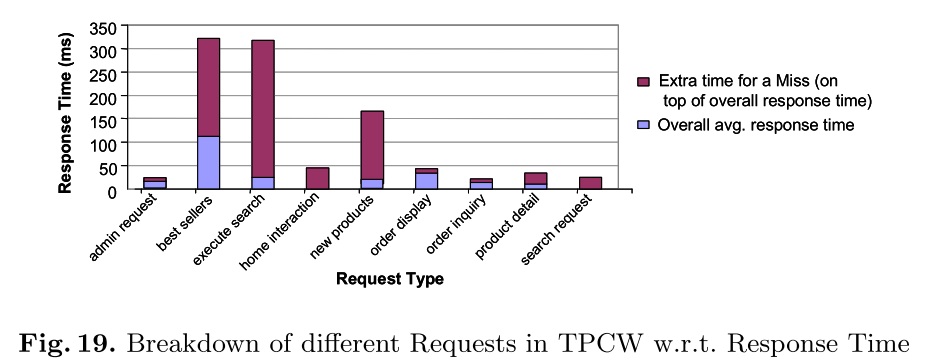
The foundation of GD-Wheel is the Greedy-Dual family of algorithms. In the best known implementation each item in the cache has an associated value H. The Higher an item’s H value, the more likely it is to stay in the cache. An inflation value L is used for ageing. The H value H(p) for an object p is set when p is first inserted into the cache and updated on every cache hit according to the formula
H(p) = L + c(p)
where c(p) is the cost of replacing p. L is initially set to 0. When it comes time to evict an object, L is set to the smallest H in the cache, and the object with H = L is evicted.
Just as H combines the cost and age inflation values, GreedyDual seamlessly integrates recency of access and cost of recomputation in making eviction decisions. Cao et al. implemented the GreedyDual algorithm by maintaining a priority queue based on the H values. Consequently, handling a hit or an eviction requires O(log n) time, which is slower than the LRU algorithm.
In Hierarchical Timing Wheels we saw that a priority queue of timers can be replaced by a timing wheel, and if there are more slots than can easily fit in a single timing wheel then we can use a hierarchy of timing wheels. This gives O(1) time.
In order to reduce the time complexity, we implemented the GreedyDual algorithm using a data structure that we call Hierarchical Cost Wheels. This data structure is inspired by Varghese and Lauck’s Hierarchical Timing Wheels. The Hierarchical Cost Wheels structure is made up of a series of Cost Wheels. A Cost Wheel is basically an array of queues. Instead of storing all objects in a single priority queue, key-value pairs with different costs are stored in different Cost Wheel queues. Since handling a key-value pair only needs to deal with a single queue inside the Hierarchical Cost Wheels, GD-Wheel requires only O(1) time for handling a hit or an eviction, just like LRU.
Each Cost Wheel has N slots. As before, we can arrange cost wheels in a hierarchy that acts somewhat like a base N number system. In the ‘units’ wheel, we find cache items with H values between 0 and (N-1). In the next wheel we find cache items with H values between N1 and L+(N2 -1), and so on (i.e., if N = 10 and L is still 0 we are looking at units, tens, hundreds, etc.).
The equivalent of PER-TICK BOOKKEEPING for timer wheels is per-eviction bookkeeping for cost wheels. An eviction happens when we need to add a new key-value pair p to the cache and it is already full. Selection of the pair to evict and update of L happens as described by the Greedy-Dual algorithm. The advancement of L is like the advancement of time for hierarchical timing wheels. When we complete one full revolution of a wheel, we advance the next higher wheel by one position and migrate cache entries that now find themselves in the zero’th slot to the next wheel down. The wheel at level m in the hierarchy will rotate one position each time L advances past a multiple of Nm.
On a cache-hit, an item’s H value is updated and it is dequeued from its current queue and enqueued again according to its new H value.
I don’t often like to do this, but here I have to point out that it seems to me the authors have made a mistake in their description of the use of hierarchical cost wheels: they advocate using wheels based on the absolute cost value – so the first wheel holds values 0..N-1, the second wheel holds values N..N2-1, and so on. But L is a monotonically increasing value, and so the minimum H value also monotonically increases. Given a long enough running program, you’re guaranteed to run out of wheels! Time (at least as modelled in Hierarchical Timing Wheels 😉 ) is a monotonically increasing value too. The solution there of course is that you don’t store timers based on the absolute time of expiry, but on the delta between the current time and the desired expiry time (the timer duration). We can do the same thing with hierarchical cost wheels and insert entries based on the delta between their H value and L. If L jumps up by multiple units as a result of an eviction, we simply process multiple ‘ticks’. Now we can happily run our cache in perpetuity! Also note that H(p) – L is simply cost(p)! So all we have to do is enqueue based on cost(p) to accommodate the cost component of GD, and let the turning of the wheels encapsulate the ageing component. It all falls out rather elegantly.
The experimental section shows that GD-Wheel performs well across a good cross-section of workloads:
This paper has argued that a key-value store’s replacement policy should take cost variations into consideration. Moreover, as a demonstration, it has introduced a new cost-aware replacement policy, GD-Wheel, which is an implementation of the GreedyDual algorithm with constant time complexity. In all of our experiments, GD-Wheel greatly reduced the total recomputation cost and improved the average application read access latency as compared to LRU. It also reduced the 99th percentile application read access latency which is critical in modern web applications.