Symmetry Reduction Enables Model Checking of More Complex Emerging Behaviours of Swarm Navigation Algorithms – Antuñya et al. 2015

Don’t let the title put you off – this paper is all about robot swarms!

Previously we looked at some nature-inspired optimisation algorithms, including Particle Swarm Optimisation which draws inspiration from the behaviour of flocks of birds. Today’s paper comes from the field of robotics, and it’s all about emulating some of nature’s behaviours by creating swarms of robots. Each individual robot follows simple rules, but taken together those simple rules, when applied in a swarm of robots, produce interesting emergent behaviours. It would be nice to know the robots we let loose will always behave as we wish…

There are some fun parallels to distributed systems too.

Robotic swarms consist of a set of robots with simple individual behaviour rules, working together in cooperation to achieve a more complex or emergent final behaviour. Appealing characteristics of swarms are the low cost incurred in producing the robots, which have a simple hardware design, scalability, and fault tolerance. Examples of their application to real-life tasks include nanorobotics, disaster rescue missions, and mining or agricultural foraging tasks.

Just as with concurrent and distributed systems, we have to worry about safety and liveness in this context. And as we’re releasing real machines out into the real world, we might want to verify those properties hold.

The emergent behaviours of a swarm of robots need to be verified, with respect to safety and liveness requirements, and validated to determine whether it is fit for purpose in the target environment. Safety requirements are the allowed behaviours of the system, and liveness requirements specify the dynamic behaviours expected to happen during the execution of the system.

Also in common with formal methods in distributed systems, state space explosion puts practical bounds on the complexity of systems that can be addressed. Letting the robots move around in continuous space (in modelling terms – they obviously do IRL) leads to an infinite state space. Instead we can chop space up into cells in a grid…

The discretization of the continuous space into cells of fixed size —i.e., a grid— is a solution that has been applied in swarms, to enable model checking. Even with the discretization of the environment into a “small” grid (e.g., 4×4 cells), the state-space explosion problem can occur due to the presence of other variables, which results in too many possible configurations of the robots in the grid.

Symmetry reduction techniques have been used to reduce state spaces in model checking. The authors show a way of encoding a swarm environment that eliminates symmetrically equivalent states from the state space – thus enabling formal verification to be applied to larger scale problems.

We implemented a relative encoding of a swarm environment model that eliminates symmetrically equivalent states from the state space. The swarm is assumed to be homogeneous; i.e., all the robots are considered identical in capabilities and rank. In the relative encoding, one robot is set as the “reference”, with a fixed location and direction of motion. The other robots’ locations and directions are defined based on this reference.

In an absolute encoding, if all the robots in a grid are simultaneously rotated in the same direction and shifted horizontally or vertically by the same distance, the robot’s new configurations change in location and direction. But with the relative encoding the locations and directions remain the same. This is the key to the state-space reduction.

In a grid of size m x m, and for robots that can travel in d different directions, the state space is reduced by a factor of dm²:

If a model with r robots in a m × m size grid (locations), with d possible directions, p other robots’ variables of domain sizes v_i, i = 1, …, p, and q global variables of domain sizes s_j , j = 1, …, q, is globally encoded, the size of the state space to be explored is (d × m² × v₁ × v₂ × … × v_p)^r × (s₁ × s₂ × … × s_q). In a relative encoding, the reference robot will have fixed location and direction, and the resulting state space will be of size (v₁ × v₂ × … × v_p) x (d × m² × v₁ × v₂ × … × v_p)^r-1 × (s₁ × s₂ × … × s_q). This corresponds to a reduction of the state space of d×m². In practice this bound changes according to the variables used in the relative encoding of an algorithm.

This also means that finding a counterexample in the relative model is equivalent to a class of counterexamples in the global model.

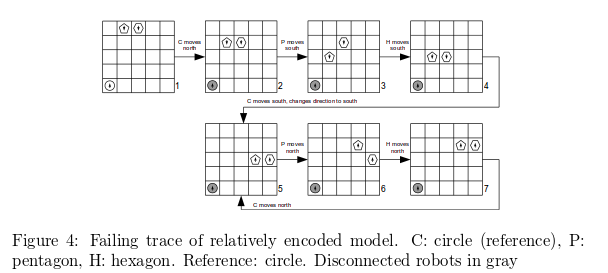
This approach is validated on the Alpha navigation algorithm, which rather disappointingly is known not to produce the desired behaviour!

The Alpha algorithm has been used as a case study to demonstrate how to verify emergent behaviours in swarms through model checking tools. In the Alpha algorithm, the robots in the swarm navigate the environment trying to maintain connectivity, defined as a wireless range. This is achieved by the
following rules: (a) the default movement of a robot is forward, maintaining its current direction. (b) When a robot loses connection with another robot, if the remaining number of connected robots is smaller than a value α, the robot makes a 180 degree turn. (c) Every time a robot regains connectivity with another, it performs a random turn.

The desired behaviour for a swarm is this case is that all robots shall eventually be connected. In prior work, a formal expression of the algorithm in Linear Temporal Logic showed this is false.

A global model and a relative model are both encoded for the NuSMV model checker. Both were able to show that the desired condition does not hold, but the relative model gives a much smaller state space (by about 2 orders of magnitude):

Thus, verification through model checking can be performed over larger grid sizes and higher numbers of robots, and also for more detailed abstractions that model navigation algorithms using more variables. Although the state space reduction is more significant in terms of the grid size, and not as expressive if considering realistic swarm sizes, analysing small robot groups can help to understand larger swarms within the lower limit bounds of swarm size, which demands more from the navigation algorithm.

Here’s an example of a counter-example found using the global encoding:

And this a more compact example found using the relative encoding: