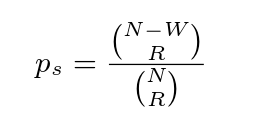Probabilistically Bounded Staleness for Practical Partial Quorums – Bailis et al. 2012, and Quantifying Eventual Consistency with PBS – Bailis et al. 2014

‘Probabilistically Bounded Staleness… ‘ was the original VLDB ’12 paper, and then the authors were invited to submit an extended version to the VLDB Journal (‘Quantifying Eventual Consistency…’) which was published in 2013/14. The journal paper changed some of the terminology used to model staleness (how out of date the data you see might be) to relate more strongly to earlier research in the space. I’m going to work mostly from the original 2012 edition here – as a standalone paper I find it more intuitive – and reference a few parts from the extended edition as needed.

Let’s start by unpacking the title a little.

Typically when using quorum replication we have N replicas; to write a value we send it to (wait for acknowledgements from) W of those replicas (a write quorum), and to read a value we consult R of the replicas (a read quorum) and return the most recent value from amongst the read quorum. The phrase quorum system is used to describe the set-of-sets from which the read and write quorums are chosen, and there is one quorum system per data item.

If you want strict (strong consistency) quorums you simply need to ensure that read and write replica sets overlap (for example, by ensuring each set contains a majority of the nodes). Partial quorums relax this constraint and allow sets of replicas that may not overlap (R+W ≤ N).

Quorum-replicated data stores such as Dynamo and its open source descendants Apache Cassandra, Basho Riak, and Project Voldemort offer a choice between two modes of operation: strict quorums with strong consistency or partial quorums with eventual consistency. Despite eventual consistency’s weak guarantees, operators frequently employ partial quorums —a controversial decision.

These stores all employ one quorum system per key, typically maintaining the mapping of keys to quorum systems using a consistent hashing scheme or a centralized membership protocol. Each node store multiple keys. “Dynamo denotes the replication factor of a key as N, the number of replica responses required for a successful read as R, and the number of replica acknowledgements required for a successful write as W.” From practitioner accounts, common quorum settings used in Practical Partial Quorums are as follows:

• Apache Cassandra defaults to N=3, R=1, W=1, and these settings appear to be widely used.
• Riak defaults to N=3, R=2, W=2, which users recommend for web, mission critical, and financial data. The configuration N=2, R=1, W=1 is recommended by some users for ‘low value’ data.
• Voldemort’s operators at LinkedIn often choose N=c, R=W=(c/2) for odd c. N=3, R=1, W=1 may be used for applications requiring very low latency and high availability, and N=2, R=1, W=1 is also used for some systems.

Are we making a deal with the devil here? We know we should achieve lower latency and higher availability with partial quorums, but at what cost? Let’s assume we’re going to get back a value that we wrote – but how out of date might that value be? What are the chances of a stale read? Until this paper, we didn’t really know how to answer that question (which also means that barring trial and error, we didn’t really have any way of figuring out appropriate values for N, R, and W). Intuitively, we can see that the greater the chance of overlap between read and write sets, the higher the probability that we’ll see a fresh data value. So although we can’t put absolute bounds on the behaviour of the system, we can give some probabilistic bounds – hence ‘Probabilistically Bounded Staleness‘ (PBS).

Thus: “Probabilistically Bounded Staleness for Practical Partial Quorums.”

Given N nodes, R members in a read quorum, and W members in a write quorum, we can calculate the probability that a read contains the most recently committed write. From N nodes we can form ‘take R from N’ combinations of read quorums in total. The subset of those that don’t include the latest value is all of the combinations excluding members of W, there are ‘take R from N-W’ combinations of them. The probability of a stale read is therefore:

This gives us the probability we’re reading the most recent value. We can generalise to the probability that the value we read is no more than k versions old (PBS k-staleness consistency – or (K, p)-regular semantics in the updated paper terminology) in a simple manner:

p_sk = p_s^k

We can also extend this notion to give the probability of monotonic reads – how likely is it that a client will see the same or newer version than a value it previously read? To work this out, we simply need to consider how many versions are likely to be written between client reads. This is a factor of the rate at which a client reads a data item, rate_cr, and the rate at which the global system writes to that data item, _rate_gw. Now we can treat this a special case of k-staleness consistency where k is given by 1 + (rate_cr/rate_gw):

p_{s M R} = p_s^{1 + (rate_cr/rate_gw)}

…quorums tolerating PBS k-staleness have asymptotically lower load than traditional probabilistic quorum systems (and, transitively, than strict quorum systems. … These results are intuitive: if we are willing to tolerate multiple versions of staleness, we need to contact fewer replicas. Staleness tolerance lowers the load of a quorum system, subsequently increasing its capacity.

These are very neat and simple models, but perhaps not as useful as they could be. There are two important factors to consider: firstly, it seems more natural to talk about staleness in the context of time, and secondly, we need to consider the anti-entropy mechanisms used by practical partial quorum systems.

Knowing that you’ll read a value no older than say 500ms, with some probability p, seems a more useful metric than a guarantee that you’ll see a value no older than k versions back. If the data item is only updated once every six months, that could be a very old value indeed! Of course, if we know the rate of updates then we can convert from k-staleness probability to a time-based probability.

But now we need to consider anti-entropy… once a write quorum has acknowledged a write, the system can proceed, but in the background the write continues to propagate to other replicas via some scheme. For example, we might send a write request to all N replicas, and return to the client as soon as we have W acknowledgements. This leads us to a time-based consistency metric:

PBS t-visibility models the probability of inconsistency for expanding quorums. t-visibility is the probability that a read operation, starting t seconds after a write commits, will observe the latest value of a data item. This t captures the expected length of the “window of inconsistency.”

The WARS model can help us to think about this; each letter represents a probability distribution for the time it takes messages to flow in the system:

• W models the distribution of message delays for a Write request making its way to replicas (note, this W is therefore different to the W writers in a quorum set)
• A models the distribution of message delays for Acknowledgements of those requests making their way back to the originator
• R models the distribution of message delays for a Read request making its way to replicas
• S models the distribution of message delays for read reSponse messages making their way back to the requester

A read coordinator will see a stale value if the first R responses received came from replicas that had not yet received the latest version (delayed by W)….

Writes have time to propagate to additional replicas both while the coordinator waits for all required acknowledgements (A) and as replicas wait for read requests (R). Read responses are further delayed in transit (S) back to the read coordinator, inducing further possibility of reordering. Qualitatively, longer write tails ( W ) and faster reads increase the chance of staleness due to reordering.

There is no nice closed-form equation we can use to model this though, so the authors turn to simulation:

Dynamo is straightforward to reason about and program but is difficult to analyze in a simple closed form….We instead explore WARS using Monte Carlo methods, which are straightforward to understand and implement.

A version of Cassandra was instrumented to profile WARS latencies and experiments showed that the model predictions and empirical observed values matched closely. The WARS model was then calibrated using latency data from LinkedIn and Yammer production systems to run a number of simulations. The full WARS algorithm can be found in the extended journal edition of the paper.

The model sheds light on the importance of write latency (in the tail):

The WARS model of Dynamo-style systems dictates that high one-way write variance ( W ) increases staleness. To quantify these effects, we swept a range of exponentially distributed write distributions (changing parameter λ, which dictates the mean and tail of the distribution) while fixing A=R=S… Our results confirm this relationship. As the variance and mean increase, so does the probability of inconsistency. Under distributions with fixed means and variable variances (uniform, normal), we observe that the mean of W is less important than its variance if W is strictly greater than A=R=S. Decreasing the mean and variance of W improves the probability of consistent reads. This means that, as we will see, techniques that lower one-way write latency result in lower t-visibility.

This effect is observed in the LinkedIn simulations using distributions calibrated from both disk and ssds:

LNKD-SSD and LNKD-DISK demonstrate the importance of write latency in practice. Immediately after write commit, LNKD-SSD had a 97.4% probability of consistent reads, reaching over a 99.999% probability of consistent reads after five milliseconds. … In contrast, under LNKD-DISK, writes take much longer (median 1.50ms) and have a longer tail (99.9th percentile 10.47 ms). LNKD-DISK’s t-visibility reflects this difference: immediately after write commit, LNKD-DISK had only a 43.9% probability of consistent reads and, ten ms later, only a 92.5% probability. This suggests that SSDs may greatly improve consistency due to reduced write variance.

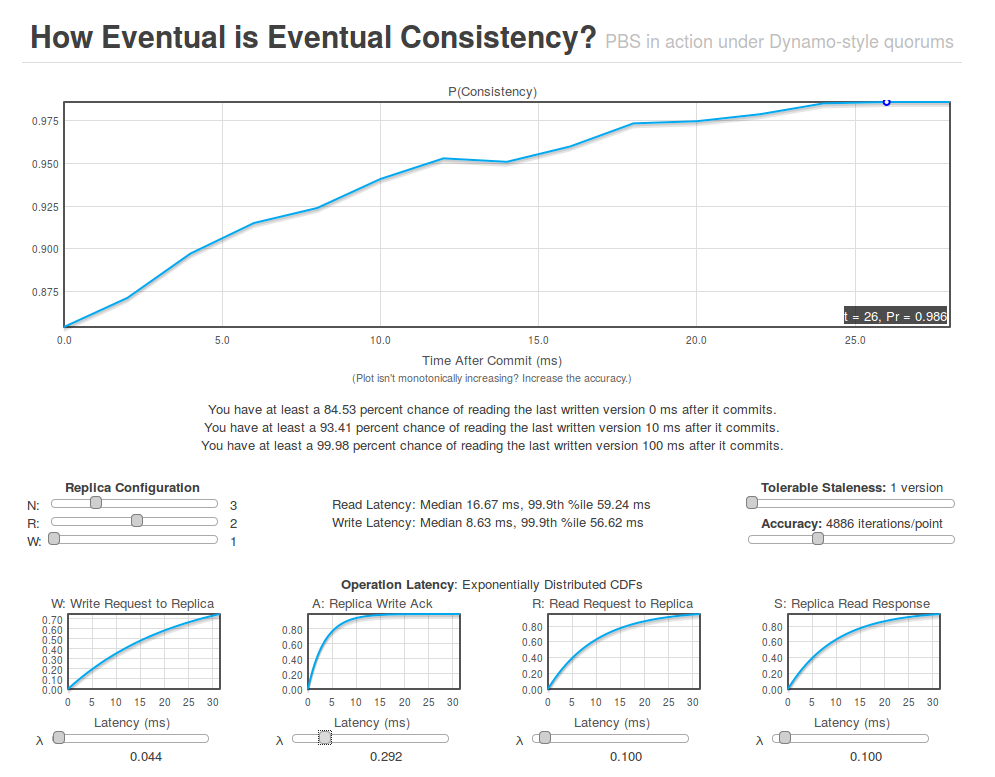
If we hold R=W=1, and increase the number of replicas (N), then we can see that the probability of consistency immediately after a write decreases as N increases.

Choosing a value for R and W is a trade-off between operation latency and t-visibility. To measure the obtainable latency gains, we compared t-visibility required for a 99.9% probability of consistent reads to the 99.9th percentile read and write latencies. Partial quorums often exhibit favorable latency-consistency trade-offs (Table 4). For YMMR, R=W=1 results in low latency reads and writes (16.4ms) but high t-visibility (1364ms). However, setting R=2 and W=1 reduces t-visibility to 202ms and the combined read and write latencies are 81.1% (186.7ms) lower than the fastest strict quorum(W=1, R=3).

We can disentangle replication for reasons of durability from replication for reasons of low latency and higher capacity. “For example, operators can specify a minimum replication factor for durability and availability but can also automatically increase N, decreasing tail latency for fixed R and W.”

Section 7 of the extended paper contains an interesting application of PBS to multi-key transactions and to causal consistency.

Transactional atomicity (not to be confused with linearizability, often called atomicity in a distributed context) ensures that either all effects of a transaction are seen, or none are. We can use PBS to provide conservative bounds on the probability of transactional atomicity. If we assume that each write operation in the transaction is independent and all writes are buffered until transaction commit, then the probability that we observe transactional atomicity is equal to P(all updates are visible)+P(no updates are visible).

Using the LinkedIn-Disk calibrated model, a transaction of size 2 has a 99.4% chance of consistency after 50ms, whereas a transaction of size 100 only has a 90.2% chance – this rises to 99.8% after 1s though.

Causal consistency has received considerable attention in recent research on distributed data stores. Under causal consistency, reads obey a partial order of versions across data items [7]. As an example, a social networking site might wish to enforce that comment replies are seen only along with their parents and would accordingly order replies after their parent comment in the partial order. We can use PBS to determine the likelihood of violating causal consistency in an eventually consistent data store.

The model as calibrated for LinkedIn and Yammer showed that…

Especially as the window of inconsistency closes within hundreds of milliseconds while the majority of requests for a data item often occur much later, we expect causal violations due to eventually consistent store operation to be rare during normal operation in practice.

(Though ignore the ‘during normal operation’ part of that at your peril 😉 ).

Of course, a probabilistic expectation is not a deterministic guarantee, but this data, paired with our PBS results, helps further illuminate how, for many services—particularly those with human-generated causal event chains (which are limited in inter-arrival time by both human processing time and fine motor reactions)—eventually consistent configurations often provide causal consistency.

The icing on the cake is that the team built an online simulator so that you can play with PBS for yourself calibrating WARS and setting N, R, and W to see the results. It’s a very engaging way to bring the model to life and a useful tool for understanding the likely behaviour of your systems.

I feel like there must be some interesting combination of the PBS Simulator and SimianViz (formerly Spigo) waiting to be put together!