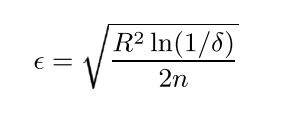Mining High-Speed Data Streams – Domingos & Hulten 2000

This paper won a ‘test of time’ award at KDD’15 as an ‘outstanding paper from a past KDD Conference beyond the last decade that has had an important impact on the data mining community.’

Here’s what the test-of-time committee have to say about it:

This paper proposes a decision tree learner for data streams, the Hoeffding Tree algorithm, which comes with the guarantee that the learned decision tree is asymptotically nearly identical to that of a non-incremental learner using infinitely many examples. This work constitutes a significant step in developing methodology suitable for modern ‘big data’ challenges and has initiated a lot of follow-up research. The Hoeffding Tree algorithm has been covered in various textbooks and is available in several public domain tools, including the WEKA Data Mining platform.

The goal is to create a knowledge discovery system that can cope with large volumes of data (perhaps an unbounded stream) without needing to fit everything in memory (40MB was the allotted amount used in their evaluation tests – remember this was 2000).

Ideally, we would like to have KDD systems that operate continuously and indefinitely, incorporating examples as they arrive, and never losing potentially valuable information. Such desiderata are fulfilled by incremental learning methods (also known as online, successive or sequential methods), on which a substantial literature exists. However, the available algorithms of this type have significant shortcomings from the KDD point of view. Some are reasonably efficient, but do not guarantee that the model learned will be similar to the one obtained by learning on the same data in batch mode. They are highly sensitive to example ordering, potentially never recovering from an unfavorable set of early examples. Others produce the same model as the batch version, but at a high cost in efficiency, often to the point of being slower than the batch algorithm.

Based on a statistical result known as the Hoeffding bound, the authors show how to create Hoeffding (decision) trees and build a Very Fast Decision Tree (VFDT) system based on them.

A key property of the Hoeffding tree algorithm is that it is possible to guarantee under realistic assumptions that the trees it produces are asymptotically arbitrarily close to the ones produced by a batch learner (i.e., a learner that uses all the examples to choose a test at each node). In other words, the incremental nature of the Hoeffding tree algorithm does not significantly affect the quality of the trees it produces.

In a classification problem, a set of N training examples of the form (x⃗,y) is given, where y is a discrete class label and x⃗ is a vector of d attributes. From these examples we need to produce a model y = f(x⃗) that will predict the class of future examples x⃗ with high accuracy. Decision tree learners create models in the form of decision trees, where each node contains a test on an attribute, each branch corresponds to a possible outcome of the test, and each leaf contains a class prediction. To learn a decision tree you recursively replace leaves by test nodes, starting at the root.

Our goal is to design a decision tree learner for extremely large (potentially infinite) datasets. This learner should require each example to be read at most once, and only a small constant time to process it. This will make it possible to directly mine online data sources (i.e., without ever storing the examples), and to build potentially very complex trees with acceptable computational cost.

In Hoeffding trees, in order to find the best attribute to test at a given node, only a small subset of the training examples that pass through that node are used. The key of course, is to determine how small that subset can be, and what guarantees we can give concerning it.

Thus, given a stream of examples, the first ones will be used to choose the root test; once the root attribute is chosen, the succeeding examples will be passed down to the corresponding leaves and used to choose the appropriate attributes there, and so on recursively. We solve the difficult problem of deciding exactly how many examples are necessary at each node by using a statistical result known as the Hoeffding bound (or additive Chernoff bound).

Given a real-valued random variable r with range R (e.g. 0-1 for a probability), and n independent observations of the variable, we can compute the mean of those observations, r̄. The Hoeffding bound tells us that with probability 1 – δ, the true mean of the variable is at least r̄ – ε, where:

The Hoeffding bound has the very attractive property that it is independent of the probability distribution generating the observations. The price of this generality is that the bound is more conservative than distribution-dependent ones (i.e., it will take more observations to reach the same δ and ε).

If G(X_i) is the heuristic used to choose test attributes, then we want to ensure with high probability the attribute chosen using n examples (where n is as small as possible) is the same that would be chosen using infinite examples. Suppose that we’ve seen n examples so far, and the best attribute predicted by G is X_a and the second best is X_b. Call the difference between the observed heuristic values of X_a and X_b ΔḠ

Now, given a desired δ, the Hoeffding bound tells us that X_a is the correct choice with probability 1 – δ if n examples have been seen at this node and ΔḠ > ε².

Thus a node needs to accumulate examples from the streamuntil ε becomes smaller than ∆G. (Notice that ε is a monotonically decreasing function of n.) At this point the node can be split using the current best attribute, and succeeding examples will be passed to the new leaves.

Pseudo-code for a Hoeffding tree algorithm based on this is given in table 1 of the paper.

The VFDT system was built using this algorithm, and included a number of additional optimisations:

• When two or more attributes have very similar scores, lots of examples may be needed to decide between them with confidence. But if they are very similar, it probably doesn’t matter too much which one we choose, so let’s just pick one after we reach some user-defined threshold and move on…
• We don’t need to recompute G after every example since it is unlikely the decision to split will be made at that specific point. So we can micro-batch and accept a minimum number of new examples before recomputing G.
• Under memory pressure, VFDT deactivates the least promising leaves in order to make room for new ones.
• Likewise VFDT can also drop early on attributes that do not look promising.
• VFDT can be initialised with a tree produced offline by a traditional batch learner. (Trained on a subset of the overall data).
• VFDT can rescan previously seen examples if desired.

This option can be activated if either the data arrives slowly enough that there is time for it, or if the dataset is finite and small enough that it is feasible to scan it multiple times. This means that VFDT need never grow a smaller (and potentially less accurate) tree than other algorithms because of using each example only once.