Distributed Snapshots: Determining Global States of Distributed Systems – Chandy & Lamport 1985.

What state is your distributed system in? In the absence of a universal clock, is that even a well-formed question? And if you could take a distributed snapshot of system state, would that be useful?

Through an algorithm that has simply become known as the ‘Chandy-Lamport’ algorithm, Chandy & Lamport show us that it is indeed possible (dare I even say easy?) to take a distributed snapshot of a distributed system, and that this can be a very useful thing indeed.

This paper presents algorithms by which a process in a distributed system can determine a global state of the system during a computation. Processes in a distributed system communicate by sending and receiving messages. A process can record its own state and the messagesit sends and receives; it can record nothing else. To determine a global system state, a process p must enlist the cooperation of other processes that must record their own local states and send the recorded local states to p. All processes cannot record their local states at precisely the same instant unless they have access to a common clock. We assume that processes do not share clocks or memory…

Furthermore, we have to achieve this without pressing a magic ‘pause’ button or disrupting the in-flight work of the system in any way:

The global-state-detection algorithm is to be superimposed on the underlying computation: it must run concurrently with, but not alter, this underlying computation.

If we can take a snapshot of the state of a distributed system, then we can test that state with a predicate (y) – for example, “is the system deadlocked.”

Several distributed-system problems can be formulated as the general problem of devising an algorithm by which a process in a distributed system can determine whether a stable property y of the system holds…

A channel is a directed communication link between two processes. Channels between processes are assumed to be error-free, and to deliver messages in the order in which they were sent. Messages may be delayed, but not forever. Chandy and Lamport show us how to capture a consistent snapshot of the state of every process and channel. The channel state is captured at the receiving end of each direct link. Collecting all of the local state snapshots to from the global picture is left as an exercise for the reader:

The algorithm described so far allows each process to record its state and the states of incoming channels. The recorded process and channel states must be collected and assembled to form the recorded global state. We shall not describe algorithms for collecting the recorded information because such algorithms have been described elsewhere. A simple algorithm for collecting information in a system whose topology is strongly connected is for each process to send the information it records along all outgoing channels, and for each process receiving information for the first time to copy it and propagate it along all of its outgoing channels. All the recorded information will then get to all the processesin finite time, allowing all processes to determine the recorded global state.

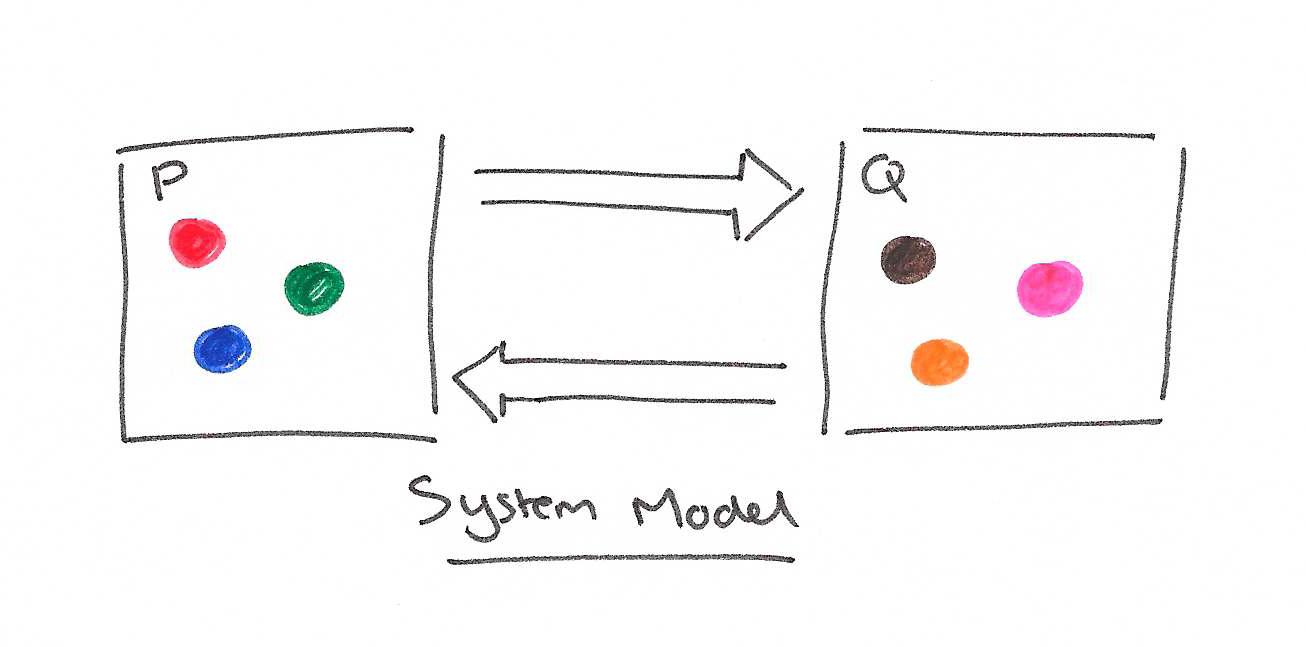
In a small twist on the examples given in the paper, imagine two processes exchanging a set of coloured balls between them (sending messages indicating transfer of ownership of a coloured ball). The state of each of the two processes (let’s call them P and Q) at any point in time is simply the set of balls in their possession. We’ll start the system in an initial state with the red, green and blue balls held by process P, and the brown, pink and orange balls held by process Q. We could represent this initial state as:

P(red, green, blue)
Q(brown, pink, orange) 

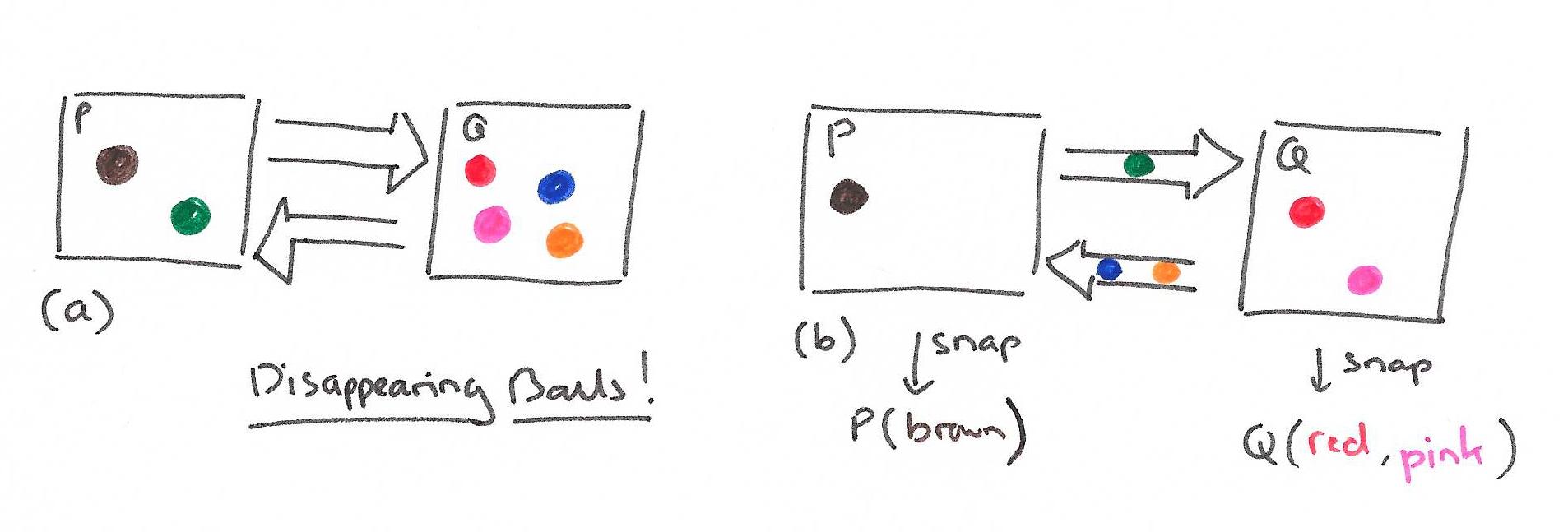
If we try to take system snapshots solely from the process perspective though, it turns out we can perform conjuring tricks – making balls appear out of, and disappear into, thin air. Ladies and Gentlemen, I now present to you the mystery of the disappearing balls:

Process P is in state P(brown, green) and process Q is in state Q(red, blue, pink, orange). Process P sends the green ball to process Q, and then snapshots its state: P(brown). Concurrently, process Q sends the blue and orange balls to process P, and snapshots its state – at this point in time Q has not yet processed the incoming green ball from P, so its snapshot state is Q(red, pink). To summarise, the snapshot state of the system is now:

P (brown)
Q (red, pink)

The green, blue, and orange balls have disappeared!

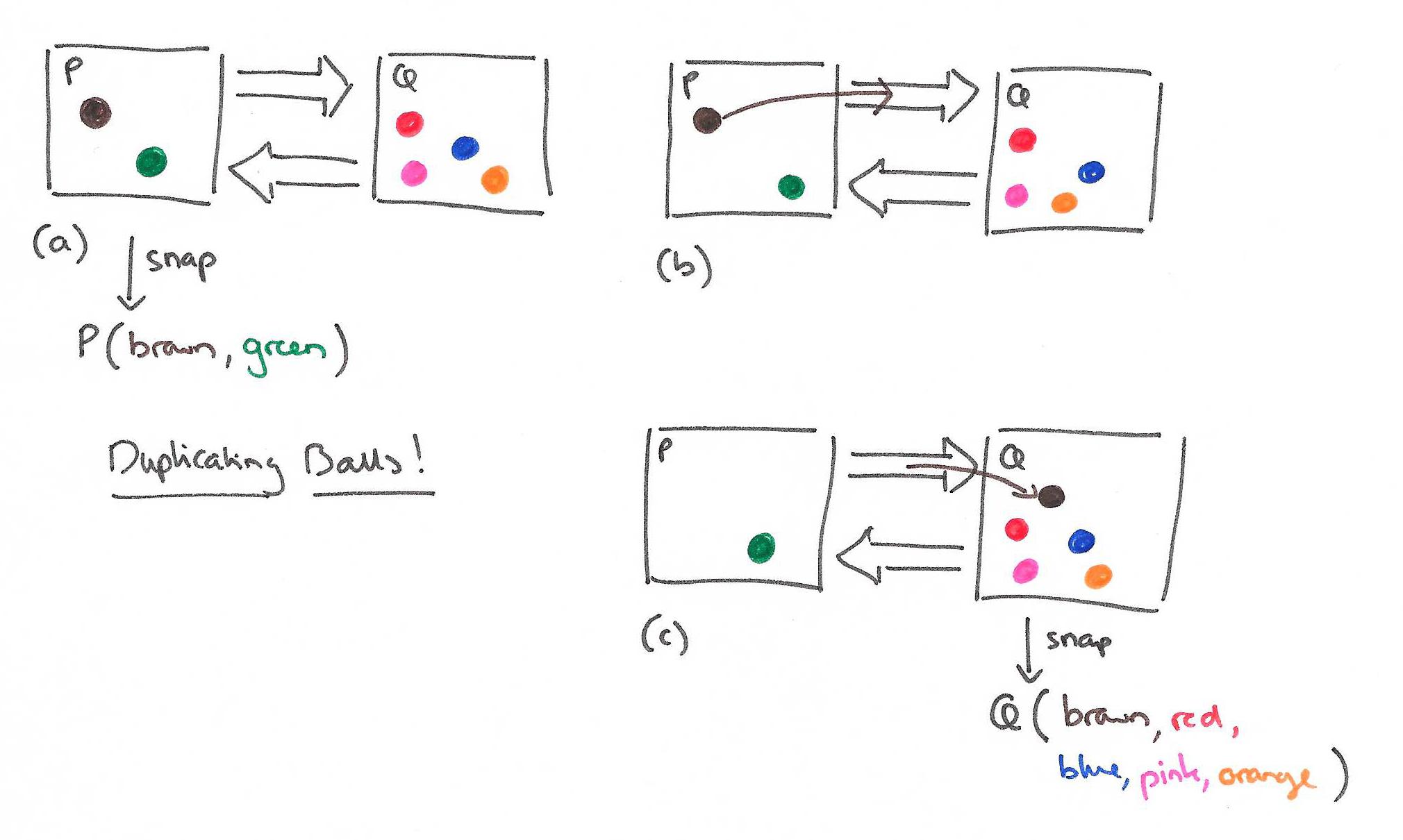
Fortunately, we’ve been able to recover our missing balls. Let’s take another snapshot with P starting out in state P(brown, green) and Q in state Q(red, blue, pink, orange) again. P snapshots its state, and then sends the brown ball to Q. Q processes the incoming message and then snapshops its state. So now we have a system state:

P(brown, green)
Q(brown, red, blue, pink, orange)

The brown ball is in two places at once! It’s like the opposite of quantum uncertainty – the ball is in one place at any one point in time, but as soon as we try to measure it, it appears in both places!

While these may be fun parlour tricks (we have a riot in the Colyer household 😉 ), I think you’ll agree they’re not terribly useful as snapshots of the system state as both examples clearly violate the simple system invariant that there is one each of the the brown, green, red, blue, pink, and orange balls. Of course, what we need to do is capture not just the state of the processes, but also the state of the channels. And we need to do this in a way that results in a consistent overall snapshot.

The solution is found in sending a marker along channels, which acts as a logical point in time. When P is asked to record its state, it does so and then immediately sends a marker message on each outbound channel from P. The full global state detection algorithm is captured by a Marker Sending Rule and a Marker Receiving Rule:

• The Marker Sending Rule for a process p: for each channel c incident on, and directed away from p, p sends one marker along c after p records its state and before p sends any further messages along c.
• The Marker Receiving Rule for a process q: on receiving a marker along a channel c, if q has not yet recorded its state then it records its state, and records the state of c as empty. However, if q has already recorded its state, then the state of c is simply recorded as the sequence of messages received along c inbetween q recording its state and receiving the marker on c.

To ensure that the global-state recording algorithm terminates in finite time, each process must ensure that (L1) no marker remains forever in an incident input channel and (L2) it records its state within finite time of initiation of the algorithm. The algorithm can be initiated by one or more processes,each of which records its state spontaneously, without receiving markers from other processes; we postpone discussion of what may cause a processto record its state spontaneously…. if the graph is strongly connected and at least one process spontaneously records its state, then all processes will record their states in finite time (provided L1 is ensured).

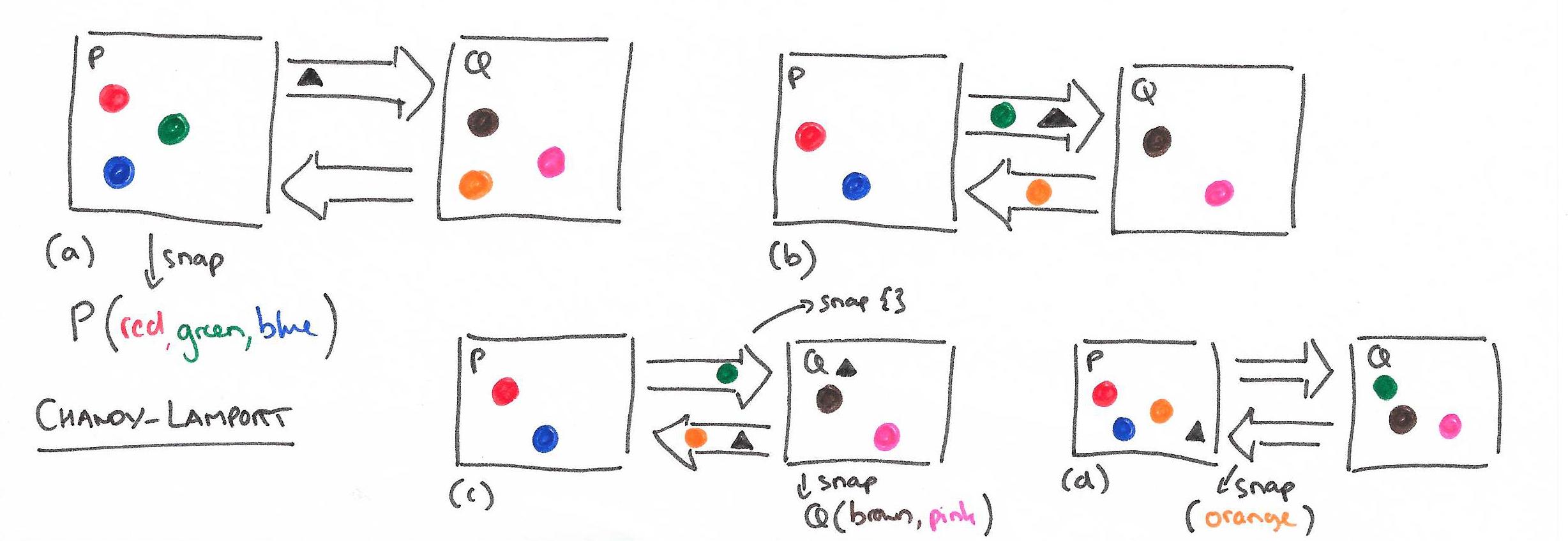
Let’s take a snapshot of our coloured ball system; starting in state P(red,green,blue), and Q(brown, pink, orange).

P snapshots its state as P(red, green, blue), puts a marker into channel PQ, and then continues processing by sending the green ball to Q along channel PQ. In parallel, Q has sent the orange ball to P, so Q is in state Q(brown, pink). Q receives the marker on channel PQ. When it receives the marker, Q snapshots its state – Q(brown, pink) – and records the state of channel PQ as empty. Q now sends a marker along channel QP. P receives the orange ball on channel QP, and then the marker. Since P has already recorded its state, it simply records the state of channel QP as (orange). The complete snapshot state is therefore:

P(red, green, blue)
channel PQ ()
Q(brown, pink)
channel QP (orange)

If you play around with a few variations, you should quickly be able to satisfy yourself that both missing and duplicate ball problems are prevented.

The global state recorded by the algorithm may not correspond exactly to any state the system was in at a given point in time, but it does provide a logically consistent snapshot of a state that is guaranteed to be reachable from the initial system state, and from which the final (terminal) system state is reachable.