Knowledge and Common Knowledge in a Distributed Environment – Halpern & Moses ’90 (initial version 1984).

This is the first of five ‘Desert island papers’ chosen by Peter Alvaro, and what a great choice to kick the week off with. It’s a long read, coming in at 36 pages (45 if you include the proofs in the appendices), but well worth studying. It’s also a great reminder of just how subtle some of the issues in distributed systems can be.

Reasoning about knowledge seems to play a fundamental role in distributed systems. Indeed, such reasoning is a central part of the informal intuitive arguments used in the design of distributed protocols. Communication in a distributed system can be viewed as the act of transforming the system’s state of knowledge. This paper presents a general framework for formalizing and reasoning about knowledge in distributed systems.

By explicitly reasoning about the states of knowledge of the components of a distributed system we gain insight into the basic structure and limitations of protocols in a given system. A crucial aspect of such protocols is the fact that a number of different processors cooperate in order to achieve a particular goal. “This often requires care in distinguishing subtle differences between seemingly similar states of knowledge.”

Two running examples are used to motivate the discussions in the paper: the muddy children puzzle, and the two generals (coordinated attack) problem. You probably know about the two generals, the muddy children puzzle is less well-known:

Imagine n children playing together… during their play some of the children, say k of them, get mud on their foreheads. No one says a thing. Along comes the father, who says “At least one of you has mud on your head,” thus expressing a fact know to each of them before he spoke (if k > 1). The father then asks the following question over and over: “Can any of you prove you have mud on your head?” Assuming that all the children are perceptive, intelligent, truthful, and that they answer simultaneously, what will happen?

Spoiler alert: the first k-1 times the father asks the question they all say “no”, but on the kth time the dirty children will answer “yes.” And it further turns out that ‘by announcing something that the children all know, the father somehow manages to give the children useful information! How can this be?’

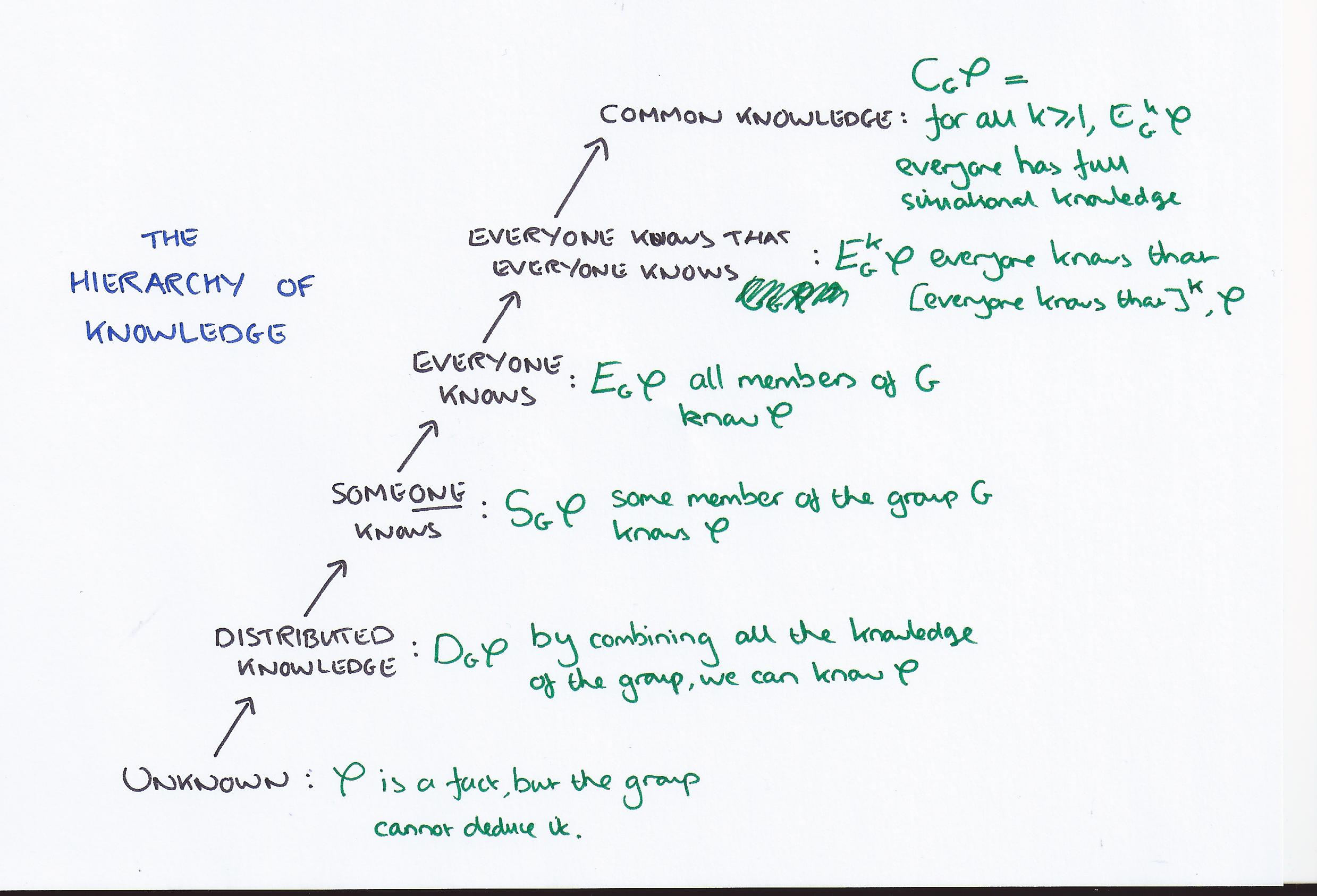
The answer, and the basis for reasoning about knowledge in distributed systems comes from a hierarchy of group knowledge that Halpern and Moses define.

You can climb up the hierarchy of knowledge all the way from a true fact F that the group does not know, to common knowledge which as defined is quite a strong condition: “everyone knows that, everyone knows that, …. everyone knows F” (for as many levels of ‘everyone knows that’ as you like). Using this framework the authors manage to make it quite clear exactly what is going on when the father tells the children something they all know, and yet it makes a difference overall. In ascending order, the knowledge states are:

• unknown – F is a fact but the group don’t know it.
• distributed knowledge – if you combine all of the knowledge from every member of the group, you can deduce F.
• someone knows – some member of the group knows F.
• everyone knows – all members of the group know F.
• (everyone knows)^k – everyone knows that everyone knows that … F, for k levels of ‘everyone knows’.
• common knowledge – for all k >= 1, (everyone knows)^k F.

…in such a system, every two levels in the hierarchy can be separated by an actual task, in the sense that there will be an action for which one level in the hierarchy will suffice, but no lower level will.

And the effect of that father’s statement? It took the group from everyone knows to common knowledge.

Using the hierarchy of knowledge to reason about protocols

We feel that understanding the role knowledge plays in problems such as coordinate attack is a first step towards simplifying the task of designing and proving the correctness of protocols.

The authors go on to describe a general model of a distributed system based on ‘runs’ (‘traces’ is a term you may be more familiar with).

We shall often be interested in the set of runs generated by running a particular protocol, under some assumptions of the communication medium. Intuitively, a protocol is a function specifying what actions a processor takes (which in our case amounts to what messages it sends) at any given point (after the processor wakes up) as a function of the processor’s local state.

And a processor’s local state is in turn simply determined by its history… There follows a formalism for group knowledge based on this underlying general model. The authors quickly introduce and then build upon new concepts, so it takes some effort to follow along. The model put forward is shown to agree with the ‘well-known modal logic of S5.’ (I had to look that up!). Fortunately we can still follow the consequences that fall out from the model.

Firstly, common knowledge seems to require some very special powers:

This lemma shows that common knowledge requires simultaneity in a very strong sense: When a new fact becomes common knowledge in a group G, the local histories of all of the members of G must change simultaneously to reflect the event of the fact’s becoming common knowledge.

Which might be a problem because:

Any correct protocol for the coordinated attack problem has the property that whenever the generals attack, it is common knowledge that they are attacking.

‘Theorem 5’ finishes us off: nothing can become common knowledge unless it is also common knowledge in the absence of communication.

Hence it turns out that:

Any correct protocol for the coordinated attack problem guarantees that neither party ever attacks.

In real life though, generals do manage to attack every now and then. How come?

It seems that in real life generals do not need a protocol that guarantees such a strong condition, and can probably make do with one that guarantees a non-simultaneous attack. We may want to weaken this requirement in order to get something that is achievable…

One way out is to introduce probability: a protocol that guarantees if one party attacks then with high probability the other will attack is achievable, under appropriate probabilistic assumptions about message delivery.

Common knowledge is not attainable in a system in which communication is not guaranteed, nor is it attainable if communication is guaranteed, but there is no bound on message delivery times. All practical distributed systems have some inherent temporal uncertainty – but if we can bound it, we can do better.

Suppose there is a bound, epsilon, such that all processors receive a message with epsilon time units of it being sent. Then epsilon-common knowledge is achievable.

We are thus in a state of knowledge that is analogous to common knowledge; here however, rather than everyone knowing F at the same instant, they all come to know F within an interval of epsilon time units. We call this state of group knowledge epsilon-common knowledge.

What is communication is not synchronous, but asynchronous (yet still guarantees that every message will eventually reach every processor)?

This situation, where it is common knowledge that if m is sent then everyone will eventually know that m has been sent, gives rise to a weak state of group knowledge which we call eventual common knowledge.

This eventual knowledge turns out not to be good enough for our generals though:

In the coordinated attack problem, any protocol that guarantees that whenever either party attacks the other party will eventually attack, is a protocol in which necessarily neither party attacks.

Thus: “asynchronous communication channels are of no use for coordinating actions that are guaranteed to be performed at all sites within a predetermined fixed time bound.”

You may be familiar with the device of introducing clocks to break the logjam. Relativistic notions of time are sufficient. Timestamped knowledge represents the fact that some processor knows a fact at some time T by its local clock.

In many distributed systems timestamped common knowledge seems to be a more appropriate notion to reason about than ‘true’ common knowledge. Although common knowledge cannot be attained in practical systems, timestamped common knowledge is attainable in many cases of interest and seems to correspond closely to the relevant phenomena with which protocol designers are confronted.

In conclusion…

We have shown that reasoning about the knowledge of a group and its evolution can reveal subtleties that may not not otherwise be apparent, can sharpen our understanding of basic issues, and can improve the high-level reasoning required in the design and analysis of distributed protocols and plans.