TLA+ model checking made symbolic Konnov et al., OOPSLA’19
TLA+ is a formal specification language (Temporal Logic of Actions) particularly well suited to reasoning about distributed algorithms. In addition to the specification language, the TLA+ toolset includes a model checker (TLC) and a theorem prover (TLAPS).
Given the huge state spaces involved in many real-world settings, the TLC model checker can take a long time / a lot of resources to run.
While progress towards proof automation in TLAPS has been made in the last years, writing interactive proofs is still a demanding task. Hence, the users prefer to run TLC for days, rather than writing proofs.
Like many people (?!), I often find myself wishing I had the time (and skills!) to model some of the algorithms in the papers I read and taken them for a spin in a checker. So anything that can help make that a little bit more tractable is interesting to me.
This paper introduces an alternative symbolic model checker for TLA+ called APALACHE:
Unlike TLC, APALACHE translates the underlying transition relation into quantifier-free SMT constraints, which allows us to exploit the power of SMT solvers.
The implementation uses the Z3 SMT solver. APALACHE can be used to check inductive invariants and bounded safety properties. A TLA+ inductive invariant is a state formula expressing what must be true about the system state after every algorithm step. (It’s called inductive because you show that the invariant holds for the initial state, Init, and after every step transition from a state where it holds).
After invariance, the next most common safety property of a TLA+ specification that one proves is that it implements a higher-level specification under a refinement mapping. – “Proving Safety Properties,” Lamport’19, p36.
Given a safety property 
The testbed for APALACHE (pitted against TLC) is a collection of examples from the TLA+ Examples project on GitHub. Some of these examples have been hand-tuned to make them efficient for TLC to check, no such tuning is done for APALACHE.
The benefits of APALACHE show most clearly in checking inductive invariants. When the invariants hold, and TLC is fast, APALACHE is also fast. But when TLC starts to struggle (e.g., almost 3 hours on TwoPhase-7), APALACHE remains relatively fast (e.g. 4 seconds on this same benchmark).
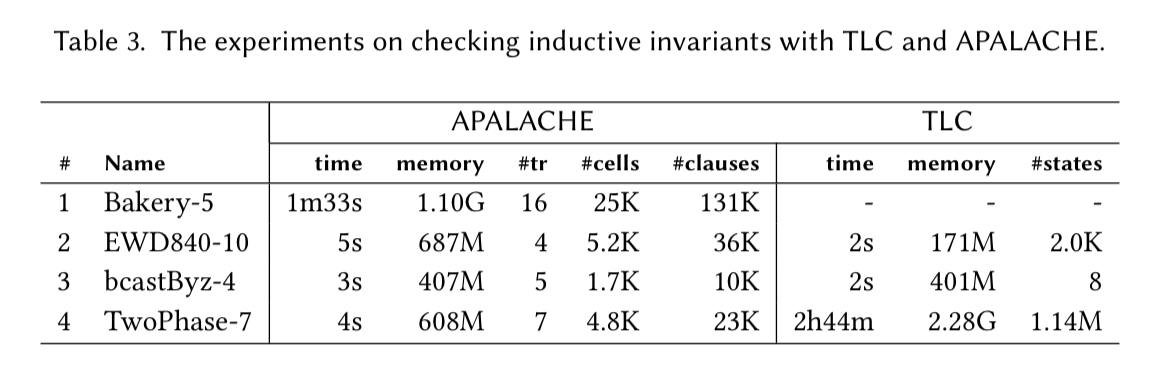
When the authors deliberately introduce an invariant violating change (e.g., removing a constraint, changing a constant, or introducing an arithmetic error) then APALACHE really shines. It finds the problem in a handful of seconds, whereas TLC sometimes times out after 23 hours. That’s going to make a big difference when you’re iterating towards correctness.
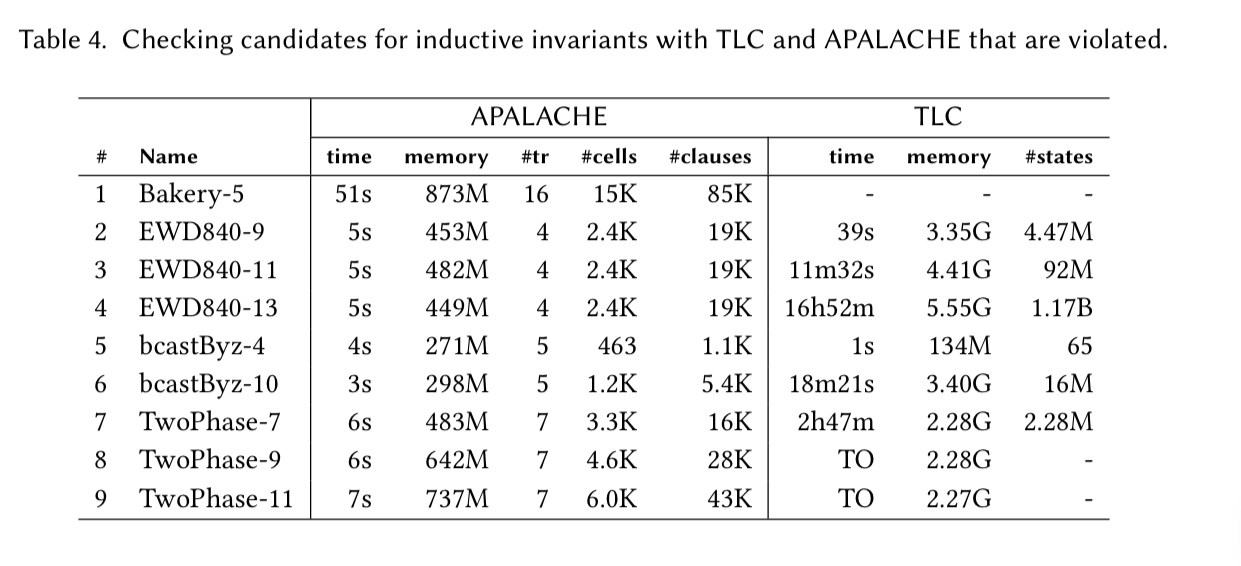
It’s not all good news though. First there is the general remark that both APALACHE and TLC struggle with the Paxos-like algorithms in the example set:
There are a number of Paxos-like algorithms. These are rather complex TLA+ specifications of real distributed algorithms. Both TLC and our tool get stuck after 10-15 steps. We only included the famous Paxos and Raft…
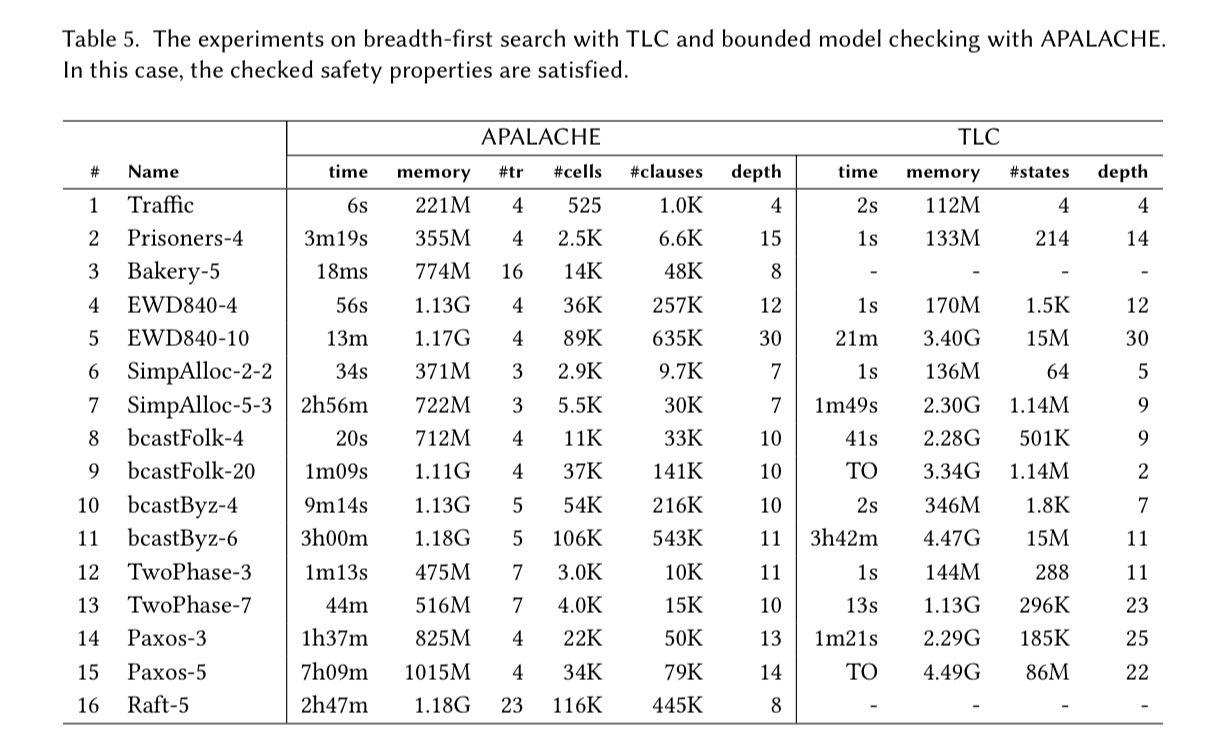
When we look at bounded model checking of safety properties, the scorecard is very mixed: sometimes APALACHE is faster than TLC, and sometimes it’s the other way round. APALACHE never times out though, which TLC does on a couple of the examples.
If we deliberately introduce a violation once more, then APALACHE is consistently quick in finding it again.
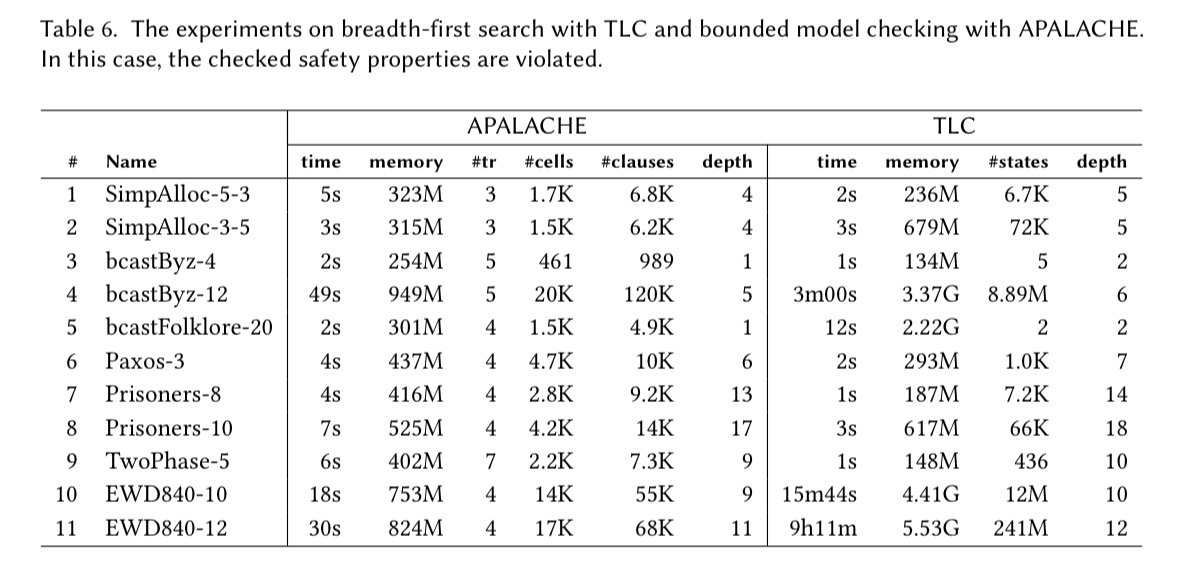
Our experiments show a clear advantage of APALACHE over TLC when checking inductive invariants, both in the satisfiable and unsatisfiable case. However, the advantages of our model checker are less pronounced when analyzing safety by bounded model checking. Over 20 years, TLC has collected clever heuristics for TLA+. We hope that with the growing number of users, specifications will get tuned to our model checker, as is now happening with TLC.
How APALACHE works under the covers
APALACHE shares two assumptions with TLC:
- All input parameters to a specification to be checked are fixed
- Reachable states and the values of parameters are finite structures.
The first stage in processing is to turn an (untyped) TLA+ specification into a collection of typed expressions. First TLA+ operators (a bit like macros) are inlined (flattened). Then TLA+ expressions relating state before and after a step (e.g. 
Developing a fully automatic type inference engine for TLA+ is a challenge on its own. In this paper, we follow a simple approach: in most cases, the types are computed automatically by propagation; when the tool fails to find a type, it asks the user to write a type annotation…. In practice, the user only has to give the types of empty sets, empty sequences, and records.
Converting the full richness of TLA+ expressions into SMT constraints would be a tough job. So APALACHE introduces an intermediate set of operators, KerA+, that can express all but a few TLA+ expressions. KerA+ is deliberately minimalistic – even basic operators such as the Boolean operators are omitted, since they can be expressed in terms of if-then-else.
Once the TLA+ expressions have been rewritten as KerA+ expressions, the final step is to turn those into an equisatisfiable quantifier-free SMT formula (i.e., something you can give to an SMT solver and get back an answer).
…we introduce an abstract reduction system that allows us to iteratively transform a KerA+ expression by applying reduction rules. The central idea of our approach to rewriting is to construct an overapproximation of the data structures with a graph whose edges connect values such as sets and their elements. We call this graph an arena, as it resembles the in-memory data structures that are created by the explicit-state model checker TLC.
Sections 5-10 in the paper give the details of this translation, section 11 demonstrates soundness. I suspect only a minority of The Morning Paper readers are interested in that level of detail, so I’ll refer those of you who want more to the full paper.
If you want to try APALACHE out for yourself, you’ll find the code on GitHub at konnov/apalache.