zkLedger: privacy-preserving auditing for distributed ledgers

zkLedger: privacy-preserving auditing for distributed ledgers Narula et al., NSDI’18

Somewhat similarly to Solidus that we looked at late last year, zkLedger (presumably this stands for zero-knowledge Ledger) provides transaction privacy for participants in a permissioned blockchain setting. zkLedger also has an extra trick up its sleeve: it provides rich and fully privacy-preserving auditing capabilities. Thus a number of financial institutions can collectively use a blockchain-based settlement ledger, and an auditor can measure properties such as financial leverage, asset illiquidity, counter-party risk exposures, and market concentration, either for the system as a whole, or for individual participants. It provides a cryptographically verified level of transparency that’s a step beyond anything we have today.

The goals of zkLedger are to hide the amounts, participants, and links between transactions while maintaining a verifiable transaction ledger, and for the Auditor to receive reliable answers to its queries. Specifically, zkLedger lets banks issue hidden transfer transactions which are still publicly verifiable by all other participants; every participant can confirm a transaction conserves assets and assets are only transferred with the spending bank’s authority.

Setting the stage

A zkLedger system comprises n banks and an auditor that verifies certain operational aspects of transactions performance by the basks. A depositor or set of depositors can also issue and withdraw assets from the system. Issuance and withdrawal of assets are global public events.

The main action takes place when banks exchange assets by creating transfer transactions. A transfer moves v shares of some asset t to a given recipient bank (or banks). Agreements to transfer are arranged outside of the system, and settled on zkLedger. All transactions are submitted to a globally-ordered append-only ledger, which could be a blockchain.

Cryptographic building blocks

To protect their privacy, banks do not broadcast payment details in the clear. Instead, banks post commitments to the ledger, using Pedersen commitments. Pedersen commitments are perfectly hiding and computationally binding, they are also additively homomorphic, a fact which zkLedger makes extensive use of. (By additively homomorphic we mean that given commitments to values v1 and v2, there is an operation we can perform on those commitments to produce a commitment to the value v1 + v2. )

Every bank has a Schnorr signature keypair and distributes their public key to all other system participants.

Assertions about payment details are made based on non-interactive zero-knowledge proofs (NIZKs). In an NIZK scheme a prover can convince a verifier of some property about private data the prover holds, without revealing the private data itself. The binary string proof $\pi$ can be appended to the ledger and verified by any party of the system without interaction between the prover and the verifier.

In theory, NIZK proof systems exist for all properties in NP whereas the practical feasibility of NIZKs is highly dependent on the complexity of the property at hand… The design of zkLedger is carefully structured so that all NIZK proofs have particularly efficient constructions.

The zkLedger

At a high level zkLedger looks like this:

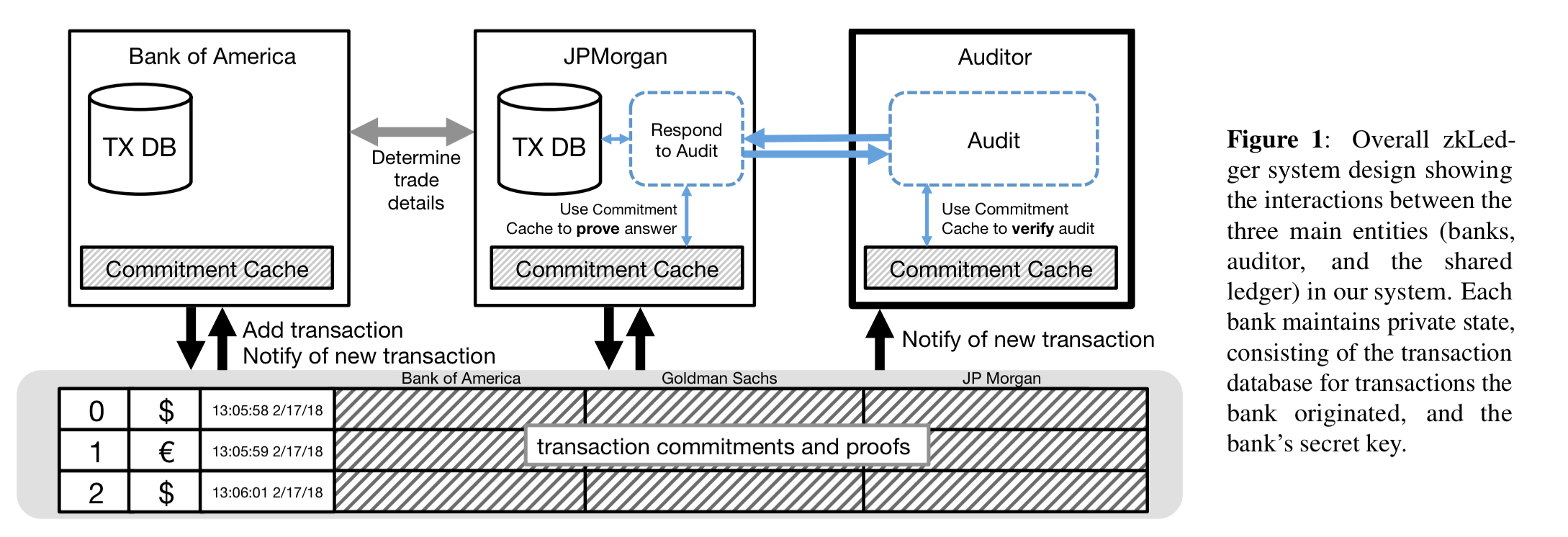
Banks maintain their own private state, and for efficiency a commitment cache which holds a rolling product of commitments by row and by asset so that it can quickly produce proofs and answer questions from auditors. The ledger itself has own entry (row) per transaction, and every row contains one column for each participating bank. (Banks can be added or removed by appending special signed transactions to the ledger).

Suppose bank A wants to transfer 100 shares of an asset to bank B. The transaction row conceptually contains a -100 entry in A’s column, 100 in B’s column, and zero in every other column. The values are not posted in the clear though, instead the column entries are Pedersen commitments for the respective amounts. Since there is no way for an outsider to tell the difference between a commitment to zero and any other value, both the transaction amounts and participants are protected.

Keeping values and participants private is a good start, but we also need to maintain overall integrity via the following invariants:

Transfer transactions cannot create or destroy assets
The spending bank must give consent to the transfer, and must own enough of the particular asset to execute the transaction

The first invariant is upheld via a proof of balance, and the second invariant is upheld using a proof of assets.

For proof of balance it suffices to show that the values in a given row sum to zero. If the the prover chooses the random inputs r to the commitments such that all of the r values also sum to zero, then a verifier can confirm that the the committed values all sum to zero by showing that the product of the commitments is 1.

A common approach to showing proof-of-assets is to use Unspent Transaction Objects (UTXOs). In a system that doesn’t use zk-SNARKs though, this leaks the transaction graph. zk-SNARKs require a trusted third party for setup, which zkLedger wants to avoid: “the consequences of incorrect or compromised setup are potentially disastrous…”

In zkLedger, a bank proves it has assets by creating a commitment to the sum of the value for the asset in its column, including this transaction. If the sum is greater than or equal to 0, then the bank has the assets to transfer. Note that this is true since the bank’s column represents all the assets it has received or spent, and the Pedersen commitments can be homomorphically added in columns as well as in rows.

In addition, in its own entry (where the value is negative), a bank includes proof of the knowledge of its secret key as a proof of authorisation. Thus we have a disjunctive proof – either the committed value for an entry is greater than or equal to zero, or the creator of the transaction knows the secret key for the entry.

There’s one more issue we still need to consider: commitments rely on modulus. If we’re using modulus N, we need to make sure that committed values are within 0..N-1. Range proofs are used to show that values are within range, and zkLedger supports asset value amounts up to a trillion. Now the only thing I can really tell you about range proofs is that they’re the most expensive part of generating the transaction and if we’re not careful we need two of them: one for the commitment value and one for the sum of assets in the column. With a level of indirection zkLedger manages to get this back down to just one range proof per transaction.

Auditing

The auditor can ask a query of a Bank, such as “How many Euros did you hold at time t?,” and the bank responds with an answer and a proof that the answer is consistent with the transactions on the ledger. The auditor can multiply commitments in the bank’s column for Euros, and verify the proof and answer with the total. Given the table construction, the auditor knows that they are seeing every asset transfer – there is no way for a bank to ‘hide’ assets on the ledger.

Given that every bank is affected by every transaction (because each row contains a commitment for every bank, even if to the value zero), each bank needs to be able to total and prove all of the commitments in its column. To do this, the bank needs to know the random input used for each of those commitments, otherwise it won’t be able to open up commitments to the auditor. To meet this requirement, the spending bank is required to include a publicly verifiable Token in every entry, which is based on a combination of the bank’s public key and the random input. The token construction enables the bank to show that the asset total is correct without actually needing to know the random input (details in §4.2 of the paper). Alongside the token, we also need a proof of consistency that the same random input was used both in construction of the token and in forming the value commitment.

Through the use of sums, means, ratios, variance, co-variance, and standard deviation, an auditor in zkLedger can determine the following, among other measurements: leverage ratios (how much of an asset a bank has on its books compared to other holdings); concentration (using a measure called the Herfindahl-Hirschman Index – HHI – to measure how competitive an industry is); real-timet price indexes.

Sums are supported via the additive structure of Pedersen commitments. For everything else there is map/reduce. Take as an example an auditor that wants to calculate the mean transaction size for a given bank and asset. A commitment to the total value is obtained by summing the column, but we don’t know what the denominator should be, because we don’t know which entries are actually commitments to zero. Map/reduce solves this: in the map step the bank produces new commitments per row indicating whether or not the bank was involved in the transaction (1 if the bank is involved, zero otherwise). In the reduce step these commitments are summed and the result is sent to the auditor along with the corresponding proofs. More complex queries may require multiple map and reduce computations (see the example in §5 of the paper for computing variance).

Putting it all together

For a transfer transaction, each entry in the row contains:

A Pedersen commitment to the value being transferred
An audit token so that audit requests can be answered without knowing the random input to the commitment
A proof -of-balance
A proof-of-assets
A proof-of-consistency between tokens and commitments

Banks can also add additional metadata – either encrypted or in plaintext.

Performance evaluation

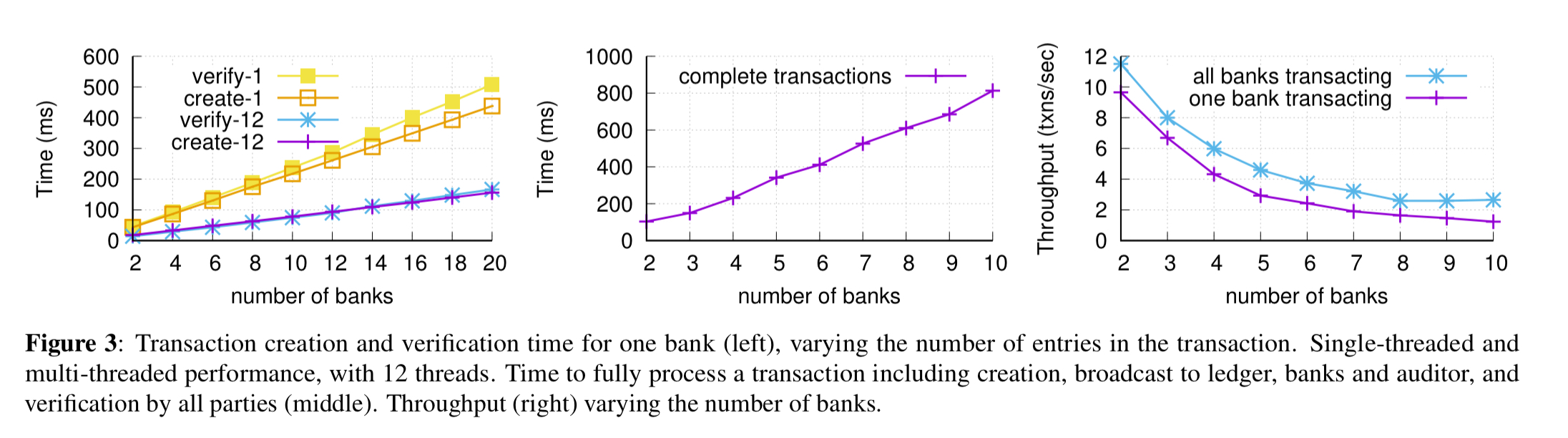
A Go prototype of zkLedger shows that it is possible to create the needed proofs in milliseconds.

However, the cost of verifying transactions increases quadratically with the number of banks, and all transactions must be strictly serialised. Banks can verify transaction in parallel, so the time to process transactions increases linearly.

(Enlarge)

With 10 banks, we’re already down to around 2 transactions per second. “We are optimistic that a faster range proof implementation will directly improve performance.” Realistically though, it looks like with the current state-of-the-art we’re limited to fairly low volume markets with limited numbers of participants.

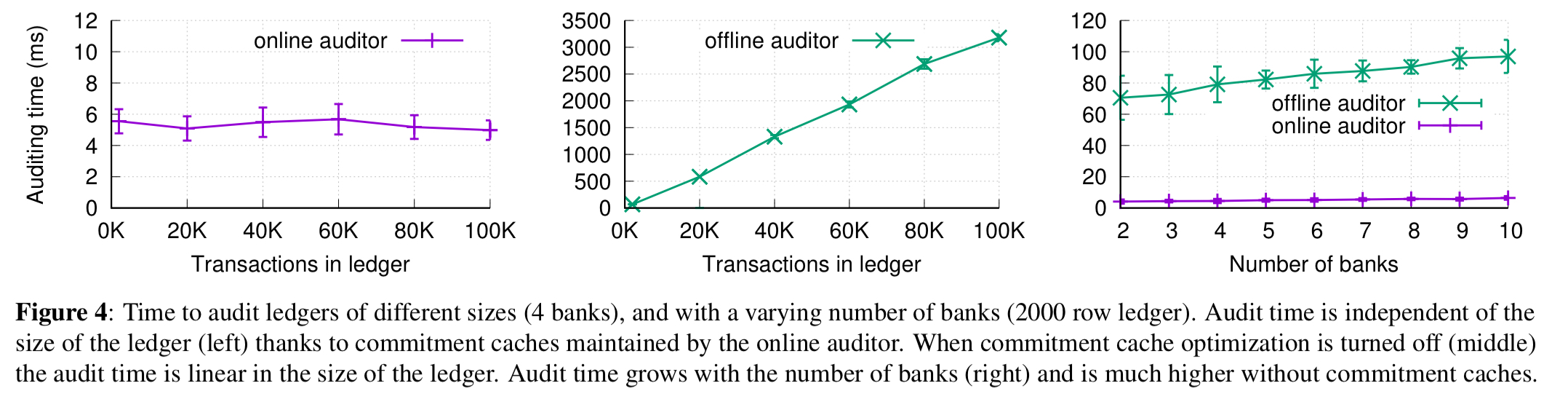
Using the commitment cache (online auditor below), auditing time is roughly constant. Without it (offline auditor) audit time is linear in the number of transactions in the ledger.