A static verification framework for message passing in Go using behavioural types Lange et al., ICSE 18

With thanks to Alexis Richardson who first forwarded this paper to me.

We’re jumping ahead to ICSE 18 now, and a paper that has been accepted for publication there later this year. It fits with the theme we’ve been exploring this week though, so I thought I’d cover it now. We’ve seen verification techniques applied in the context of Rust and JavaScript, looked at the integration of linear types in Haskell, and today it is the turn of Go!

Despite its popularity, the Go programming ecosystem offers little to no support for guaranteeing the correctness of message-passing concurrent programs. This work proposes a practical verification framework for message passing concurrency in Go…

Go’s channel-based concurrency model is inspired by process calculi. There is a rich body of work on process calculi-based verification for reasoning about safety and liveness properties of interactive systems. However, Go itself only enforces that messages exchange via communication channels adhere to the declared payload types, and at runtime offers just a “toy global deadlock detector.” Can we apply more of the process calculi based reasoning in the context of Go? It turns out that yes, we can.

The Godel Checker enables verification that Go programs are free of global deadlocks, as well as several Go specific safety properties (including channel safety). There is also support for detecting potentially problematic loops and partial deadlocks. At the core of the system is a translation from Go source code to a behavioural type model of the program. A model checker mCRL2 and termination checker (based on KiTTeL) can then be applied to the extracted behavioural types.

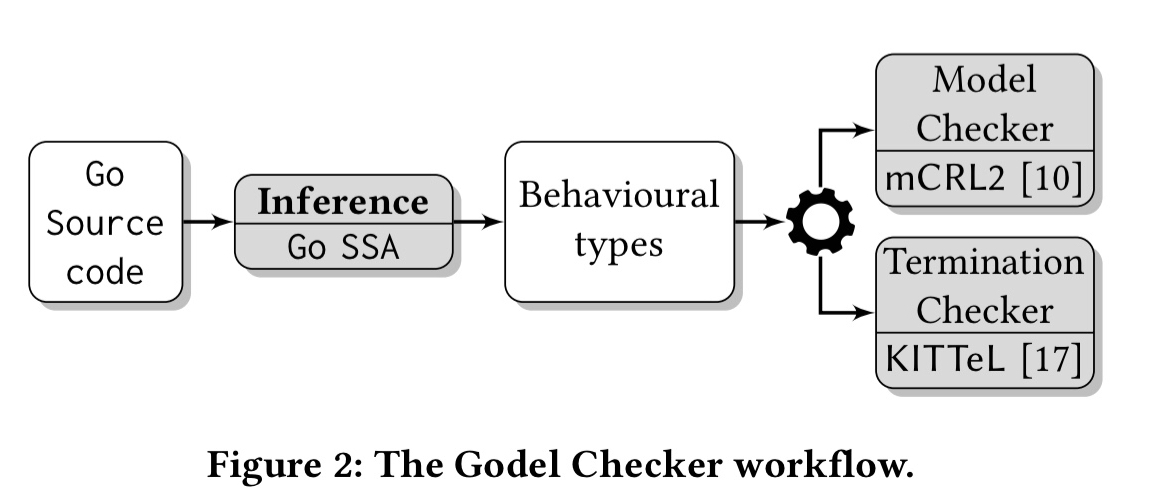
Verification of key safety and liveness properties for a variety of programs shows that Godel Checker can complete its analysis in just a few seconds for smaller programs, and just over a minute for the larger code bases tackled (up to 16 kloc). As a user, what’s nice about all this is that you don’t have to get involved with any of the formal machinery yourself, just supply the source code!

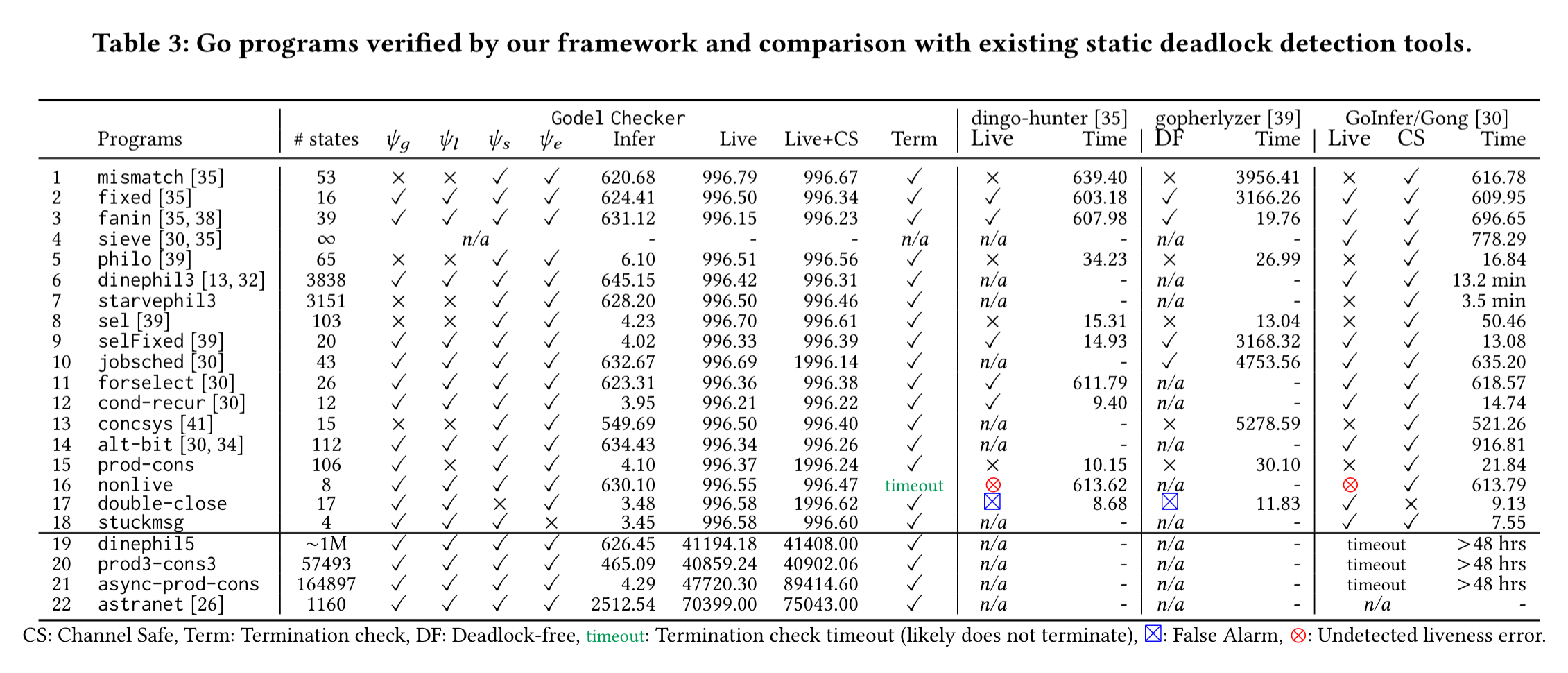
(Enlarge)

Common concurrency errors in Go programs

Godel Checker address three sources of common concurrency errors in Go programs: channel safety errors, global deadlocks, and partial deadlocks.

After a channel is closed, receive actions always succeed but any send or close actions raise a runtime error. Hence, “channels should be closed at most once and no message should be sent on closed channels.”

Go does have a built-in global deadlock detector that will signal at runtime if all goroutines in a program are stuck. We’d like to find out about the possibility (or hopefully, the absence of the possibility) of global deadlocks ahead of time. Moreover, when certain common libraries are imported, the global deadlock detector is silently disabled and hence global deadlocks are just ignored.

Then there’s the case when a program communication cannot progress even though only some of its goroutines are stuck. “This is known as a partial deadlock or as a failure of liveness.” Consider the following program:

Because ch1 is passed as both arguments to Consumer on line 16 the resulting system is not live: the second producer is not interacting with the consumer and its outputs will never be matched with their respective inputs.

From Go to Behavioural types

Behavioural types are a typing discipline in which types express the possible actions of a program in a fine-grained way. When applied to communication and concurrency, behavioural types act as an abstract specification of all communication actions that may be performed in a program. Moreover, behavioural types are an executable specification. They have a natural operational meaning and evolve throughout program execution.

For the program we saw above, the behavioural type looks like this:

Imperative control structures are transformed into recursive definitions, and data elements are erased.

In terms of types, global deadlock freedom (GDF) requires that if a communication action is available to fire, the type can always make progress. Thus a type as a whole is never globally stuck. Liveness, or partial deadlock freedom, is a stronger condition (every live type is also global deadlock free). Liveness states that all communications that can become enabled in a type can always eventually fire. (Replacing the call to cons(ch1,ch1) with cons(ch1,ch2) makes the type main() satisfy liveness).

In order to infer behavioural types from Go source code, the source is first converted to a static single assignment (SSA) intermediate representation (IR). The SSA IR conversion takes a Go program such as this:

And produces:

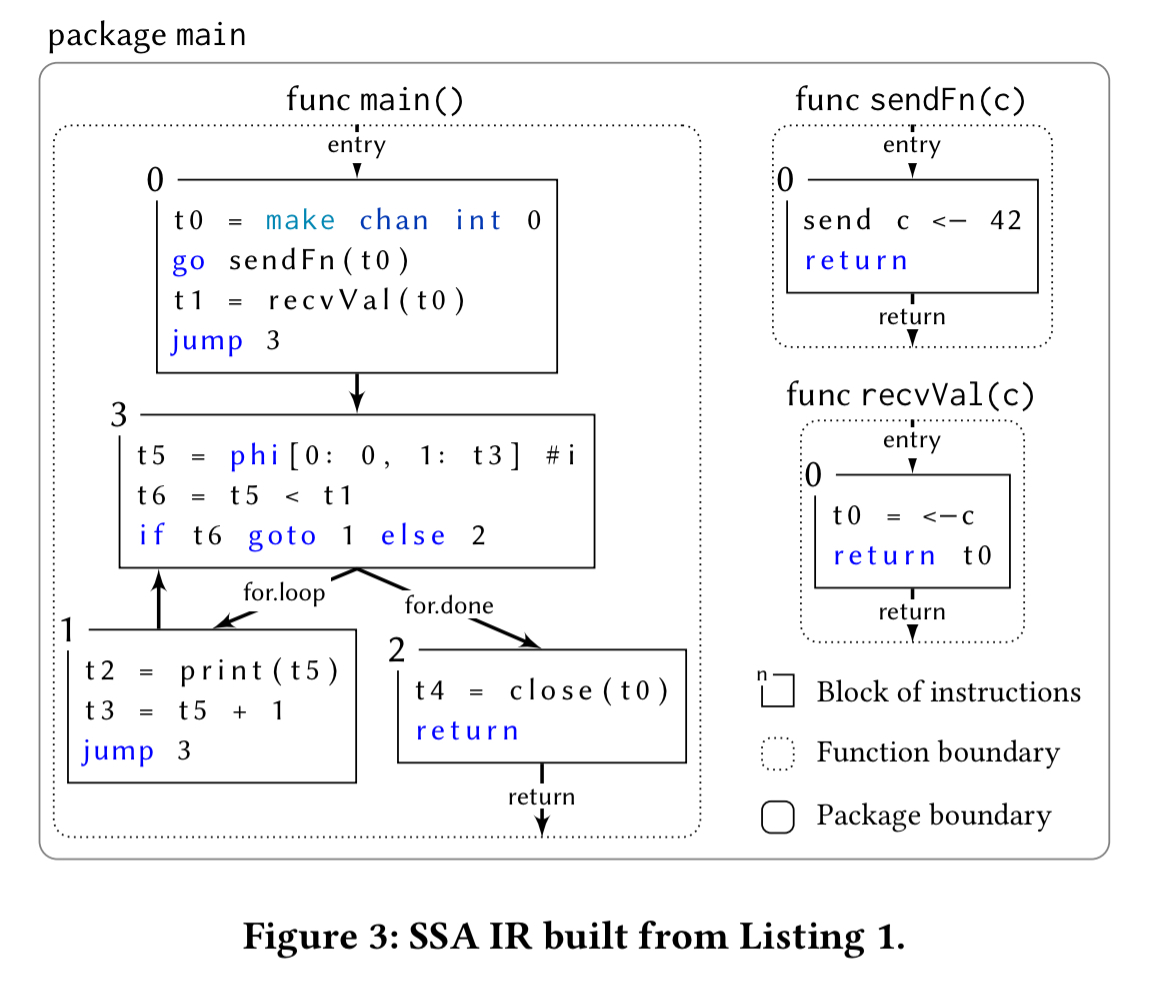
The main SSA instructions used in the IR are shown in the following table:

Given the SSA form, the next step is to soundly approximate the communication behaviour. A type signature is generated for every SSA block. The details of the algorithm are in section 3.2 of the paper. For our purposes we mostly just need to know that it is possible. At the end of this process, for Listing 1 above its SSA representation, the inferred behavioural type looks like this:

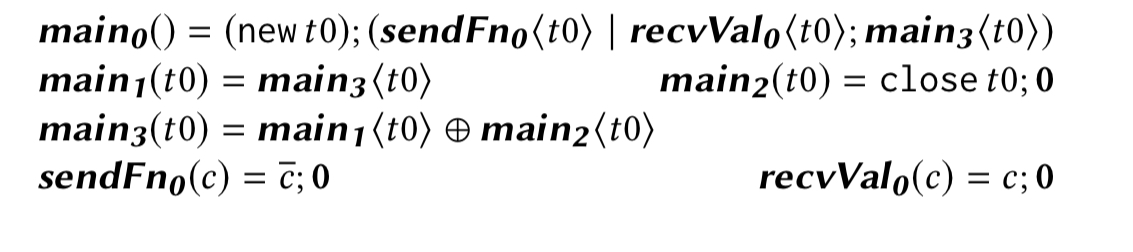
Model checking

We have our behavioural type model, and now we can proceed to verify its properties:

We proceed in three steps: (1) we generate a (finite) labelled transition system (LTS) for the types from a set of operational semantics rules; (2) we define properties of the states of the LTS in terms of the immediate actions behavioural types can take; and (3) we give safety and liveness properties expressed in the modal μ-calculus.

Finiteness is defined by the restriction that types cannot feature parallel composition or channel creation under recursion. Semantics for the types follow definitions from CCS (concurrent communication systems) and CSP (communicating sequential processes). A labelled transition system is built for the entry point type (it basically tells you how to move between states in the system). Given this representation, we can encode (and hence check) a number of useful liveness and safety properties in the μ-calculus. They look like this:

You’ll find a very concise guide to decoding those symbols in section 4 of the paper! Defined this way, the properties can be verified using the mCRL2 model checker.

When extracting behavioural types, conditionals are abstracted as a non-deterministic choice between the alternate behaviours in the then and else branches. This means that any data dependencies in the conditionals (e.g., testing the value of a variable) are not captured.

This coarse abstraction introduces a subtle interaction between non-terminating program behaviour and data-dependent communication wrt. liveness.

To address this, an additional termination analysis of loops is done using the KITTeL termination analyser. KITTeL actually targets C programs, but the syntax of Go is close enough to make it work with a translation to C functions. The analysis checks that the loop parameters are sufficient to make each loop eventually terminate. “_This enables us to pinpoint program locations where the liveness of types may not entail the analogue property in the program – if the termination analysis identifies the program as terminating, the liveness properties on types and programs coincide.”