Linear Haskell: Practical linearity in a higher-order polymorphic language Bernardy et al., POPL 18
I went in expecting this paper to be hard work. I mean, (a) it’s a POPL paper, (b) it’s about Haskell, and (c) not only is it about Haskell, it’s about an extension to the Haskell type system! I was more than pleasantly surprised — it’s highly readable, and it really opened my eyes to the benefits of linear types as integrated into an existing language.
Despite their obvious promise, and a huge research literature, linear type systems have not made it into mainstream programming languages, even though linearity has inspired uniqueness typing in Clean, and ownership typing in Rust. We take up this challenge by extending Haskell with linear types.
The extension is done in a non-invasive manner such that existing programs continue to typecheck, and existing datatypes can be used as-is, even in linear parts of the program.
A few quick definitions
Before we dive in, it’s worth a quick recap on some of the different words bandied around with respect to types and type systems that you’ll encounter in the paper.
- A linear function consumes its argument exactly once. A linear type system gives a static guarantee that a claimed linear function really is linear.
- An affine function consumes its argument at most once. An affine type system gives a static guarantee that a claimed affine function really is affine.
- A dependent type is a type whose definition depends on a value. For example, a dependent function’s return type may depend on the value of an argument, not just its type.
- Uniqueness (or ownership) types ensure that an argument of a function is not used elsewhere in an expression’s context even if the callee can work with the argument as it pleases. Linear types and uniqueness types have a ‘weak duality:’ ‘Seen as a system of constraints, uniqueness typing is a non-aliasing analysis, while linear typing provides a cardinality analysis.’
Why even bother? What’s so great about linear types?
The paper is focused around two main use cases for linear types. The one that really catches my imagination is encoding the usage protocol of a resource (e.g., you can’t read from a file before it is opened) in types. “Here, linearity does not affect efficiency, but rather eliminates many bugs.” We’ll return to some examples of this later in this post. It seems like there’s a very nice and natural fit to protocols in distributed systems (a bit like we looked at with Disel yesterday).
The second use case is safe update in place, and the reason we’re interested in that is efficiency – if we know it’s safe to update a value in place we don’t need to worry about making copies, or mutual exclusion mechanisms.
The linear arrow
We need a way to distinguish between linear (consume exactly once) objects, and unrestricted objects. One approach is to have two different kinds of types: a linear kind and a regular/unrestricted kind. The alternative is to have linear arrows, which more closely follows linear logic. For integration with Haskell, “after scratching the surface we have discovered that ‘linearity via arrows’ has an edge over ‘linearity via kinds.’”
The linear arrow guarantees that if
is consumed exactly once, then the argument
is consumed exactly once. The linear arrow specifies how a function uses its argument, and does not restrict the arguments to which the function can be applied.
The definition of consumed exactly once depends on the type of the value concerned:
- To consume a value of atomic base type (like Int or Ptr) exactly once, just evaluate it
- To consume a function value exactly once, apply it to one argument, and consume its result exactly once
- To consume a pair exactly once, pattern-match on it, and consume each component exactly once
- In general, to consume a value of an algebraic datatype exactly once, pattern-match on it and consume all its linear components exactly once.
Encoding protocols
Consider the API for files, shown below:

Nothing here stops us reading a file after we have closed it, or forgetting to close it. If we specify the interface using linear types we can do better:

The IO monad has been generalised to express whether or not the returned value is linear. A multiplicity type parameter is added, which can be 1 (linear) or (unrestricted), indicating a linear or unrestricted result respectively. Note that
openFile returns indicating that the returned file must be used linearly.
readLine consumes the File and produces a new one. The ByteString returned by readLine is unrestricted.
A function to read the first line can now be written like this:

There’s a lot to take in all at once here, and it wasn’t until much later in the paper (section 5.2) that it ‘clicked’ for me. There we find another protocol example. Consider the BSD socket API, and its usage for TCP (create a socket, bind it to an address, listen for incoming traffic, accept connection requests, and receive traffic). There’s a protocol for using the API that needs to be followed.
In the File API [above] we made files safer to use at the cost of having to thread a file handle explicitly: each function consumes a file handle and returns a fresh one. We can make this cost into an opportunity: we have the option of returning a handle with a different type from that of the handle we consumed! So by adjoining a phantom type to sockets to track their state, we can effectively encode the proper sequencing of socket actions.
As an example, here’s a wrapper specialised for TCP:

That’s pretty cool! If the program statically type checks, then you know you’re following the protocol correctly. This is taking us into the world of behavioural types, of which more tomorrow!
Instead of implementing a whole new set of wrapper functions for every protocol as above, the wrappers in the evaluation implementation are actually implemented with “a generic type-state evolving according the rules of a deterministic automaton. Each protocol can define its own automaton, which is represented as a set of instances of a type class.”
Update-in-place and efficiency
The Haskell language provides immutable arrays, built with the function array. But if we look under the hood, we’ll find an ‘unsafeFreeze’ :

Why is unsafeFreeze unsafe? The result of (unsafeFreeze ma) is a new immutable array, but to avoid an unnecessary copy, it is actually ma. The intention is, of course, that that unsafeFreeze should be the last use of the mutable array; but nothing stops us continuing to mutate it further, with quite undefined semantics. The “unsafe” in the function name is a GHC convention meaning “the programmer has a proof obligation here that the compiler cannot check.”
Using linear types we can define a more secure and less sequential interface (see §2.2), opening the possibility of exploiting more parallelism at runtime. Jumping ahead once more to section 5.1, we find an example that illustrates the power of the approach. Typically distributed services communicate via serialised data in text or binary formats, with the data being deserialised, processed, and then the result serialised for transmission.
The process is inefficient, but nevertheless tolerated, because the alternative — computing directly with serialised data — is far too difficult to program… Here is an unusual case where advanced types can yield performance by making it practical to code in a previously infeasible style: accessing serialised data at a fine grain without copying it.
Here’s an example of type-safe read-only access to serialised data for a particular datatype: a type-safe serialisation layer is one which reads byte ranges only at the type and size they were originally written.

A Packed value is a pointer to raw bits (a bytestring), indexed by the types of the values contained within… It is precisely to access multiple, consecutive fields that Packed is indexed by a list of types as its phantom type parameter. Individual atomic values (Int, Double, etc.) can be read one at at time with a lower-level read primitive…
A serialised data constructor needs to write a tag, followed by the fields. A linear write pointer ensures all fields are initialised in order. The type Needs is used for write pointers, parameterised by a list of things remaining to be written, and the type of the final value which will be initialised once those writes are performed. That leads to elegant operation specs such as:
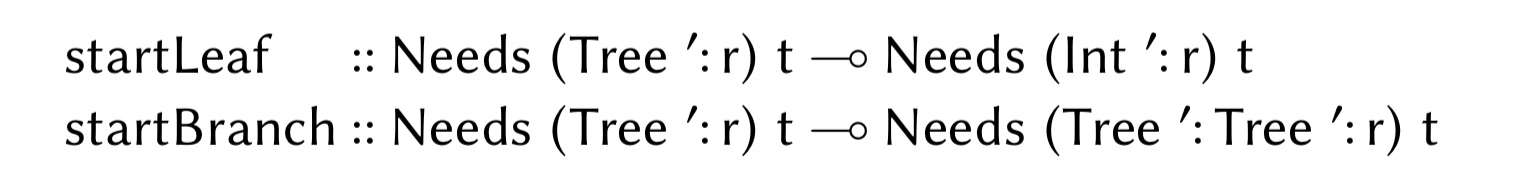
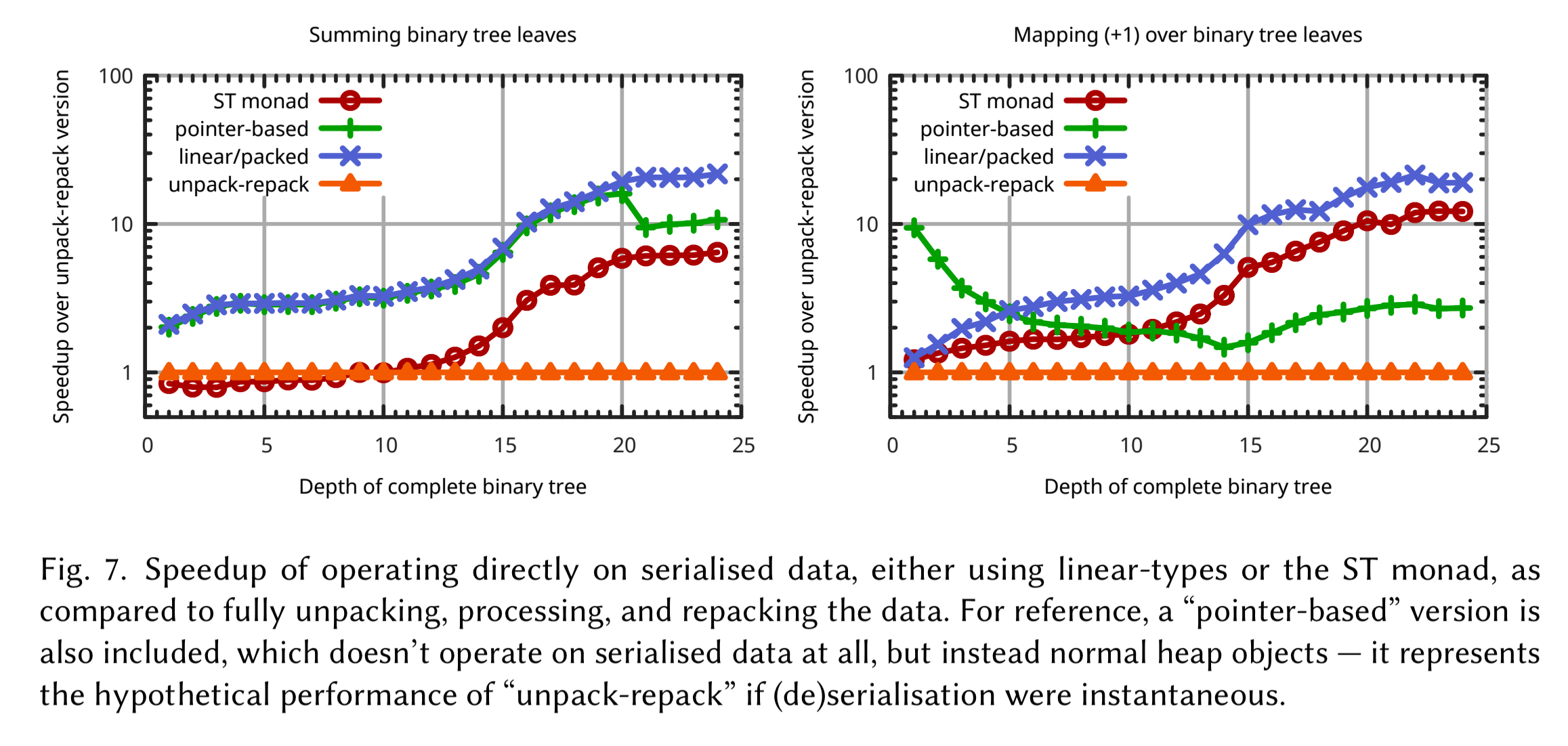
Compared to this baseline (the traditional approach), processing the data directly in its serialised form results in speedups of over 20x on large trees. What linear types makes safe, is also efficient.
Calculus
Once again, I’ve had to leave out lots of (important!) information to condense the gist of the paper into 1500 words or so. Critically, §3 defines a core calculus for linear Haskell (with a neat solution for combining linear and free multiplicities). The operational semantics are given in an extended version of the paper.
It is hard to reason on a lazy language with mutation. But what we show is that we are using mutation carefully enough so that they behave as pure data…
Implementation
Linear Haskell affects 1,152 lines of GHC (out of more than 100K lines of code). The initial evaluation was to compile a large existing code base together with the following two changes:
- All (non-GADT) data constructors are linear by default, as implied by the new type system
- The standard list functions are updated to have linear types
Under these conditions 195K lines of Haskell compiled successfully, providing preliminary evidence of backwards compatibility.