Differential Dataflow – McSherry et al. 2013
The ability to perform complex analyses on [datasets that are constantly being updated] is very valuable; for example, each tweet published on the Twitter social network may supply new information about the community structure of the service’s users, which could be immediately exploited for real-time recommendation services or the targeting of display advertisements.
Effective incremental processing of such a stream of updates, where the processing involves iterative computation and looping constructs is a tough problem. “For example, no previously published system can maintain in real time the strongly connected component structure in the graph induced by Twitter mentions.”
This paper, which is a companion to the Naiad paper that we looked at last week, introduces a model for incremental iterative computation which the authors call differential computation. Differential computation deals with how to update a computation when its inputs change. Combining this with dataflow techniques to track dependencies and update global state when local updates occur yields differential dataflow – or as I like to think of it, ‘deltaflow’.
Here’s the headline grabber:
We have implemented differential dataflow in a system called Naiad, and applied it to complex graph processing queries on several real-world datasets. To highlight Naiad’s characteristics, we use it to compute the strongly connected component structure of a 24-hour window of Twitter’s messaging graph (an algorithm requiring doubly nested loops, not previously known in a data-parallel setting), and maintain this structure with sub-second latency, in the face of Twitter’s full volume of continually arriving tweets.
Differential Computation
Borrowing terminology from data-parallel dataflow systems, consider that computation is performed by functions called operators, whose inputs and outputs are collections. Over the course of a computation, there may be multiple versions of a collection (for example, a new version is created when a collection is passed through an operator that mutates it, or an input collection can change with new external updates). The versions of a particular collection over time form a collection trace, which imposes a partial ordering on versions. For example, the ordering may be based on epoch numbers. A computation’s inputs and outputs for streaming computations are therefore collection traces.
Given a collection trace, we can form a difference trace. For a collection A, the difference δAt at time t is simply the difference between the collection at time t, At, and the collection at time t-1, At-1. δA0 is defined to be A0. Thus a difference trace comprises the initial state of the collection followed by a sequence of deltas. Recreating the state of the collection at time t is simply a matter of summing all the deltas from 0 to t.
A straightforward incremental operator that takes collections of type A as input and produces collections of type B as output would normally compute the following:
δBt = Op(At-1 + δAt) – Op(At-1)
Thus it needs to keep as state only the most recent versions of the collections: At = At-1 + δAt and Bt = Bt-1 + δBt.
Iteration, in particular loops that end up reintroducing the output of an operation back into its input, mess up this neat scheme.
Unfortunately, the sequential nature of incremental computation implies that differences can be used either to update the computation’s input collections or to perform iteration, but not both. To achieve both simultaneously, we must generalize the notion of a difference to allow multiple predecessor versions, as we discuss in the next subsection.
Differential computation is a generalization of the incremental computation outlined above.
The data are still modeled as collections At, but rather than requiring that they form a sequence, they may be partially ordered. Once computed, each individual difference is retained, as opposed to being incorporated into the current collection as is standard for incremental systems. This feature allows us to carefully combine differences according to reasons the collections may have changed, resulting in substantially smaller numbers of differences and less computation.
With a partial ordering, there may not be a unique predecessor, so how can we give meaning to δAt? The answer is to define it as the difference between At, and the sum of all δAs where s < t according to the partial ordering.
Now we need to keep the deltas, but as a result we can compute:
As an example of a useful real-world partial ordering consider an iterative computation over a collection with a stream of updates to that same collection. If Ai,j represents the state of the collection A after the ith iteration on the jth input version, then neither A0,1 nor A1,0 is ‘less than’ the other. And in accordance with the differential computation formula above, neither will be used in the computation of the other.
This independence would not be possible if we had to impose a total order on the versions, since one of the two would have to come first, and the second would be forced to subtract out any differences associated with the first.
Consider the derivation of the difference δA1,1 = A1,1 – (δA0,0 + δA0,1 + δA1,0) . By keeping the deltas we can efficiently compute this, but with any imposed total order we would have to do rework.
Section 3.4 in the paper provides the pseudocode for implementing an operator that can compute on differences. An important but subtle point is that an input delta can continue to affect output deltas into the future, even at points in time when the operators inputs themselves are not changing. Thus in order to efficiently compute output deltas the full input difference traces must be stored and indexed in memory.
In the Naiad prototype implementation this trace is stored in a triply nested sparse array of counts, indexed first by key k, then by lattice version t, then by record r. Naiad maintains only non-zero counts, and as records are added to or subtracted from the difference trace Naiad dynamically adjusts the allocated memory. With δA and δB indexed by version, At and Bt can be reconstructed for any t, and δz computed explicitly, using the pseudocode of Algorithm 1. While reconstruction may seem expensive, and counter to incremental computation, it is necessary to be able to support fully general operators for which the programmer may specify an arbitrary (non-incremental) function to process all records. We will soon see that many specific operators have more efficient implementations…
It is possible to consolidate difference traces into the equivalent of a checkpoint at time t, once it is known that no further updates prior to t will be forthcoming.
Differential Dataflow
A C# program using LINQ extensions is transformed into a cyclic dataflow graph for execution. The LINQ extensions include a FixedPoint method for loop execution and a PrioritizedFixedPoint method which can also control the order in which records are introduced into the loop body. Following the pattern described in the Naiad paper, both are implemented with an ingress vertex, an egress vertex, and a feedback vertex that provides the output of the loop body as input to subsequent operations.
On this general foundation, Naiad provides specialized operators for data-parallel processing (e.g. in Join and GroupBy); pipelined processing (e.g. for Select, Where, Concat, …); more efficient Join processing; and aggregation.
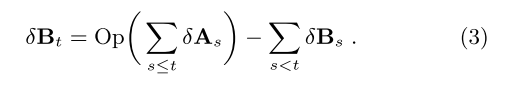
3 thoughts on “Differential Dataflow”
Comments are closed.