Establishing software root of trust unconditionally Gligor & Woo, NDSS’19
The authors won a best paper award for this work at NDSS this year. The main result is quite something, but as you might expect the lines of argument are detailed and not always easy to follow (and certainly not critically!) for non-experts like me. I’ll use today’s write-up to convey the big ideas as I understand them. Close reading of the original paper (and it’s accompanying technical report) will be essential if you then want to dig deeper.
The problem: establishing a root of trust
Root of trust (RoT) establishment on an untrusted system ensures that a system state comprises all and only content chosen by the user, and the user’s code begins execution in that state. All implies that no content is missing, and only that no extra content exists. If a system state is initialized to content that satisfies security invariants and RoT establishment succeeds, a user’s code begins execution in a secure initial state.
That is to say, even in the presence of persistent malware e.g. in the firmware of peripheral controllers, network interface cards, disk and USB controllers, and so on, root of trust can assure us that the system has booted into a known and trusted state (or alternatively, uncover the presence of malware with high probability).
The word “unconditionally” from the paper title is also highly significant here. In this context it means there are no external dependencies on e.g. secrets, trusted hardware modules, or special instructions (e.g. TPMs, SGX, …), and no polynomial bounds on an adversaries computing power (so for example they still work even in a post-quantum world).
By definition, a solution to a security or cryptography problem is unconditional if it depends only on the existence of physical randomness and the ability to harvest it… We know of no other protocols that establish RoT provably and unconditionally. Nor do we know any other software security problem that has been solved unconditionally in any realistic computational model.
The main result: unconditional RoT establishment
The untrusted system (system to be verified) is connected to a trusted local verifier. The adversary can do pretty much anything: firmware attacks, remote control of malware and secret extraction over a network channel, reading from and writing to the verifier’s I/O channel, and unlimited computing power on tap. The adversary does not however have access to the verifier’s device and external source of true random number.
The big picture comes together like this:
- The verifier asks the system to initialise its random access memory M and register set R to the chosen content (i.e., known good state of a trustworthy program).
- Then the verifier selects a random nonce and sends it to the system with a challenge to perform a (very!) carefully chosen computation over M and R and the nonce.
- The computation is such that it is space-time optimal (i.e., not possible to do it any faster than time t, and not possible to use any less space than m).
- The computation is non-interruptible, and is timed with very high accuracy. The verifier expects a result after time t, such that there isn’t time to slip in even a single additional instruction.
- Moreover, the computation is second pre-image free. This means that you can’t easily find a second input (e.g., a somehow corrupted version of the desired system state in this case) that produces the same output as the original input (the system state we expect the system to be in).
Intuitively, second pre-image freedom and m-t optimality can jointly prevent an adversary from using fewer than m words or less time than t, or both, and hence from leaving unaccounted for content (e.g. malware) or executing arbitrary code in the system.
So all we need now is a super-accurate timer, and a rather special computation family…
Building blocks
The lower bounds of a computation are established by a proof that holds for all possible algorithms for performing it. For example, if we’re going to add two numbers we at least need to look at those two numbers… A particular algorithm for that computation is space-time optimal if its bounds match the space and time lower bounds of its computation. Asymptotic lower bounds are no use here (because an adversary might always be able to find slightly better concrete bounds), and nor are purely theoretical lower bounds: we must have a concrete algorithm that exactly matches them. Moreover, the algorithm needs to be executable in a realistic computer model (e.g. , accounting for general ISAs, I/Os, interrupts, multi-processors, and so on).
Word Random Access Machine (WRAM) models are the closest to real computers. The cWRAM model has a constant word length and at most two operands per instruction.
The cWRAM includes all known register-to-register, register-to-memory, and branching instructions of real system ISAs, as well as all integer, logic, and shift/rotate computation instructions… All cWRAM instructions execute in unit time.
Polynomial evaluation based on Horner’s rule can be implemented in cWRAM using a sequence of four instructions per step. A d-degree polynomial can be evaluated in d steps in a Horner-rule program. I.e., it can form the basis of our special computation.
The honest one-time evaluation of
by a Horner-rule program is uniquely space-time optimal whenever the cWRAM execution time and memory are simultaneously minimized; i.e., no other programs can use fewer than both
storage words and
time units.
(Proof in appendix B of the accompanying technical report).
What kind of polynomials can we evaluate that will have the desired second pre-image resistance? Good old hash functions! (As an aside, it’s quite amazing how many incredible uses hash functions have been put to!). We’ll compute the equivalent of k-independent and (almost) universal hash functions over the contents of the memory, the registers, and the nonce. The family H of randomized polynomials defined in section IV.A of the paper have the desired property.

Theorem 3 asserts that no program can use both fewer than storage words and
time units in an honest one-time evaluation of Horner(H). And theorem 5 asserts that no adversary can do better with probability at most
(p is the big prime we used to establish the family H).
Putting it all together
A system comprises c connected devices, where device i has random access memory and processor registers
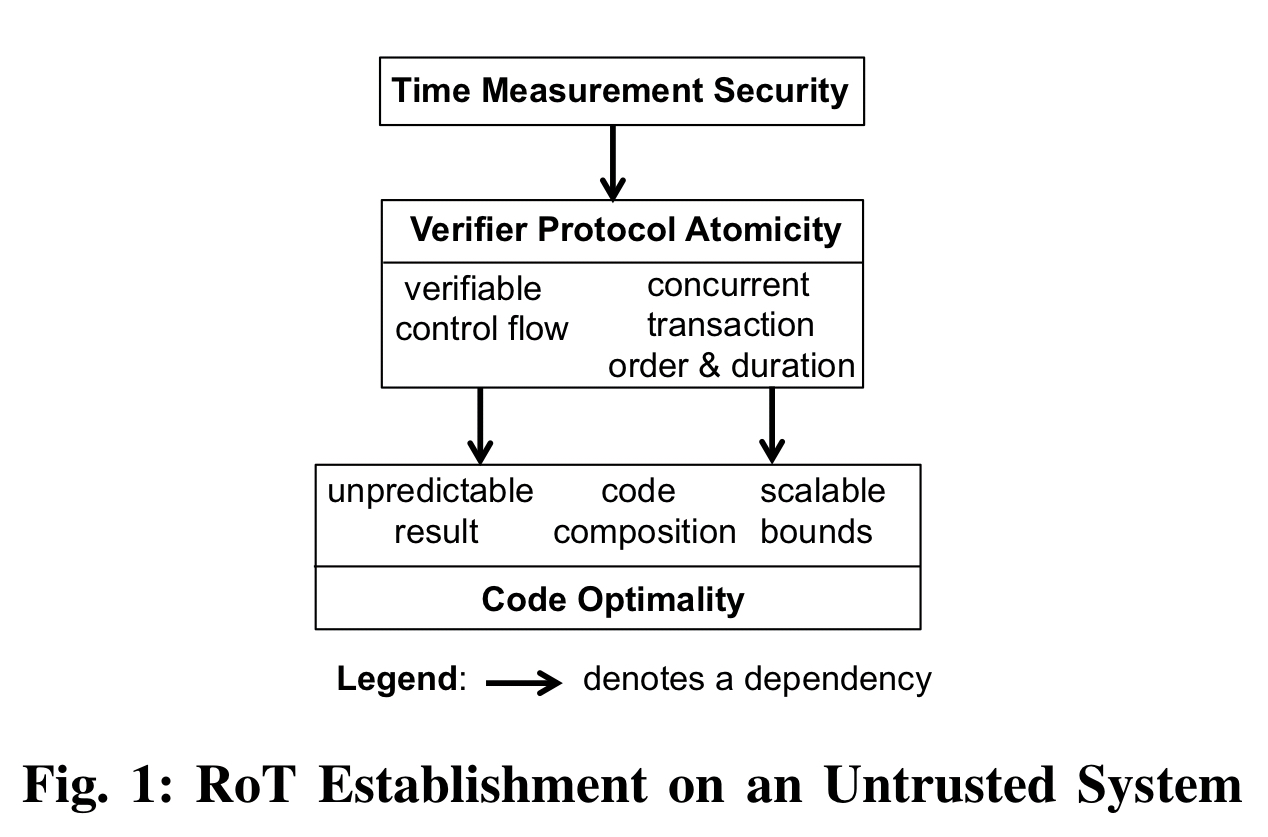
. We have to verify all of the devices concurrently, with a transactional verifier protocol such that verification only passes if all checks pass. The difference between the start and end times of any two verification programs must be small enough that neither device can detectably perform any computation for the other. The values of d and k in the Horner(H) problem for a device can be chosen such that the duration requirement is satisfied across devices of varying speed.
To enable accurate time measurement we need to:
- Attach the verifier device via a DMA interface such that there is no peripheral device controller in the path, and the channel delay and variation is small enough that any untrusted communication can be detected. The verifier could also run as a co-processor connected to the main system bus.
- Disabling caches, virtual memory, and the TLB (this can be done verifiably as shown in theorem 6 in section IV.E)
- Eliminating the effects of random clock jitter using random sequential protocols as developed for embedded real-time systems.
Implementation
Performance measurements for Horner-rule evaluation of randomised polynomials show implementation practicality on a commodity hardware platform.
The timing for k=64 and d=10M is 54,578ms. For the baseline d = 128M [covering the entire SDRAM], the running time is close to 700 seconds…
Good things come to those who wait!
The last word
In this paper we showed that, with a proper theory foundation, RoT establishment can be both provable and unconditional. We know of no other software security problem that has had such a solution, to date. Finally, the security of time measurements on untrusted systems has been a long-standing unsolved engineering problem. Here, we also showed that this problem can be readily solved given the provable atomicity of the verifier’s protocol.