Obfuscated gradients give a false sense of security: circumventing defenses to adversarial examples Athalye et al., ICML’18
There has been a lot of back and forth in the research community on adversarial attacks and defences in machine learning. Today’s paper examines a number of recently proposed defences and shows that most of them rely on forms of gradient masking. The authors develop attack techniques to overcome such defences, and 9 analyse defences from ICLR 2018 claiming to protect against white-box attacks. 7 of these turn out to rely on obfuscated gradients, and 6 of these fall to the new attacks (and the other one partially succumbs). Athalye et al. won a best paper award at ICML’18 for this work.
One of the great things about work on adversarial attacks and defences, as we’ve looked at before, is that they illuminate the strengths and weaknesses of current technology. Depending on the threat model you choose, for my own part I’m currently of the opinion that we’re unlikely to find a robust adversarial defence without a more radical re-think of how we’re doing image classification. If we’re talking about the task of ‘find an image that doesn’t fool a human, but does fool a neural network’ then I think there will always be gaps to exploit until we incorporate more human-like (e.g., higher level semantic understanding) reasoning into our classifiers. Not that the human system itself can’t be fooled of course (e.g., optical illusions).
Breaking gradient descent
A defense is said to cause gradient masking if it “does not have useful gradients” for generating adversarial examples; gradient masking is known to be an incomplete defense to adversarial examples. Despite this, we observe that 7 of the ICLR 2018 defenses rely on this effect.
Some defenses break gradient descent deliberately, others may do it unintentionally. Here are five clues that something isn’t right:
- One-step attacks perform better than iterative attacks. Iterative attacks are strictly stronger, so this shouldn’t be the case. If single-step methods are working better, it’s a sign the iterative attack is becoming stuck at a local minimum.
- Black-box attacks work better than white-box attacks. The black-box threat model is a strict subset of white-box attacks, so white-box attacks should perform better. When a defense obfuscates gradients, then black-box attacks (which don’t use it) often perform better. (Since practical black-box attacks are possible and we can also find e.g. universal adversarial perturbations the utility of a defense that excludes such attack modes seems rather limited anyway to me).
- Unbounded attacks do not reach 100% success. With unbounded distortion, any classifier should eventually fail. An attack that doesn’t achieve this should be improved (i.e., it’s a weak attack, not necessarily a strong defense).
- Random sampling finds adversarial examples (where a gradient-based attack does not).
- Increasing the distortion bound does not increase success. We expect a monotonically increasing attack success rate with increasing distortion bound.
Three ways that a defense might break gradient descent are shattering, stochastic gradients, and exploding & vanishing gradients:
- Shattered gradients are caused when a defense is “non-differentiable, introduces number instability, or otherwise causes a gradient to be nonexistent or incorrect.”
- Stochastic gradients are a result of randomization – either introduced in the network itself, or in the inputs being fed to the network
- Exploding and vanishing gradients are often caused by defenses that consist of multiple iterations of neural network evaluation, feeding the output of one computation into the next.
Overcoming masked gradients
Shattered gradients can be overcome using a technique the authors call ‘Backward Pass Differentiable Approximation’ (BPDA). Think of a secured neural network (i.e., one that has been hardened against adversarial attacks) as being a composition of some hardening function and a regular pre-trained classifier
such that the hardened classifier
. For example,
might be a denoising function designed to remove perturbations introduced by an adversary. If
itself is smooth and differentiable we can often compute gradients through the combined network
. Even if it isn’t differentiable, we know that by construction in a local area it is close to the identify function (i.e.
). So we conduct an attack by performing forward propagation through the neural network as usual, but replacing
with the identity function (or even simpler, just the evaluation of
) during backpropagation. The full (general) version of BPDA operates by finding and replacing any non-differentiable layer
with a differentiable approximation
such that
. As before, we use the vanilla network on the forward pass, and substitute
on the backward pass.
To attack a network that relies on stochastic gradients, it is necessary to estimate the gradient of the stochastic function. ‘Expectation over Transformation’ (EOT) can be used to compute the gradient over an expected transformation to an input. Given a transformation function EOT optimises the expectation over
. “The optimization problem can be solved through gradient descent… differentiating through the classifier and transformation, and approximating the expectation with samples at each gradient descent step.”
Vanishing or exploding gradients can be addressed through reparameterization. Suppose differentiating leads to a problem. We can introduce a new differentiable function
such that
and
for all
. We can now compute gradients through
and circumvent the defense. (§4.3).
How the ICLR 2018 defenses stack up
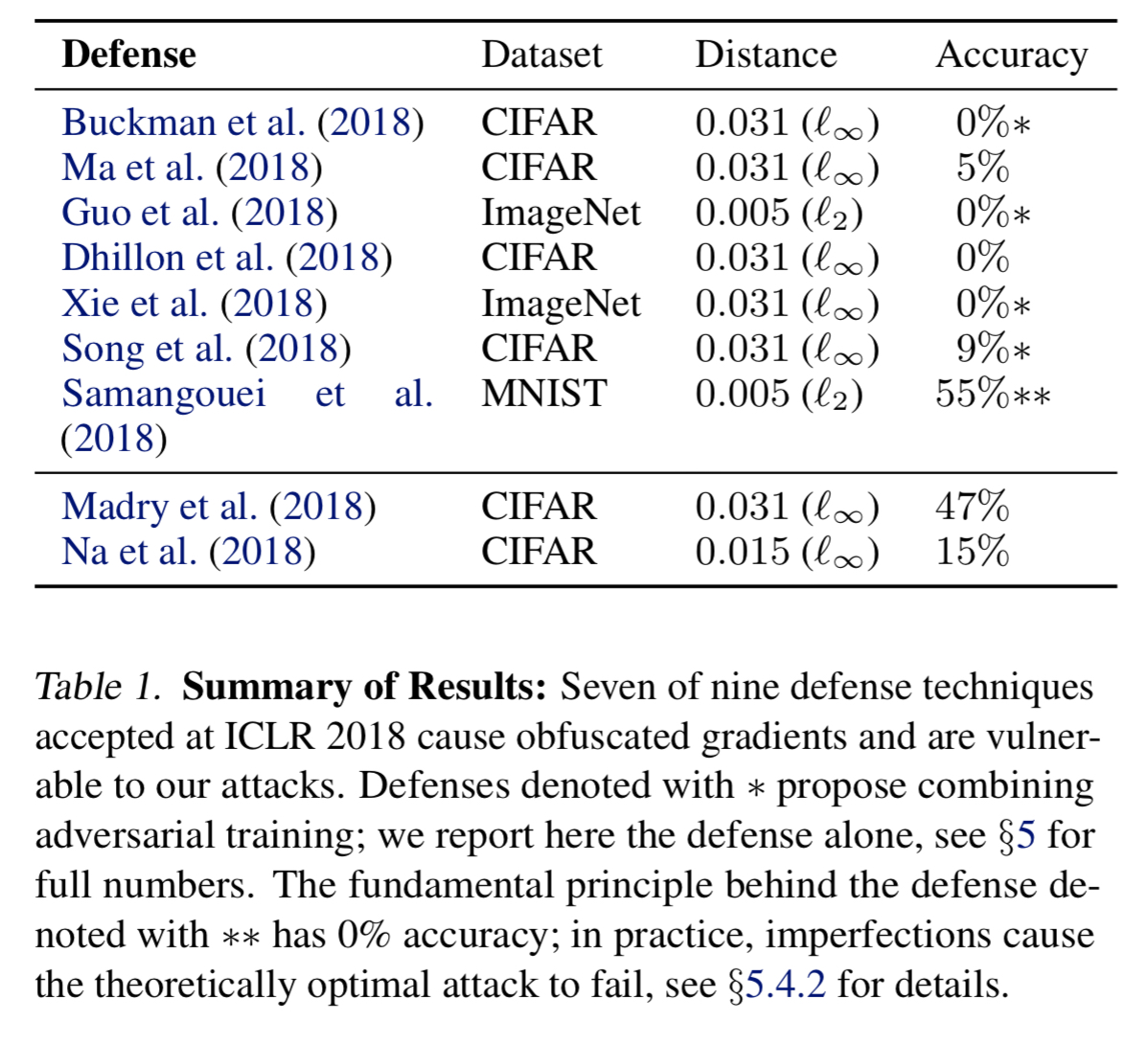
Section 5 of the paper works through nine defenses from ICRL 2018 that claim robustness in a white-box threat model. Seven of the nine turn out to rely on some form of obfuscated gradients. For these the authors use the techniques described above to successfully attack them.
Thermometer encoding is an example of a defense that relies on gradient shattering at its core. Image pixels are mapped to l-dimensional vectors such as ‘111110000’, where the number of leading 1’s indicates the temperature (colour value) of a pixel. A BPDA attack reduces model accuracy to 30% (worse than if thermometer encoding were not used at all!).
Examples of transformation based defenses include image cropping and rescaling, bit-depth reduction, JPEG compression, randomly dropping pixels and replacing them using total variance minimization, and image quilting (reconstructing images by replaces small patches with patches taken from ‘clean’ images).
It is possible to bypass each defense independently (and ensembles of defenses usually are not much stronger than the strongest sub-component)… with our attack, we achieve 100% targeted attack success rate and accuracy drops to 0% for the strongest defense under the smallest perturbation budget…
Image cropping and rescaling are circumvented using EOT. Bit depth reduction and JPEG compression are circumvented using BPDA and the identity function on the backward pass. Random pixel replacement and quilting are defeated using a combination of EOT and BPDA.
PixelDefend and Defense-GAN both use generators to project input images back onto a data manifold before feeding them into a classifier. Informally, this is intended to ‘purify’ them by avoiding low-probability regions in the data distribution.
PixelDefend can be defeated using BPDA, and DefenseGAN can also be evaded with BPDA, though only at a 45% success rate.
See section 5 in the paper for more details and discussion of the other defenses.
… we hope that future work will be able to avoid relying on obfuscated gradients (and other methods that only prevent gradient descent-based attacks) for perceived robustness, and use our evaluation approach to detect when this occurs.