Matrix capsules with EM routing Anonymous 😉, Submitted to ICLR’18
(Where we know anonymous to be some combination of Hinton et al.).
This is the second of two papers on Hinton’s capsule theory that has been causing recent excitement. We looked at ‘Dynamic routing between capsules’ yesterday, which provides some essential background so if you’ve not read it yet I suggest you start there.
Building on the work of Sabour et al., we have proposed a new capsule network architecture in which each capsule has a logistic unit to represent the presence of an entity and a 4×4 pose matrix to represent the relationship between that entity and the viewer. We also introduced a new iterative routing procedure between capsule layers, making use of the EM algorithm, which allows the output of each lower-level capsule to be routed to a capsule in the layer above so that each higher-level capsule receives a cluster of similar pose votes, if such a cluster exists.
This revised CapsNet architecture (let’s call it CapsNetEM) does very well on the smallNORB dataset, which contains gray-level stereo images of 5 classes of toy: airplanes, cars, trucks, humans, and animals. Every individual toy is pictured at 18 different azimuths, 9 elevations, and 6 lighting conditions.

By ‘very well’ I mean state-of-the-art performance on this dataset, achieving a 1.4% test error rate (the CapsNet architecture we looked at yesterday achieves 2.7%). The best prior reported result on smallNORB is 2.56%. A smaller CapsNetEM network with 9 times fewer parameters than the previous state-of-the-art also achieves 2.2% error rate.
A second very interesting property of CapsNetEM demonstrated in this paper is increased robustness to some forms of adversarial attack. For both general and targeted adversarial attacks using an incremental adjustment strategy (white box) such as that described in ‘Explaining and harnessing adversarial examples,’ CapsNetEM is significantly less vulnerable than a baseline CNN.
…the capsule model’s accuracy after the untargeted attack never drops below chance (20%) whereas the convolutional model’s accuracy is reduced to significantly below chance with an epsilon of as small as 0.2.
We’re not out of the woods yet though – with black box attacks created by generating adversarial examples with a CNN and then testing them on both CapsNetEM and a different CNN, CapsNetEM does not perform noticeably better. Given that black box attacks are the more likely in the wild, that’s a shame.
Capsules recap
The core capsules idea remains the same as we saw yesterday, with network layers divided into capsules (note by the way the similarity here with dividing layers into columns), and capsules being connected across layers.
Viewpoint changes have complicated effects on pixel intensities but simple, linear effects on the pose matrix that represents the relationship between an object or object-part and the viewer. The aim of capsules is to make good use of this underlying linearity, both for dealing with viewpoint variation and improving segmentation decisions.
Each capsule has a logistic unit to represent the presence of an entity, and a 4×4 pose matrix which can learn to represent the relationship between that entity and the viewer. A familiar object can be detected by looking for agreement between votes for its pose matrix. The votes come from capsules in the preceding network layer, based on parts they have detected.
A part produces a vote by multiplying its own pose matrix by a transformation matrix that represents the viewpoint invariant relationship between the part and the whole. As the viewpoint changes, the pose matrices of the parts and the whole will change in a coordinated way so that any agreement between votes from different parts will persist.
To find clusters of votes that agree, a routing-by-agreement iterative protocol is used. The major difference between CapsNet and CapsNetEM is the way that routing-by-agreement is implemented.
Limitations of routing-by-agreement using vector lengths
In CapsNet, the length of the pose vector is used to represent the probability that an entity is present. A non-linear squashing function keeps the length less than 1. A consequence though is that this “prevents there from being any sensible objective function that is minimized by the iterative routing procedure”.
CapsNet also uses the cosine of the angle between two pose vectors to measure their agreement. But the cosine (unlike the log variance of a Gaussian cluster) is not good at distinguishing between good agreement and very good agreement.
Finally, CapsNet uses a vector of length rather than a matrix with
elements to represent a pose, so its transformation matrices have
parameters rather than just
.
CapsNetEM overcomes all of these limitations with a new routing-by-agreement protocol.
Using Expectation Maximisation (EM) for routing-by-agreement
Let us suppose that we have already decided on the poses and activation probabilities of all the capsules in a layer and we now want to decide which capsules to activate in the layer above and how to assign each active lower-level capsule to one active higher-level capsule.
We start by looking at a simplified version of the problem in which the transformation matrices are just the identity matrix, essentially taking transformation out of the picture for the time being.
Think of each capsule in a higher layer as corresponding to a Gaussian, and the outputs of each lower level capsule as data points. Now the task essentially becomes figuring out the fit between the data points produced by the lower layer capsules, and the functions defined by the higher layer Gaussians.
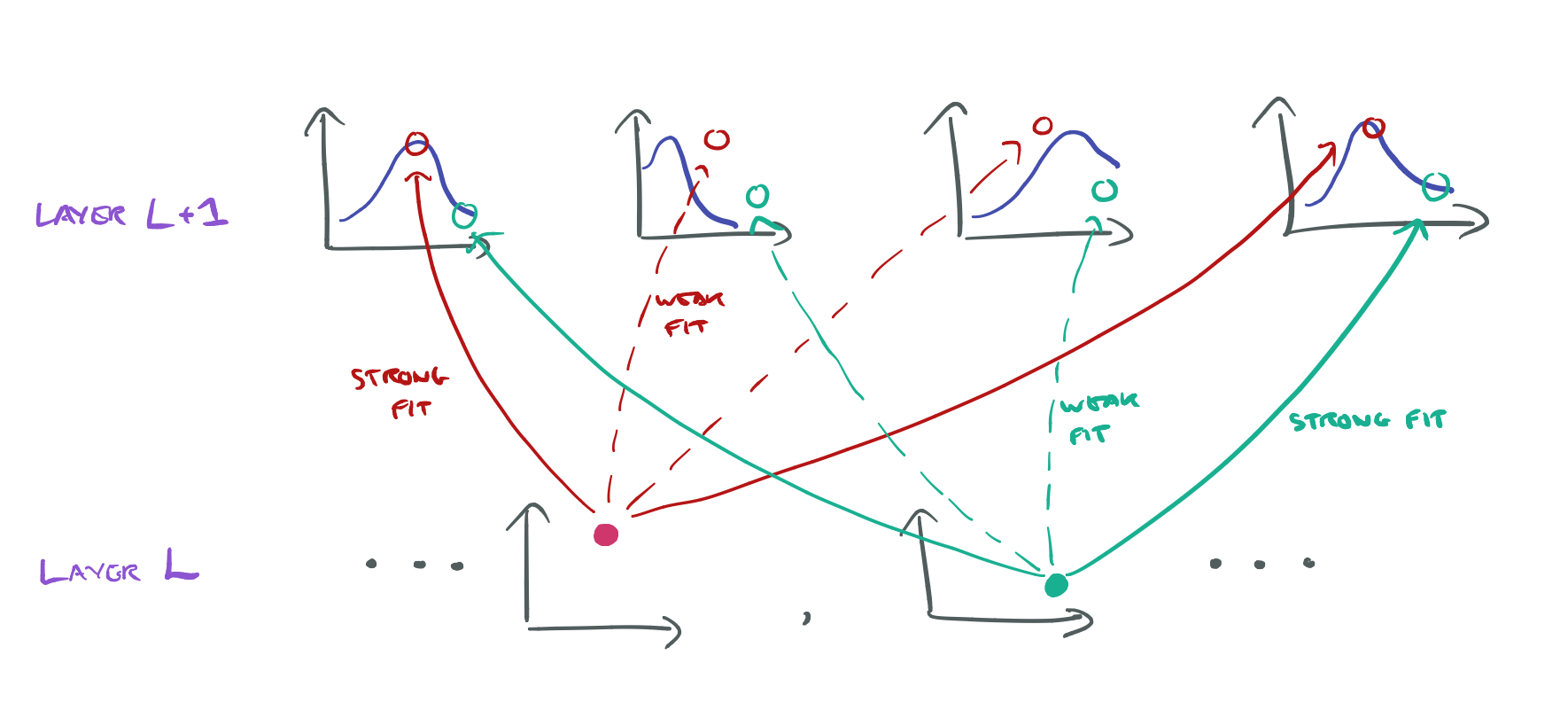
This is a standard mixture of Gaussians problem, except that we have way too many Gaussians, so we need to add a penalty that prevents us from assigning every data point to a different Gaussian.
At this point in the paper we then get a very succinct description of the routing by agreement protocol, which I can only follow at a high level, but here goes…
The cost of explaining a whole data-point
by using capsule
that has an axis-aligned covariant matrix is simply the sum over all dimensions of the cost of explaining each dimension,
of
. This is simply
where
is the probability density of the
component of the vote from
under the capsule’s Guassian model for dimension
which has variance
.
Let be the cost of summing over all lower-level capsules for a single dimension of one higher-level capsule.
The activation function of capsules is then given by:
The non-linearity implemented by a whole capsule layer is a form of cluster finding using the EM algorithm, so we call it EM Routing.
Here’s the routing algorithm in its full glory:

The overall objective function reduces a free energy function:
The recomputation of the means and variances reduces an energy equal to the squared distances of the votes from the means, weighted by assignment probabilities. The recomputation of the caspule activations reduces a free energy equal to the sum of the (scaled) costs used in the logistic function minus the entropy of the activation values. The recomputation of the assignment probabilities reduces the sum of the two energies above minus the entropies of the assignment probabilities.
A CapsNetEM network
The general architecture of a CapsNetEM network looks like this:
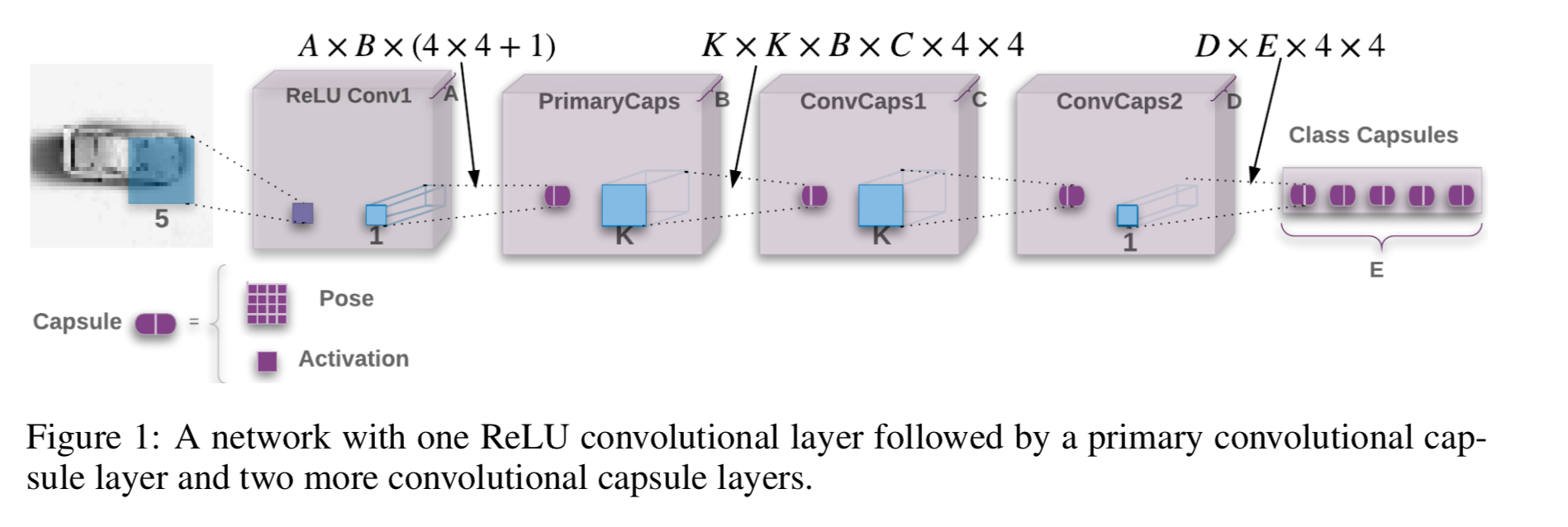
Each capsule has a 4×4 pose matrix and one logistic activation unit. The 4×4 pose of each of the primary capsules is a linear transformation of the output of all the lower layer ReLUs centred at that location. When connecting the last capsule layer to the final layer the scaled coordinate (row, column) of the centre of the receptive field of each capsule is added to the first two elements of its vote. “We refer to this technique as Coordinate Addition.” The goal is to encourage the shared final transformations to produce values for those two elements that represent the fine position of the entity relative to the centre of the capsule’s receptive field.
The routing procedure is used between each adjacent pair of capsule layers, and for convolutional capsules each capsule in layer L+1 only sends feedback to capsules within its receptive field in layer L. Instances closer to the borders of the image therefore receive fewer feedbacks.
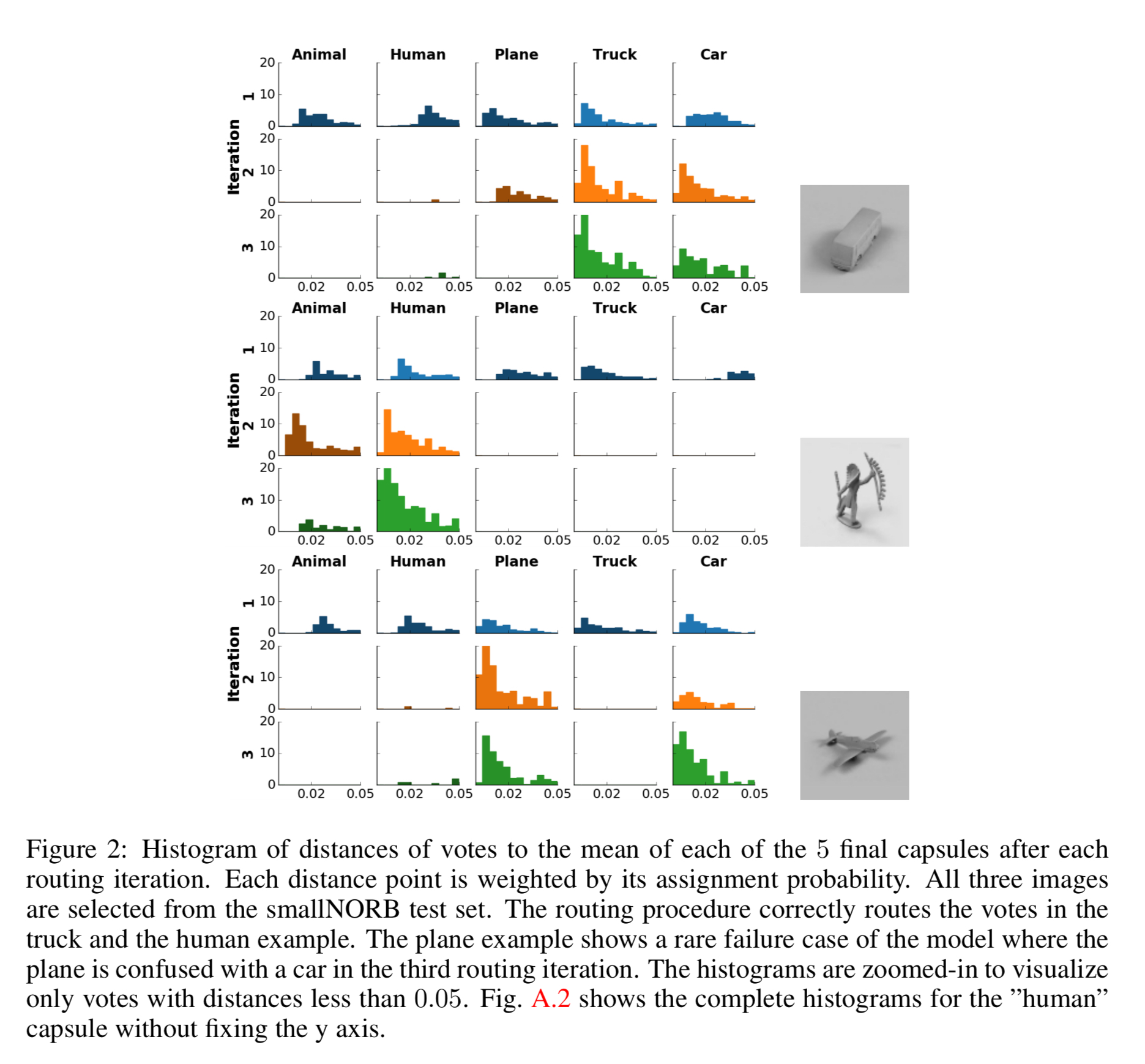
The following figure shows how the routing algorithm refines vote routing over three iterations:
CapsNetEM for smallNORB
We saw some of the results from applying CapsNetEM to smallNORB at the start of this piece. The authors also tested the ability of CapsNetEM to generalize to novel viewpoints by training both the convolution baseline and a CapsNetEM model on one third of the training data using a limited range of azimuths, and then testing on the remaining two-thirds containing the full set of azimuths. Compared with the baseline CNN, capsules with matched performance on familiar viewpoints reduce the test error rate on novel viewpoints by about 30%.
SmallNORB is an ideal data-set for developing new shape-recognition models precisely because it lacks many of the additional features of images in the wild. Now that our capsules model works well on NORB, we plan to implement an efficient version so that we can test much larger models on much larger data-sets such as ImageNet.