The O-Ring Theory of Economic Development – Kremer 1993
Something a little different today, loosely based on the paper cited above, but not a direct review of it. I’m hosting a retrospective evening for the GOTO London conference tonight and plan to share some of these ideas there…
The pursuit of excellence is no longer optional. More precisely, the pursuit of excellence across the board in your IT processes and practices is no longer optional. I came to this conclusion after reflecting on some of the 2015 State of DevOps Survey results that Nicole Forsgren shared in her recent GOTO London talk, and wondering what could explain the two-orders-of-magnitude discrepancy between the best and worst performers. The light bulb moment for me was making a connection with ‘The O-Ring Theory of Economic Development.’ I’ll explain that theory and how it fits later in this article. I love simple models with great explanatory power (for example, the USL), and O-Ring theory certainly fits the bill. Based on this, I speculate about an O-Ring Theory of DevOps that explains how even a small drop in quality levels across the board, or one or two weaker areas, can have a dramatic effect on the overall output of the organisation.
A Two Orders of Magnitude Gap
The 2015 State of DevOps survey found a 200x (two orders-of-magnitude) gap in lead times between the best and worst performers. Not just a little bit better, or 2x better, or even 20x better, but 200x! And the best performers aren’t just moving faster, they’re also delivering higher quality: 60x fewer deployment failures, and a 168x faster MTTR in the event of a failure. It seems that instead of ‘move fast and break things’ we should perhaps be talking about ‘move fast to fix things!’ Instead of trading-off between feature delivery speed and quality, it turns out that they are instead correlated. O-Ring Theory can explain both how large gaps can arise between the very best performers and the rest, and how quality and velocity are intimately related.
These differences really matter. An organisation moving 200x faster has 200x the opportunity to learn and improve based on feedback. The survey also found that the highest-performing organisations are also 2x more likely to exceed profitability, market share and productivity goals, and had a 50% higher market cap growth over 3 years.
As Barry O’Reilly touched on in his GOTO London talk, the 2015 OECD report on ‘The Future of Productivity’ also highlights a widening gap between the (business) performance of the very best and the rest. From the forward:
Productivity is the ultimate engine of growth in the global economy. Raising productivity is therefore a fundamental challenge for countries going forward…. the growth of the globally most productive firms has remained robust in the 21st century. However, the gap between those global leaders and the rest has increased over time, and especially so in the services sector.

(image credit HBR, ‘Productivity is Soaring at Top Firms and Sluggish Everywhere Else’.
… This report marks the start of a renewed and concerted effort across the OECD to put productivity at the heart of our work on strong, inclusive, and sustainable growth.
O-Ring Theory Primer
Michael Kremer published ‘The O-Ring Theory of Economic Development’ in 1993. The theory was inspired by analysis of the 1986 Challenger Shuttle disaster, where the failure of a single O-ring led to catastrophic results. For a very accessible introduction, see the following video from Tyler Cowen and Alex Tabarrok published by the Mercatus Center:
O-Ring Theory applies when the following conditions are met:
- Production depends on completing a series of tasks
- Failure or quality reduction of any one task reduces the value of the entire product
- You can’t substitute quantity for quality
As an example of the third condition, if you’re trying to produce a great meal, you can’t substitute two mediocre chefs for one great one.
Consider a production process consisting of n tasks to produce one unit of output (firms can replicate the process an arbitrary number of times). Each task is undertaken by a worker, who performs the task at some quality level q.
A worker’s skill (or quality) at a task q, is defined by the expected percentage of maximum value the product retains if the worker performs the task. Thus, a q of 0.95 could refer to a worker who has a 95% chance of performance the task perfectly and a 5% chance of performing it so badly the product is worthless, to a worker who always performs a task in such a way that the product retains 95% of its value, or to a worker who has an 50% chance of performing the task perfectly and a 50% chance of making a mistake that reduces the value of the product to 90% of its maximum possible value.
Let qi represent the quality level of the worker performing the ith task for i ∈ 1..N.
Let B be the output per worker with a single unit of capital if all tasks are performed equally.
The expected production for a single instance of the production process is then given by:
E = (q1 * q2 * … * qn) * nB
For simplicity, let’s set B=1 and n=10. Look at what happens as the quality level of the workers drops by a small amount:
| q (for all workers) | Output |
|---|---|
| 0.99 | 9.04 |
| 0.95 | 5.99 |
| 0.90 | 3.49 |
Small differences in quality produce large differences in output (and worker wages, in the economic model).
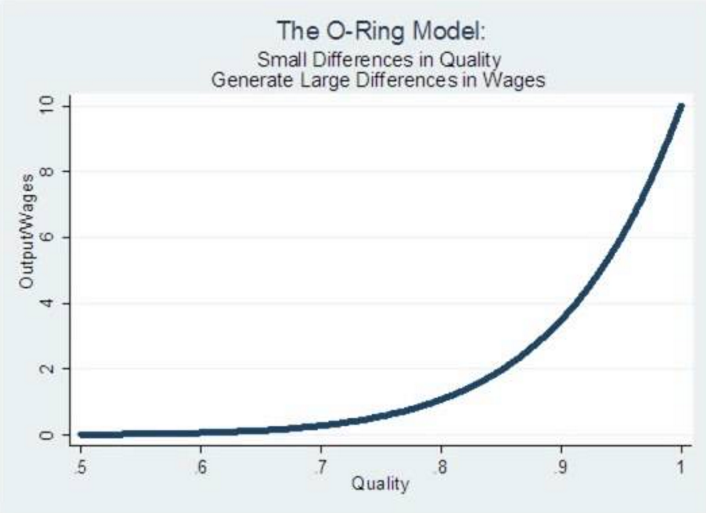
Similarly, if we have 9 outstanding workers (q=0.99), but one that is mediocre (say, q=0.5) then the output also drops dramatically to 4.57 (and with two mediocre workers and 8 great ones to 2.31).
Conversely, if we have 9 mediocre workers, and one great one, the highly skilled worker does not pull up the output very much – we get production of 0.02!
Let’s suppose we start with ten good workers (q=0.8). Let’s look at what happens to output as we train them one by one to get to great (q=0.99):
| # workers at q=0.8 | # workers at q=0.99 | output |
|---|---|---|
| 10 | 0 | 1.1 |
| 9 | 1 | 1.3 |
| 8 | 2 | 1.6 |
| 7 | 3 | 2.0 |
| 6 | 4 | 2.5 |
| 5 | 5 | 3.1 |
| 4 | 6 | 3.8 |
| 3 | 7 | 4.7 |
| 2 | 8 | 5.9 |
| 1 | 9 | 7.3 |
| 0 | 10 | 9.0 |
The more great workers a company already has, the more incremental value another great worker adds.
Applying O-Ring Theory to DevOps
Let’s now test the three O-Ring Economic Theory conditions against a DevOps pipeline, where the ‘worker’ for each stage may be a human or an automated process step. We’re looking at the production process for a single unit, e.g. a feature moving along the value stream from inception to production. The ‘value’ of our output we will consider as how quickly and accurately we can get features into production.
To test the three conditions, we’ll need to work out what ‘quality’ means for us when assessing the value of each worker. We’re interested in the velocity of features released into production, so intuitively our definition of quality should incorporate some notion of the time taken to perform the step, as well as the quality of the artefact produced by the step. Borrowing from value stream mapping, we can use the concepts of lead time and percent complete and accurate. Lead time is the elapsed time from the moment work is made available to a process step, until it is completed (and includes any queueing time and delays).
Karen Martin and Dave Ostertag explain percent complete and accurate in their book ‘Value Stream Mapping’:
Percent complete and accurate (%C&A) is the most transformational metric we’ve encountered. It reflects the quality of each process’s output. The %C&A is obtained by asking downstream consumers what percentage of the time they receive work that is ‘usable as is,’ meaning that they can do their work without having to correct the information that was provided, add missing information that should have been supplied, or clarify information that should have and could have been clearer.
For a DevOps pipeline we’ll treat %C&A as the percentage of time a downstream consumer receives an output that they can use without causing errors.
We need the quality metric for the O-Ring Theory of DevOps to be a percentage – %C&A is already in this form, but lead time isn’t. So let’s normalize lead time by comparing it against best-in-class lead time for the step in hand. That leads us to a definition of quality for step i as follows:
qi = α.%C&Ai + β.(world-class lead timei / lead timei)
α, β are simply weightings we can use to adjust the relative importance of %C&A and lead time, where α + β = 1. Note that if we produce output that is 100% complete and accurate, and do so with the same lead time as the best in the world, then quality is 1 (100%).
Finally we can make our assessment:
- Production depends on completing a series of tasks. This clearly holds for a DevOps pipeline.
- Failure or quality reduction of any one task reduces the value of the entire product. This also holds – if any one step in the process fails entirely, we get no output (the feature never makes it to production). Equally, if the quality of the ‘worker’ at a given process step is reduced (i.e. it takes a long time to perform) then the value of the entire output
- You can’t substitute quantity for quality. I spent a long time arguing forward and backward with myself over this one, and finally concluded that it does indeed hold. Remember that we’re talking about the DevOps pipeline from the perspective of a single feature moving through it. For example, running two mediocre test-suites or deployments in parallel does not improve our process quality output for the single feature over one great test-suite and deployment process. Can multiple mediocre developers outperform one great one? In the general case, Fred Brooks has shown this not to be the case…
The final aspect of this formulation is that the number of steps in a DevOps process may vary from team to team, and having more steps does not increase the value of the output. In fact, we’d like to be able to compare processes with differing numbers of steps. So let’s normalise n at 100 to give the O-Ring DevOps Metric for some DevOps pipeline p:
O-Ring(p) = 100 * (q1 * q2 * … * qn)
where
qi = α.%C&Ai + β.(world-class lead timei / lead timei)
Which will give us a nice scale from 0-100.
Implications for DevOps
If all of this speculation turns out to be correct, and the O-Ring Theory does indeed apply to DevOps pipelines, then there are some interesting consequences:
- A single weak link in your DevOps pipeline brings down your overall output dramatically. It’s not enough to be good in one or two areas and mediocre everywhere else, you need to be good (or great) across the board.
- Small differences in quality (i.e, in how quickly and accurately you perform each stage of your DevOps pipeline) quickly compound to make very large differences between the performance of the best-in-class and the rest.(Two orders of magnitude perhaps, as seen in the data from the State of DevOps Practice Survey?).
- The better you already are, the more value you get from improving your weaknesses. Conversely, if you’re fairly poor across the board, you won’t get as high a return on investment on an improvement in one specific area as a company with a higher overall level would. These forces tend to lead to ‘skill-matching’ – fairly uniform levels of performance across the board in the various steps of a DevOps pipeline for a given organisation.
If you want to be a high performing organisation, the pursuit of excellence across the board in your IT processes and practices is no longer optional.
One final observation on something that initially struck me as an oddity: if you add a stage to your DevOps pipeline, the O-Ring Theory of DevOps suggests that your overall output will tend to go down. Can this be right? If you added a stage that takes some time but adds no value, then clearly this would be correct (remember that we defined output value to be based on how quickly and accurately we could get features into production). What about adding a stage that does something useful though? This is catered for by the %C&A component: suppose the step is necessary for the downstream components to do their work (e.g. it’s a step that pushes an image to a registry, without which the next stage can’t deploy anything) – if we take it out the %C&A leading into the downstream stage will drop to 0 (broken pipeline). Now we’re clearly better off including the stage! In a more nuanced case, let’s suppose we’re talking about removing a testing phase – if that actually resulted in no drop in the %C&A of work moving through the pipeline this would in fact be a reasonable thing to do (we’d have a useless test suite). But if the %C&A of work progressing downstream did drop because of the lack of earlier testing, then once again it’s likely we’d be better of doing the testing…